в Функція косинус або cos коротко кажучи, це одна з шести Тригонометричні функції основа тригонометрії. Косинус у тригонометрії задається як відношення основи до гіпотенузи прямокутного трикутника. Функція косинуса представлена ​​як Cos x, де x – кут, для якого обчислюється відношення косинуса. З точки зору функції, ми можемо сказати, що x є вхідним значенням або областю визначення функції косинус.

Він широко використовується в широкому діапазоні предметів, таких як фізика, геометрія та інженерія, зокрема, за рахунок використання його періодичної природи. Наприклад, він використовується для визначення хвильової природи звукових хвиль, розрахунків електричного потоку через плоску поверхню тощо. У цій статті ми детально дізнаємось про те, що таке косинус, домен і діапазон функції косинус, період і графік функції косинус.

Зміст

• Що таке функція косинус?
• Cos в одиничному колі
• Графік косинусної функції
• Функція, обернена до косинуса
• Функція косинус в численні
• Тотожності функції Cos

Що таке функція косинус?

Функція косинус — це тригонометрична функція, яка за своєю природою є періодичною. Функція косинуса виражається як cos x, де x — один із гострих кутів прямокутного трикутника. Функція косинуса визначає відношення основи та гіпотенузи для заданого значення x. Функція косинуса скорочено називається cos(x) або cos(θ), де x — кут у радіанах, а тета θ — кут у ступенів загалом. Функцію косинуса можна визначити за допомогою одиничного кола, тобто кола одиничного радіуса, як ми побачимо далі в цій статті. Він має періодичний характер і повторює свої значення після кожного повного повороту кутів. На декартовій площині це можна назвати компонентою вектора гіпотенузи, паралельної осі х.

Визначення функції косинус

Функція косинуса визначається в прямокутному трикутнику як відношення довжини сторони, прилеглої до відповідного кута, до довжини гіпотенузи. Математично функція косинус задана як

Cos x = Cos θ = довжина основи/довжина гіпотенузи = b/h = OB/OA

де x кут у радіанах, а θ еквівалентний кут у градусах.

Область визначення та діапазон функції Cos

Ми знаємо, що для функції домен — це допустимі вхідні значення, а діапазон — вихідне значення для цього конкретного вхідного або доменного значення. Отже, ми можемо припустити, що функція діє як процесор, який приймає вхідні дані, обробляє їх і видає конкретний вихід. Область визначення та діапазон функції cos обговорюється нижче:

• Область визначення функції косинуса: Р тобто множина всіх дійсних чисел.
• Діапазон функції косинуса: [-1, 1], тобто результат коливається для всіх дійсних чисел від -1 до 1.

Період функції косинуса

The функція має періодичний характер, тобто повторюється через 2π або 360°. Іншими словами, вона повторюється після кожного повного оберту. Отже, період функції косинуса дорівнює повному повороту або куту 360° (або 2π).

Величина, зворотна функції косинуса

Величина, зворотна функції косинуса, відома як січна функція або сек для короткого. Математично значення, зворотне функції косинуса, задається як

3d в автокад

sec(θ) = 1/cos(θ)

Відповідно до правил Взаємні величини , якщо ми помножимо Cos x на Sec x, добуток завжди буде 1.

Графік косинусної функції

Графік функції косинуса нагадує графік функції синуса з тією основною різницею, що для x = 0 графік функції sin проходить від початку координат, тоді як при x = 0 графік функції косинуса проходить від (0, 1) на осях y. Нижче наведено графік значення функції косинуса, тобто y = cos x

Обговорені вище властивості можна побачити на графіку, як періодичний характер функції.

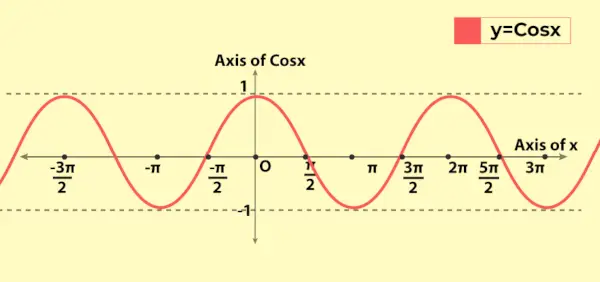
Зміна функції косинуса на графіку

Оскільки діапазон функції косинуса становить [-1, 1], тому на графіку він змінюється від -1 до 1. Він демонструє свою періодичну природу, оскільки графік повторюється після кожної довжини 2π на осі x. Це означає, що функція косинус має період 2π (або 360°).

Cos в одиничному колі

Функцію косинуса можна визначити за допомогою одиничного кола. Давайте зрозуміємо, як ми можемо визначити функцію косинус через одиничне коло.

Розглянемо відрізок OA, що обертається навколо точки O, де O є початком координат декартової площини. Таким чином, обертання OA описує одиничне коло (коло одиничного радіуса) з центром у початку координат O, і точка A завжди лежить на цьому колі. Якщо ми опустимо перпендикуляр з A на вісь x і назвемо точку перетину B, а θ — кут, який OA утворює з позитивним напрямком осі x, тоді cos(θ) = проекція гіпотенузи на x -вісь = OB/|OA| = OB (оскільки |OA| = 1 одиниця).

Зауважте, що напрямок OB є важливим, як показано на наступних малюнках. Зелений сегмент позначає довжину/величину, а стрілка позначає напрямок (+ve або -ve) cos(θ)

Зауважте, що значення cos(θ) додатне для θ, що належить до першого та четвертого квадранту, і негативне для θ, що належить до другого та третього квадранту.

Функція, обернена до косинуса

Функція, обернена до функції косинуса, відомої як арк-косинус функція і скорочено як arccos(x) або cos ^-1 (x) визначається наступним чином

cos(x) = y

⇒ cos ^-1 (y) = x

Область визначення та діапазон функції зворотного косинуса

Нижче наведено область визначення та діапазон функції зворотного косинуса:

• Область визначення функції оберненого косинуса: Усі дійсні числа в діапазоні [-1, 1]
• Діапазон функції оберненого косинуса: Усі дійсні числа в діапазоні [0, π]

Функція гіперболічного косинуса

Гіперболічні функції є аналоговим еквівалентом тригонометричних функцій, алгебраїчний вираз яких є експоненціальною функцією. Функція гіперболічного косинуса, скорочена як cosh(x) де x гіперболічний кут — поняття гіперболічної геометрії. Подібно до того, як (cos(x), sin(x)) представляє точку на одиничному колі, (cosh(x), sinh(x)) представляє точку на одиничній гіперболі, тобто xy = 1, де sinh(x) представляє гіперболічний функція синус. Алгебраїчне розкладання гіперболічної функції cos задано як

cosh(x) = (e ^x + і ^-x )/2

Детальніше про гіперболічні функції виходить за рамки цієї статті, але ви можете звернутися до них Ця стаття .

Функція косинус в численні

Розділ обчислення в математиці займається диференціація та інтеграція заданої функції. Диференціювання функції — це швидкість зміни функції відносно незалежної змінної, тоді як інтегрування — це зворотний процес диференціювання, який стосується знаходження інтеграла функції, похідна якої існує.

Похідна функції косинуса

The похідна функції косинуса дорівнює від’ємній частині функції синуса. Математично

d(cos(x))/dx = -sin(x)

Інтегрування функції косинус

The невизначений інтеграл функції косинуса дорівнює функції синуса. Математично –

∫cos(x)dx = sin(x) + C, де C – константа інтегрування.

Функції синус і косинус

Наступний графік представляє ключову різницю між функціями синус і косинус:

Різниця між функціями синус і косинус

У наступній таблиці наведено відмінності між функцією синус і косинус –

Таблиця значень Cos

У наступній таблиці наведено значення функції косинуса для деяких спільних кутів у першому квадранті декартової площини –

Ми можемо легко обчислити значення інших загальних кутів, наприклад 15°, 75°, 195°, -15° тощо, використовуючи ці значення за допомогою формул cos (x + y) і cos (x – y), описаних далі в цій статті. стаття.

перевірити, Тригонометрична таблиця

Тотожності функції Cos

Основні тригонометричні тотожності, пов’язані з функцією косинус, згадані нижче:

• без²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/сек(x)
• cos 2x = cos²x – sin²x = 1 – 2sin²х = 2cos²x – 1 = (1 – tan²х/1 + тен²x)
• cos 3x = 4cos³x – 3cos x

Схожі статті

• Диференціювання тригонометричних функцій
• Обернені тригонометричні функції
• Зворотні тригонометричні похідні

Розв'язані приклади на функцію косинус

Ось кілька розв’язаних прикладів, які допоможуть вам краще зрозуміти концепцію косинусної функції.

Приклад 1: Яке максимальне та мінімальне значення функції косинус?

рішення:

Максимальне значення функції косинуса дорівнює 1 при 0° і 180°, тоді як мінімальне значення функції дорівнює -1 при 180°.

Приклад 2: під яким кутом (кутами) в діапазоні [0, 360] значення функції косинуса дорівнює 0?

рішення:

Значення функції косинуса дорівнює 0 при кутах 90° і 270°.

Приклад 3: Для яких квадрантів значення функції косинуса є від’ємним?

рішення:

Функція косинус від'ємна в II^ndі III^rdквадранти.

Приклад 4: Обчисліть значення cos (45°).

рішення:

vlc media player завантажити youtube

Відповідно до тотожності 4, наведеної вище, cos(-x) = cos(x).

Отже, cos(-45°) = cos(45°) = 1/√2

Приклад 5: обчисліть значення cos(15°).

рішення:

Використовуючи ідентичність 3, наведену вище –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

Приклад 6: Що таке cos ^-1 (1/2) в діапазоні [0,π]?

рішення:

Нехай cos^-1(1/2) = у.

Отже, cos(y) = 1/2 ⇒ y = π/3 у наведеному вище діапазоні.

Отже, відповідь π/3.

Приклад 7: Яке значення cos(-15°)?

рішення:

Використовуючи тотожність 3, наведену вище –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Крім того, ми також можемо використати тотожність cos(-x) = cos(x) і використати значення cos(15°), обчислене в прикладі 5.

Приклад 8: обчисліть площу під графіком функції косинуса для x = 0 до x = π/2.

рішення:

Задану площу можна обчислити, розв’язавши наступний певний інтеграл –

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Отже, відповідь дорівнює 1 одиниці квадрата.

Приклад 9: якщо cos(x) = π/3, знайдіть значення cos(3x) (у десятковій формі з точністю до двох десяткових цифр).

рішення:

Використовуючи тотожність – cos(3x) = 4cos³(x) – 3cos(x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

Приклад 10: Знайдіть значення cos(120°).

рішення:

Використання тотожності для cos(2x)

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1- 2⨉(√3/2)²= 1 – 3/2 = -1/2

Практичні запитання: функції Cos

Q1. Яка формула для обчислення cos кута в прямокутному трикутнику?

Q2. Яка геометрична інтерпретація cos на декартовій площині?

Q3. Обчисліть значення cos(120°).

Q4. Знайдіть значення cos ^-1 (√3/2) в діапазоні [π, 2π].

Q5. Якщо жердина відкидає на землю тінь однакової довжини, знайдіть кут сонця до землі, якщо сонце знаходиться на сході.

Підсумок – функція косинус

Функція косинуса, позначена як cos(x), є фундаментальною тригонометричною функцією, яка визначається як відношення основи до гіпотенузи в прямокутному трикутнику та має важливе значення в різних галузях, як-от фізика, техніка та геометрія, завдяки своїй періодичній природі. , який є важливим у моделюванні хвильової поведінки. Він має домен усіх дійсних чисел і діапазон від -1 до 1, повторюючи свій цикл кожні 2 пі радіан або 360 градусів, видно з його хвилеподібного графіка, який починається з (0,1). З точки зору обчислення, похідна від cos(x) є − sin( x ), а його інтеграл дає sin( x )+ C , де C є константою інтегрування. Ця функція також поширюється на гіперболічні форми, такі як cosh(x), покращуючи її застосування в різних математичних контекстах і рішеннях, включаючи обчислення хвиль і коливань у фізичних системах.

Функція косинус: поширені запитання

1. Що таке функція косинус?

Функція косинус є однією з основних тригонометричних функцій. У прямокутному трикутнику він визначається як відношення довжини сторони, прилеглої до відповідного кута, до довжини гіпотенузи.

2. Чи тотожні косинус і косинус у тригонометрії?

Так. cos — це абревіатура/скорочена форма функції косинус.

3. Що таке діапазон функції Cos?

Діапазон функції cos або косинуса — це всі дійсні числа в діапазоні від -1 до 1, тобто [-1,1].

4. Що таке область визначення функції Cos?

Область визначення функції cos або косинуса є серією всіх дійсних чисел, тобто Р .

5. Що таке максимальне значення функції косинуса?

Максимальне значення функції косинуса дорівнює 1 для всіх кутів, еквівалентних 0° або 360°.

6. Що таке мінімальне значення функції косинуса?

Мінімальне значення функції косинуса становить -1 для всіх кутів, еквівалентних 180°.

7. Як знайти значення Cos(-x)?

Значення cos(-x) можна обчислити шляхом обчислення значення cos(x) через існування наступної тотожності: cos(-x) = cos(x).

8. Як побудувати графік функції косинуса?

Щоб накреслити графік косинусної функції на декартовій площині, візьміть вісь x кути в радіанах (або градусах), а вісь y — значення косинусної функції для відповідного кута на осі x. тепер,

• Крок 1: Візьміть підмножину осі X, для якої ви хочете намалювати графік.
• Крок 2: Розділіть вісь x у цьому діапазоні на рівновіддалені точки (тобто між усіма підточками є рівний простір). Зауважте, що чим більша кількість поділок, тим більша точність результуючого графіка.
• крок 3: Для кожної з цих підточок x позначте точку (x, cos(x)) на графіку.
• крок 4: З’єднайте всі позначені точки, щоб отримати графік функції косинуса (для вибраної вами підмножини осі х).

9. Як знайти період косинуса?

Період косинусної функції відноситься до мінімального діапазону значень, після якого функція починає повторюватися. Ми знаємо, що функція косинуса повторюється після кожного повного оберту, що означає 2π радіан. Отже, період функції косинуса дорівнює 2π радіан або 360°.

10. Що таке амплітуда косинусної функції?

Амплітуда функції косинуса відноситься до максимального зміщення значення функції від середнього положення, тобто осі x. Амплітуда функції косинуса дорівнює 1, оскільки максимальне зміщення дорівнює 1 (для значень -1 і 1 при 180 і 0 градусів відповідно. Зауважте, що діапазон функції косинуса дорівнює [-амплітуда, амплітуда].