А функція в математиці — це особливе відношення між набором вхідних значень і набором вихідних значень. У функції кожне вхідне значення дає певне вихідне значення. Ми представляємо функцію в математиці як y = f(x), де х є вхідним значенням і для кожного х ми отримуємо вихідне значення як y.

У цій статті ми дізнаємося про, функції в математиці, їх різні види, приклади та ін.

Зміст

• Що таке функція в математиці?
• Визначення функції в математиці
• Приклади функцій
• Умова для функції
• Представлення функцій у математиці
• Ідентифікація функції
• Типи функції
• Що таке функція в алгебрі?
• Область визначення та діапазон функції
• Композиція функцій
• Алгебра функцій
• Що таке функція на графіку?
• Графічні функції
• Загальні функції
• Застосування функцій
• Приклади на функції
• Практичні завдання на тему «Що таке функція».

Що таке функція в математиці?

Функція в математиці - це a відношення між вхідними значеннями (доменом) і вихідними значеннями (діапазоном) заданих наборів так, щоб жодні дві змінні з наборів доменів не були пов’язані з тією самою змінною в наборі діапазону. Простим прикладом функції в математиці є f(x) = 2x, яка визначена на R→R, тут будь-яка змінна в області пов’язана лише з однією змінною в діапазоні.

Функція в математиці має область визначення, кодобласть і діапазон. Область визначення — це множина всіх можливих значень x, а діапазон функції — це множина всіх вихідних значень y. Діапазон — це підмножина кодомени функції. Ми також можемо сказати, що функція в математиці — це відношення з унікальним виходом, і жодні два вхідних значення не мають подібних виходів у функції, що стосується відношення.

Визначення функції в математиці

Функція — це спеціальне відношення або метод, що з’єднує кожен член множини A з унікальним членом множини B через визначене відношення. Множину A називають областю визначення, а множину B — співобластю функції. Функція в математиці від множини A до множини B визначається як,

f = ∀ a ∈ A, b ∈ B

Кожна функція є відношенням, але кожне відношення не є функцією. Критерії того, що будь-яке відношення вважається функцією, оскільки у функції кожен елемент множини A має лише одне зображення в множині B, тоді як у відношенні елемент множини A може мати більше одного зображення в множині B.

Ми визначаємо функції в математиці від непорожньої множини A до непорожньої множини B так, що,

(a, b) ∈ f, то f(a) = b

куди ми дзвонили b як образ a визначений у відношенні f .

Кожен елемент 'а' множини A має єдине зображення ' b у множині B, то це функція.

Приклади функцій

Функція в математиці f визначається як y = f(x), де х є вхідним значенням, і для кожного вхідного значення x ми отримуємо унікальне значення y. Різні приклади функцій у математиці, визначених на R→R:

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+ 3 і т.д

Умова для функції

Для будь-яких двох непорожніх множин A і B функція f: A→B означає, що f є функцією від A до B, де А є доменом і Б є співдоменом.

Для будь-якого елемента a ∈ A існує єдиний елемент b ∈ B такий, що (a,b) ∈ f. Унікальний елемент b, пов'язаний з a, позначається f(a) і читається як f з a. Це краще зрозуміти із зображення нижче:

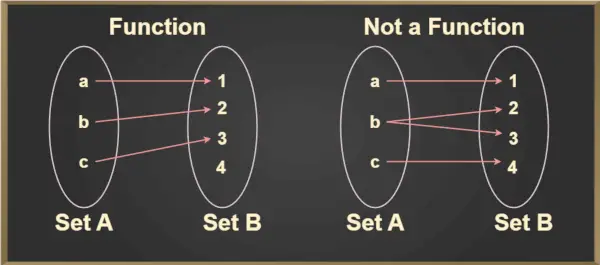
Тест вертикальної лінії

Тест вертикальної лінії використовується, щоб визначити, чи є крива функцією чи ні. Якщо будь-яка крива перерізає вертикальну лінію в більш ніж одній точці, то крива не є функцією.

Представлення функцій у математиці

Ми представляємо функцію в математиці як,

y = f(x) = x + 3

Тут набір значень x є областю визначення функції, а набір вихідних значень y є співобластю функції. Тут функція визначена для всіх дійсних чисел, оскільки вона дає унікальне значення для кожного x, але не завжди можливо отримати результат для кожного значення x, у такому випадку ми визначаємо функцію з двох частин, це можна розуміти як

• f(x) = 1/(x – 2), де x ≠ 2
• f(x) = x²де x ∈ {R}

Ми можемо визначити функцію в математиці як машину, яка приймає деякі вхідні дані та дає унікальний результат. Функція f(x) = x²визначається нижче як,

Ми можемо представити функцію в математиці за допомогою трьох методів, як,

• Набір впорядкованих пар
• Форма таблиці
• Графічна форма

Наприклад, якщо ми представимо функцію як f(x) = x³

Інший спосіб представлення тієї самої функції – як набір впорядкованих пар як,

f = {(1,1), (2,8), (3,27)}

У вищезазначеному наборі область визначення функції дорівнює D = {1, 2, 3}, а діапазон функції дорівнює R = {1, 8, 27}

Ідентифікація функції

Функція класифікується як особливий тип відношення в математиці. Існують наступні правила, за якими можна ідентифікувати функцію:

• Відношення, у якому кожен вхід зіставляється з унікальним виходом, є функцією. Це називається функцією один до одного.
• Відношення, у якому два входи (прообрази), зіставлені з одним виходом, також є функцією. Це багато до однієї функції.
• Відношення, в якому один вхід відображається на два різних виходу, не є функцією.
• Відношення, у якому багато вхідних даних зіставляються з багатьма виходами за жодним певним правилом, не є функцією.

Типи функції

Інший Типи функцій використовуються для вирішення різних типів математичних задач, особливо пов'язаних з кривими та рівняннями. У математиці існує три основні типи функцій, які базуються на відображенні елементів із множини A на множину B.

Ін'єктивна функція або функція один до одного

Функція, у якій кожен елемент домену має окреме зображення в кодомене, називається Ін'єктивний або Функція «один до одного». .

f: A → B називається взаємним або ін’єктивним, якщо зображення різних елементів A під f є різними, тобто

підрядок рядок java

f(a ₁ ) = b ₁ , f(a ₂ ) = b ₂

де₁, а₂∈ A і b₁, б₂∈ B

Сюр'єктивні функції або Онто-функції

Сюр'єктивна функція — це функція, у якій кожен елемент кодомени має прообраз у домені. Його також називають На функцію це означає, що кожен елемент codomain пов’язаний з кожним елементом домену. Жоден елемент codomain не повинен мати порожнє відношення. Кількість елементів кодомена і діапазону однакова.

f: A → B називається onto, якщо кожен елемент B є образом деякого елемента A під f, тобто для кожного b ϵ B існує елемент 'a' в A такий, що f(a) = b.

Бективна функція

Якщо функція має властивості як ін’єктивної (один до одного), так і сюр’єктивної (на функцію), то ця функція називається Бективна функція . У біективній функції кожен елемент домену пов’язаний з кожним елементом кодомена, а також існує відношення один до одного. Це означає, що кількість елементів кодомена та діапазону однакова, і жоден елемент ні в домені, ні в кодомене не має порожнього відношення.

На основі вихідних значень функції класифікуються як парні та непарні. Давайте подивимося на них

Непарні функції

Непарна функція — це тип функції, яка демонструє симетрію щодо початку координат. Зокрема, якщо f(x) є непарною функцією, вона показує, що f(-x) = -f(x)

Навіть функція

Парна функція — це тип функції, яка демонструє симетрію відносно осі y. Зокрема, якщо f(x) є парною функцією, вона показує, що f(-x) = f(x)

Що таке функція в алгебрі?

Функція в алгебра це рівняння, для якого будь-який x, який можна ввести в рівняння, дасть рівно один результат, наприклад y, з рівняння. Він представлений як y = f(x), де x — незалежна змінна, а y — залежна змінна.

Наприклад:

• y = 2x + 1
• y = 3x – 2
• y = 4y
• y = 5/x

Область визначення та діапазон функції

Домен і діапазон функції є вхідним і вихідним значенням функції відповідно. Наприклад, скажімо, у нас є функція, задана як f(x) = x². Тут ми можемо взяти все дійсне число як вхідне значення x, а на виході завжди буде позитивне дійсне число. Отже, його область визначення — це набір усіх дійсних чисел, представлених як R, а його діапазон — набір додатних дійсних чисел, представлених як R⁺

Композиція функцій

Якщо f: A → B і g: B → C дві функції. Тоді композиція f і g позначається як f(g) і визначається як функція туман = f(g(x)) для x ∈ A.

Візьмемо дві функції f(x) = x + 3 і g(x) = 2x²

туман = f(g(x))

⇒ туман = f(2x²)

⇒ зуб = 2x²+ 3

Вивчайте більше, Композиція функції

Алгебра функцій

Алгебра функцій передбачає алгебраїчні операції, що виконуються між двома функціями. Нижче наведено алгебраїчну операцію для двох функцій f(x) і g(x), визначених для дійсного значення x:

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {Оскільки k — дійсне число}
• (f/g)(x) = f(x) /g(x); {Для g(x) ≠ 0}

Що таке функція на графіку?

Функцію можна легко представити на графіку. Будь-яка функція на графіку представляє криву (включно з прямою лінією) у площині x-y, відображену для її вхідних і відповідних вихідних значень.

Щоб побудувати графік функції на a, спочатку знайдіть кілька точок, які лежать на функції, а потім з’єднайте ці точки відповідно до геометричного місця функції. Наприклад, щоб побудувати графік функції (пряма) f(x) = y = 5x – 2, нам потрібна якась точка на графіку. Щоб знайти точку на графіку, ми спочатку беремо випадкові значення x, а потім знаходимо відповідні їм значення y, як,

f(x) = y = 5x-2

якщо x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

якщо x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

якщо x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Тепер, об’єднавши ці точки, ми можемо отримати графік функції y = 5x – 2

Графічні функції

Знання значень x дозволяє зобразити функцію f(x) на графіку. Оскільки y = f(x), ми можемо знайти відповідне значення для y, починаючи зі значень x. У результаті ми можемо побудувати графік у координатній площині, використовуючи значення x і y. Розглянемо такий сценарій:

Припустимо, що y = x + 3

Коли x = 0, y = 3

Так само

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

У результаті ми можемо побудувати графік для функції x + 3, використовуючи ці значення.

Загальні функції

Деякі загальні функції, які зазвичай використовуються в математиці, обговорюються нижче:

Справжня функція

Реальна функція у математиці означає функцію, область визначення та діапазон якої є підмножинами дійсних чисел (позначаються як ℝ). Простіше кажучи, дійсна функція — це математичне правило або співвідношення, яке присвоює значення дійсного числа кожному введеному дійсному числу.

Реальні функції

Поліноміальна функція

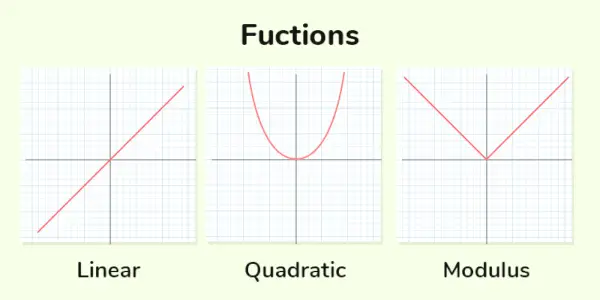
Функція, у якій показники алгебраїчних змінних є цілими невід’ємними числами, називається Поліноміальна функція . Якщо ступінь змінної дорівнює 1, вона називається лінійною функцією, якщо степень дорівнює 2, вона називається квадратичною функцією, а якщо ступінь дорівнює 3, вона називається кубічною функцією. Деякі приклади поліноміальних функцій наведено нижче:

• y = x²
• y = 2x + 3
• y = 3x³

Поліноміальна функція може бути класифікована на наступні типи:

Лінійна функція : Лінійні функції – це функції, у яких максимальна потужність змінної дорівнює 1. Загальна форма Лінійна функція є y = mx + c

Квадратична функція : Квадратична функція – це функція, у якій максимальна потужність змінної дорівнює 2. Загальна форма квадратична функція є, сокира ² + bx + c = 0

Кубічна функція : Кубічна функція це ті, у яких максимальний ступінь змінної дорівнює 3. Загальний вигляд кубічної функції подано як сокира ³ + bx ² + cx + d = 0

Обернена функція

Обернена функція це функція, що містить обернену функцію до іншої функції. Скажімо, у нас є функція y = f(x), тоді її зворотна функція буде x = f^-1(у). У y = f(x) доменом є x, а діапазоном є y, а у випадку x = f^-1(y), домен – y, а діапазон – x. Таким чином, можна сказати, що область визначення вихідної функції є областю її оберненої функції, а область визначення вихідної функції є областю визначення вихідної функції. Деякі приклади обернених функцій:

• y = так^-1(x)
• y = x^-1

Функція площі

Функція площі зазвичай відноситься до математичної функції, яка обчислює площу геометричної фігури або області. Функція area приймає один або кілька параметрів як вхідні дані та повертає площу відповідної форми. Нижче наведено деякі з функцій області:

Площа функції кола : Площа кола (A) є функцією його радіуса (r), так що,

A = πr ²

Функція площі трикутника : Площа трикутника (A) є функцією його основи (b) і висоти (h), так що,

A = (bh)/2

Експоненціальна функція

Експоненціальна функція це той, який представлений як f(x) = e^х. Його часто використовують, щоб показати швидке зростання або занепад.

Логарифмічна функція

Логарифмічна функція це математична функція, яка представляє дію, обернену до піднесення до степеня. Він представлений як f(x) = log x.

Функція стелі

Функція стелі , що позначається як ⌈x⌉, округлює дійсне число x до найближчого цілого числа, яке більше або дорівнює x. Іншими словами, він знаходить найменше ціле число, яке більше або дорівнює x.

Функція підлоги

Функція Floor, позначена як ⌊x⌋, округлює дійсне число x до найближчого цілого числа, яке менше або дорівнює x. Іншими словами, він знаходить найбільше ціле число, яке менше або дорівнює x.

Функція модуля

Модуль функції , також відома як функція абсолютного значення, повертає величину або розмір дійсного числа без урахування його знака. Модульна функція позначається як ∣x∣, де x – вхідне значення.

Функція Signum

Функція сигнум , також відома як функція знака або функція signum, — це математична функція, яка повертає знак дійсного числа. Він вказує, додатне, від’ємне чи нульове число.

Тригонометричні функції

Тригонометричні функції це математичні функції, які зв’язують кути прямокутного трикутника з довжинами його сторін. Шість основних тригонометричних функцій: синус (sin), косинус (cos), тангенс (tan), косеканс (cosec), секант (sec) і котангенс (cot).

Комплексні функції

Будь-яка функція, у якій вхідна змінна є комплексною функцією, називається комплексною функцією. Комплексне число — це число, яке можна зобразити на комплексній площині. В комплексне число ми маємо дійсне число та уявне число. Комплексне число (z) представлено у вигляді z= x + iy, а комплексна функція представлена ​​у вигляді f(z) = P(x, y) + iQ(x, y)

Застосування функцій

Коли ми говоримо, що змінна величина y є функцією змінної величини x, ми вказуємо, що y залежить від x і що значення y визначається значенням x. Цю залежність можна виразити так: f = y (x).

• Радіус кола можна використовувати для обчислення площі кола. Радіус r впливає на площу A. Ми оголошуємо, що A є функцією r математичною мовою функцій. Ми можемо записати A = f(r) =π×r²
• Об’єм кулі V є функцією її радіуса. V = f(r) = 4/3×r³позначає залежність V від r.
• Сила є функцією прискорення тіла фіксованої маси m. F = g(a) = m×a.

Люди також читають:

• Зв'язок і функція
  
• Область визначення та область тригонометричних функцій
• Діапазон функції
• Гіперболічна функція

Приклади на функції

Приклад 1. Для двох функцій f і g визначено як f(x) = x ² і g(x) = ln(2x). Знайдіть складену функцію (gof )( x )

рішення:

Дано:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln(2f (x))

= ln(2x²)

= 2 ln(√2x)

Отже, (gof)(x) = 2 ln(√2x)

Приклад 2: Знайти результат функції g(t)= 6t ² + 5 у

• (i) t = 0
• (ii) t = 2

рішення:

Дана функція,

g(t)= 6t²+ 5т

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

Приклад 3: Довжина прямокутника в п’ять разів перевищує його ширину, виразіть площу прямокутника як функцію його довжини.

рішення:

Нехай довжина прямокутника дорівнює l, а ширина прямокутника дорівнює b

тепер,

• b = l/5

Площа прямокутника (A) = l × l/5 = l²/5

Отже, площа прямокутника як функція його довжини дорівнює,

A(l) = l ² /5

Практичні завдання на тему «Що таке функція».

1. Дано функцію f(x)=3x+5

• Знайти f(2)
• Знайти f(−1)
• Визначте область визначення та область визначення функції.

2. Дано функцію g(x)=x ² – 4x + 3

що таке map java

• Знайдіть корені функції.
• Знайдіть g(3) і g(0).
• Визначте вершину функції.

3. Дано дві функції f(x)=x + 2 і h(x)=2x – 3

• Знайти складену функцію (f ∘ h) (x)
• Обчислити (f ∘ h)(2)

Резюме – Що таке функція

Функція в математиці — це спеціальне відношення між вхідними значеннями (область) і вихідними значеннями (діапазон), де кожен вхід пов’язаний з унікальним виходом. Функції, представлені як y = f(x), мають специфічні характеристики та можуть бути візуалізовані за допомогою впорядкованих пар, таблиць або графіків. Вони важливі в різних математичних задачах і бувають різних типів, включаючи ін’єктивні (один-до-одного), сюр’єктивні (onto) і біективні (обидва). Функції можна перевірити за допомогою тесту вертикальної лінії, і далі вони класифікуються на поліноміальні, обернені, експоненціальні, логарифмічні та тригонометричні функції. Розуміння функцій передбачає розпізнавання їх домену, діапазону та правил, що їх визначають. Приклади включають прості лінійні функції, такі як y = 2x + 1 і складні композиції функцій. Функції відіграють вирішальну роль в алгебрі, геометрії та численні, допомагаючи в представленні та аналізі математичних зв’язків і явищ реального світу.

Поширені запитання про те, що таке функція

Що таке визначення функції?

Відношення f, визначене на множині A до іншої множини B, називається функцією в математиці, якщо кожне значення A має унікальне значення в множині B.

Як написати функцію в математиці?

Функція f у математиці представлена ​​як f: A → B і визначається як, f(x) = x + 2. Тут для кожного унікального значення x ми маємо унікальне значення y.

Як перетворити функцію?

Ми можемо легко перетворити функцію на інші функції, просто виконуючи основні алгебраїчні операції над функцією. Різними перетвореннями функції є відображення, перенесення, обертання тощо.

Що таке раціональна функція?

Функція дробу, у якій чисельник і знаменник є поліноміальними функціями, називається раціональною функцією. Деякі приклади раціональної функції:

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), тощо

Що таке лінійна функція?

Алгебраїчна функція, у якій кожен член функції постійний або має ступінь одиниці, називається лінійною функцією. Деякі приклади лінійної функції:

• f(x) = 2x + 3
• g(x) = x – 5 тощо.

Що таке домен і кодобмен функції?

Якщо ми визначимо функцію як, y = f(x). Тоді доменом x є всі значення x, для яких y призводить до унікального значення. А співобласть y — це набір усіх значень y для кожного значення x.

Як визначити функцію в математиці?

Якщо будь-яке вхідне значення (x) домену у відношенні має більше одного зображення (y), то це відношення ніколи не може бути функцією. Отже, якщо значення x повторюється в упорядкованій парі, то воно ніколи не є функцією.