Комплексні числа є природним продовженням дійсних чисел. У сучасну епоху комплексні числа використовуються в багатьох галузях, таких як цифрова обробка сигналів, криптографія та багато пов’язаних з комп’ютером галузей.

У цій статті ми дізнаємося про уявні числа, комплексні числа та їх типи, різні операції над комплексними числами, властивості комплексних чисел, застосування комплексних чисел тощо.

Комплексні числа Означення

Комплексні числа є числа форми (a + i b) де a & b є дійсними числами і i це уявна одиниця, яка називається йотою, яка представляє √-1. Наприклад, 2 + 3i — комплексне число, у якому 2 — дійсне число, а 3i — уявне число. Комплексні числа можна записати як a + ib, де a і b — раціональні числа, які можна представити на числовій прямій, що тягнеться до нескінченність .

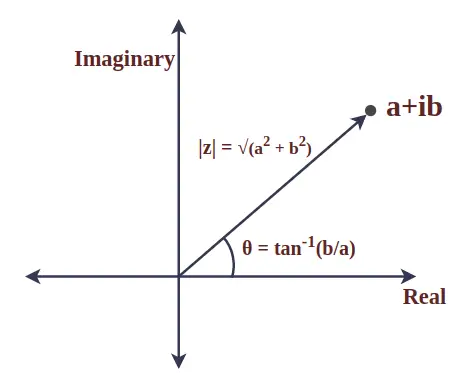
Модуль комплексного числа

Модуль комплексного числа є абсолютним значенням і представляє відстань між початком координат і заданою точкою. Він також відомий як величина комплексного числа. Давайте розглянемо комплексне число z = a + ib, тоді модуль z визначається як:

|z| = √(a ² + б ² )

де,

• a — дійсна частина комплексного числа z, а
• b є уявною частиною комплексного числа z.

Аргумент комплексного числа

Кут між радіус-вектором комплексного числа і додатною віссю х називають аргументом комплексного числа. Для комплексного числа z = a + ib воно математично визначається як:

θ = tan ^-1 (б/а)

де,

• a — дійсна частина комплексного числа z, а
• b є уявною частиною комплексного числа z.

Потужність i(йота)

I(iota) визначається як квадратний корінь з -1. Таким чином, будь-який ступінь i може бути виражений як багаторазове множення i на самого себе, тобто

подвійний в java

• i = √(-1)
• i²= -1
• i³= – я
• i⁴= 1
• i⁵= i
• i⁶= – 1
• і так далі..

Необхідність комплексних чисел

У стародавні часи люди знали лише такі натуральні числа числа є найбільш інтуїтивно зрозумілими за своєю природою, оскільки людський мозок уже розуміє їх, використовуючи візуальні зображення таких речей, як овець і їжі. Таким чином, ми маємо лише множину натуральних чисел ( Н ), але в натуральних числах немає розв’язку рівняння x + a = b (a> b) і a, b ∈ N. Таким чином, виникло розширення натуральних чисел, тобто Цілі числа ( я ).

Тепер у цьому наборі чисел немає розв’язку рівняння ax = b (a ≠ 0) і a, b ∈ I, де a і b обидва цілі числа. Таким чином, множина цілих чисел (I) розширюється до множини раціональних чисел ( Q ).

Знову ж таки, у цьому наборі раціональних чисел немає розв’язку рівняння x²= a (a> 0) і a ∈ Q. Отже, Q поширюється на такі числа, що x²= a(для a> 0) тобто ірраціональні числа. Цей набір називається дійсними числами і представлений Р .

Довгий час вважалося, що нам не потрібно розширювати цей набір дійсних чисел, щоб сформувати інший більший набір, оскільки ця колекція чисел здається повною. Але знову виникла нова проблема в цій множині чисел, тобто не існує дійсного числа такого, що x²= a (a <0) і a ∈ R. Таким чином, набір дійсних чисел розширено далі, щоб включити всі такі значущі та названі цим набором комплексними числами та представлено C .

Класифікація комплексних чисел

Як відомо, стандартна форма комплексного числа така z = (a + i b) де a, b ∈ R, а i — йота (уявна одиниця). Отже, залежно від значень a (дійсна частина) і b (уявна частина) комплексні числа поділяються на чотири типи:

• Нульове комплексне число
• Чисто дійсні числа
• Чисто уявні числа
• Уявні числа

Давайте докладніше дізнаємося про ці види.

Нульове комплексне число

Для будь-якого комплексного числа z = a + ib, якщо a = 0 & b = 0, то комплексне число називається нульовим комплексним числом. Наприклад, єдиним прикладом цього є 0.

Чисто дійсні числа

Для будь-якого комплексного числа z = a + ib, якщо a ≠ 0 & b = 0, то комплексне число називається чисто дійсним числом, тобто числом без уявної частини. Усі дійсні числа є прикладами цього, наприклад 2, 3, 5, 7 тощо.

Чисто уявні числа

Для будь-якого комплексного числа z = a + ib, якщо a = 0 & b ≠ 0, то комплексне число називається чисто уявним числом, тобто числом без дійсної частини. Усі числа без дійсних частин є прикладами цього типу чисел, наприклад, -7i, -5i, -i, i, 5i, 7i тощо.

Уявні числа

Для будь-якого комплексного числа z = a + ib, якщо a ≠ 0 & b ≠ 0, то комплексне число називається уявне число . Наприклад, (-1 – i), (1 + i), (1 – i), (2 + 3i) тощо.

Різні форми комплексних чисел

Існують різні форми комплексних чисел, які,

• Прямокутна форма
• Полярна форма
• Експоненціальна форма

Тепер дізнаємося про них докладніше.

Прямокутна форма

Прямокутна форма є також називається Стандартна форма і це представлено (a + ib), де a і b — дійсні числа.

Наприклад: (5 + 5i), (-7i), (-3 – 4i) тощо.

Полярна форма

Полярна форма це представлення комплексного числа, де полярні координати [де координати представлені як (r, θ), де r — відстань від початку координат, а θ — кут між лінією, що з’єднує точку та початок координат, і додатною віссю x) використовуються для представлення комплексного числа. Будь-яке комплексне число представляється як r [cos θ + i sin θ].

Наприклад: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6] тощо.

Експоненціальна форма

Експоненціальні форми комплексних чисел є представленням комплексних чисел за допомогою формули Ейлера, і в цій формі комплексне число представлено reⁱ, де r — відстань точки від початку координат, а θ — кут між додатною віссю x і радіус-вектором.

Наприклад: eⁱ⁽⁰⁾, Це є^i(π/2), 5.e^i(π/6)і т.д.

Примітка: Усі три форми комплексних чисел, розглянуті вище, є взаємоперетворюваними, тобто їх можна дуже легко перетворити з однієї форми в іншу.

Операції над комплексними числами

Над комплексними числами можна виконувати наступні операції:

• Доповнення
• Віднімання
• Множення
• Поділ
• Сполучення

Додавання комплексних чисел

Ми можемо скласти два комплексні числа, просто склавши їх дійсну та уявну частини окремо.

Наприклад, (3 + 2i) + (1 + 4i) = 4 + 6i.

приклади dfa

Віднімання комплексних чисел

Ми можемо відняти два комплексні числа, просто віднімаючи їх дійсну та уявну частини окремо.

Наприклад, (3 + 2i) – (1 + 4i) = 2 – 2i.

Множення комплексних чисел

Ми можемо помножити два комплексні числа, використовуючи властивість розподілу та той факт, що i²= -1.

Наприклад, (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Ділення комплексних чисел

Ми можемо поділити одне комплексне число на інше, просто помноживши чисельник і знаменник на комплексно сполучене знаменнику й далі спростивши вираз.

Наприклад, (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Сполучення комплексних чисел

Ми можемо легко знайти спряжене комплексне число, просто змінивши знак його уявної частини. Спряжене комплексне число часто позначається рискою над числом, наприклад z̄.

Наприклад, кон’югат 3 + 2i є 3 – 2i.

Тотожності для комплексних чисел

Для будь-яких двох комплексних чисел z₁і z₂можна дати такі алгебраїчні тотожності:

• (З ₁ + z ₂ ) ² = (z ₁ ) ² + (з ₂ ) ² + 2 з ₁ × z ₂
• (З ₁ - З ₂ ) ² = (z ₁ ) ² + (з ₂ ) ² – 2 з ₁ × z ₂
• (З ₁ ) ² - (З ₂ ) ² = (z ₁ + z ₂ )(З ₁ - З ₂ )
• (З ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² с ₂ +3(з ₂ ) ² с ₁ + (з ₂ ) ³
• (З ₁ - З ₂ ) ³ = (z ₁ ) ³ – 3(з ₁ ) ² с ₂ +3(з ₂ ) ² с ₁ - (З ₂ ) ³

Формули, пов’язані з комплексними числами

Існує кілька формул, пов’язаних із комплексними числами, деякі з яких:

Формула Ейлера

Формула Ейлера показує зв’язок між уявним ступенем експоненти та тригонометричним відношенням sin і cos і визначається як:

Це є ^ix = cos x + i sin x

Формула де Муавра

Формула де Муавра виражає н^тисступінь комплексного числа в полярній формі і визначається як:

(cos x + i sin x) ^п = cos(nx) + i sin(nx)

Складна площина

Площина, на якій комплексні числа однозначно представлені, називається комплексною площиною, площиною Аргана або площиною Гауса.

Комплексна площина має дві осі:

• Вісь X або реальна вісь
• Вісь Y або уявна вісь

Вісь X або реальна вісь

java колекції java

• Усі чисто дійсні комплексні числа однозначно представлені точкою на ньому.
• Дійсна частина Re(z) усіх комплексних чисел будується відносно нього.
• Ось чому вісь X також називається Реальна вісь .

Вісь Y або уявна вісь

• Усі чисто уявні комплексні числа однозначно представлені точкою на ньому.
• Уявна частина Im(z) усіх комплексних чисел будується відносно неї.
• Ось чому вісь Y також називається Уявна вісь .

Геометричне представлення комплексних чисел

Як відомо, кожне комплексне число (z = a + i b) представлено унікальною точкою p(a, b) на комплексній площині, а кожна точка на комплексній площині представляє унікальне комплексне число.

Щоб представити будь-яке комплексне число z = (a + i b) на комплексній площині, дотримуйтеся таких умов:

• Дійсна частина z (Re(z) = a) стає X-координатою точки p

• Уявна частина z (Im(z) = b) стає Y-координатою точки p

І, нарешті, z (a + i b) ⇒ p (a, b), яка є точкою на комплексній площині.

Властивості комплексних чисел

Існують різні властивості комплексних чисел, деякі з яких такі:

• Для будь-якого комплексного числа z = a + ib, якщо z = 0, то a = 0, а також b = 0.
• Для 4 дійсних чисел a, b, c і d таких, що z₁= a + ib і z₂= c + id. Якщо z₁= z₂тоді a = c і b=d.
• Додавання комплексного числа з його сполученим призводить до чисто дійсного числа, тобто z + z̄ = дійсне число.

Нехай z = a + ib,

z + z̄ = a + один + a – один

⇒ z + z̄ = 2a (що є цілком реальним)

• Добуток комплексного числа з його спряженими результатами також є чисто дійсним числом, тобто z × z̄ = дійсне число

Тоді нехай z = a + ib

z × z̄ = (a + один) × (a – один)

⇒ z × z̄= a²– я²b²

⇒ z × z̄ = a²+ б²(що цілком реально)

• Комплексні числа є комутативний під дією додавання і множення. Розглянемо два комплексних числа z₁і z₂, і потім

с ₁ +z ₂ = z ₂ +z ₁

с ₁ × z ₂ = z ₂ × z ₁

• Комплексні числа є асоціативний з діями додавання і множення. Розглянемо три комплексні числа z₁, С₂, і z₃потім

(З ₁ +z ₂ ) +z ₃ = z ₁ + (з ₂ +z ₃ )

(З ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Комплексні числа містять розподільна власність множення над додаванням також. Розглянемо три комплексні числа z₁, С₂, і z₃потім

с ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Детальніше,

• Ділення комплексних чисел
• Бар Z у комплексних числах

Приклади на комплексні числа

Приклад 1: побудуйте ці комплексні числа z = 3 + 2i на комплексній площині.

рішення:

Дано:

с = 3 + 2 і

Отже, точка z(3, 2). Тепер ми накладаємо цю точку на графік нижче, тут на цьому графіку вісь х представляє дійсну частину, а вісь у — уявну частину.

безкоштовне проти безкоштовного

Приклад 2: побудуйте ці комплексні числа z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 i), z ₄ = (1 – i) на комплексній площині.

рішення:

Дано:

с₁= (2 + 2 i)

с₂= (-2 + 3 i)

с₃= (-1 – 3 i)

с₄= (1 – i)

Отже, точки дорівнюють z₁(2, 2), z₂(-2, 3), z₃(-1, -3) і z₄(1, -1). Тепер ми наносимо ці точки на графік нижче, тут на цьому графіку вісь х представляє дійсну частину, а вісь ординат представляє уявну частину.

Поширені запитання про комплексні числа

Дайте визначення комплексних чисел.

Числа у формі a+ib називаються комплексними числами, де a і b — дійсне число, а i — уявна одиниця, яка представляє квадратний корінь з -1.

Чим дійсне число відрізняється від комплексного?

Різниця між дійсними і комплексними числами полягає в тому, що нам потрібно лише одне число для представлення будь-якого дійсного числа, але потрібні два дійсних числа для представлення будь-якого комплексного числа.

Що таке дійсна та уявна частини комплексного числа?

У комплексному числі а + ib а — дійсна частина комплексного числа, а b — уявна частина комплексного числа.

Що таке комплексне сполучення комплексного числа?

Для комплексного числа a + ib, a – ib називається його комплексно спряженим. Комплексно спряжені можна знайти, просто змінивши знак уявної частини.

Що таке модуль комплексного числа?

Відстань між початком координат і точкою, представленою комплексним числом на аргандній площині, називається модулем цього повного числа, і для z = a + ib вона математично визначається як:

|z| = √(a ² + б ² )

Що таке аргумент комплексного числа?

Кут між радіус-вектором комплексного числа та додатною віссю x називається аргументом комплексного числа, а для z = a + ib він математично визначається як:

θ = tan ^-1 (б/а)

Що таке полярна форма комплексного числа?

Для будь-якого комплексного числа z = a + ib його полярна форма визначається як:

r [cos θ + i sin θ]

Що таке формула Ейлера?

Формула Ейлера показує зв’язок між уявним ступенем експоненти та тригонометричним відношенням sin і cos і визначається як:

Це є ^ix = cos x + i sin x