- DFA відноситься до детермінованих кінцевих автоматів. Детермінований стосується унікальності обчислення. Скінченні автомати називаються детермінованими кінцевими автоматами, якщо машина зчитує вхідний рядок по одному символу за раз.
- У DFA існує лише один шлях для певного введення з поточного стану до наступного.
- DFA не приймає нульове переміщення, тобто DFA не може змінити стан без будь-якого введеного символу.
- DFA може містити кілька кінцевих станів. Він використовується в лексичному аналізі в компіляторі.
На наступній діаграмі ми можемо бачити, що від стану q0 для входу a є лише один шлях, який веде до q1. Так само, від q0, є лише один шлях для входу b, що йде до q2.
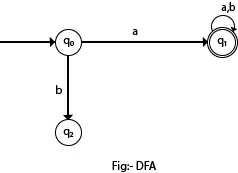
Формальне визначення DFA
DFA — це набір 5-ти кортежів, як ми описали у визначенні FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Функцію переходу можна визначити як:
δ: Q x ∑→Q
Графічне представлення DFA
DFA може бути представлений орграфами, які називаються діаграмами стану. В якому:
- Стан представлено вершинами.
- Дуга, помічена символом введення, показує переходи.
- Початковий стан позначено стрілкою.
- Кінцевий стан позначено подвійним кружечком.
приклад 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} рішення:
Діаграма переходу:

Таблиця переходів:
avl обертання дерева
| Сучасний стан | Наступний стан для входу 0 | Наступний стан введення 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
приклад 2:
DFA з ∑ = {0, 1} приймає всі, починаючи з 0.
рішення:

Пояснення:
- На наведеній вище діаграмі ми бачимо, що при заданому 0 як вхідному сигналі для DFA у стані q0 DFA змінює стан на q1 і завжди переходить до кінцевого стану q1 при початковому введенні 0. Він може приймати 00, 01, 000, 001... .і т.д. Він не може прийняти будь-який рядок, який починається з 1, тому що він ніколи не перейде до кінцевого стану на рядку, який починається з 1.
приклад 3:
DFA із ∑ = {0, 1} приймає всі, що закінчуються на 0.
оператор перемикання Java
рішення:

Пояснення:
На наведеній вище діаграмі ми можемо бачити, що при заданому 0 як вхідному сигналі для DFA у стані q0, DFA змінює стан на q1. Він може прийняти будь-який рядок, який закінчується на 0, наприклад 00, 10, 110, 100.... тощо. Він не може прийняти будь-який рядок, який закінчується на 1, оскільки він ніколи не перейде до кінцевого стану q1 на 1 вході, тому рядок, який закінчується на 1, не буде прийнято або буде відхилено.
