Кут вимірюється в градусах (°) і радіанах. Він утворюється між двома суміжними сторонами багатокутника. Кожен багатокутник має різні сторони та різну кількість кутів. Формула для знаходження кутів у градусах корисна в геометрії та тригонометрії. Важливо розуміти інші поняття математики, такі як дуга, центральний кут кола тощо.
- Повне коло = 360°
- Пряма = 180°
- Півколо = 180°
- Чверть кола = 90°
Обчислення кутів у градусах
Існує три способи визначення кутів у градусах:
- Використання протектора D
- Використання теореми Піфагора та тригонометричної функції в прямокутному трикутнику
- Використання формули суми кутів
- Центральний кут кола
Використання протектора D
Протектор — це тип лінійки або шкали, який використовується для вимірювання відстані в сантиметрах або міліметрах. Протектор, який використовується для вимірювання кутів, має форму «D» із значенням кутів, позначених від 0 до 180° з будь-якого напрямку (праворуч або ліворуч). Нам потрібно вирівняти вісь з лінією на D, щоб виміряти кут. Середнє коло протектора вирівнюється з вершиною вимірюваного кута. Промені вздовж вершини кута допоможуть знайти кут у градусах.
Використання теореми Піфагора та тригонометричної функції в прямокутному трикутнику
У тригонометрії є шість функцій, синус, cos, cosec, tan, cot, і сек. Прямокутний трикутник має три сторони: основу, перпендикуляр і гіпотенузу.
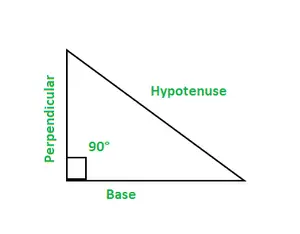
- Основа: це сторона, прилегла до кута 90°. Перпендикуляр: вона також є стороною, прилегла до кута 90°. Гіпотенуза: це сторона, протилежна куту 90°.
Одним із кутів прямокутного трикутника є кут 90°. Загальна сума кутів трикутника дорівнює 180°.
- Cosecθ: представлено як гіпотенуза, поділена на перпендикуляр.
Cosecθ =
- Cotθ: представлено як основа, поділена на перпендикуляр.
Cotθ =
Інші тригонометричні функції представлені у вигляді:
sinθ =
Cosθ =
tanθ =
секθ =
Cosecθ також може бути представлений як 1/ sinθ
secθ також можна представити як 1/ cosθ
Cotθ також можна представити як 1/tanθ
Де,
Θ – кут
Теорема Піфагора
Якщо відомі дві сторони прямокутника, ми можемо легко обчислити третю сторону прямокутного трикутника. У прямокутному трикутнику теорема Піфагора визначається так:
(гіпотенуза)2= (база)2+ (перпендикуляр)2
Формула суми кутів
Сума кутів відноситься до загальної суми внутрішніх кутів багатокутника, утвореного між двома сторонами. Якщо у багатокутника шість сторін, то навколо шести кутів. Це допомагає знайти кут, якщо відомі інші кути та сума кутів багатокутника.
Формула для обчислення загальної суми кутів многокутника має вигляд:
Загальна сума кутів = 180 (n – 2)
Де,
n — кількість сторін багатокутника
приклад:
- Якщо n = 4,

Загальна сума кутів = 180 (4 – 2)
= 180 (2)
= 360°
Якщо n = 5,
Загальна сума кутів = 180 (5 – 2)
= 180 (3)
наприклад ім'я користувача= 540°
- Якщо n = 6

Загальна сума кутів = 180 (6 – 2)
= 180 (4)
= 720°
Центральний кут кола
Коло — це фігура круглої форми, межа якої рівновіддалена від центральної точки. Відстань між центром і межею називається радіусом кола. Кут, утворений двома радіусами кола, відомий як центральний кут. Значення центрального кута кола лежить в межах від 0 до 360 градусів.

Формула для обчислення центрального кута кола визначається так:
Довжина дуги = 2πr × (θ/360)
Θ = 360л/2пр
Де,
r — радіус кола
АВ — дуга
Тета - це кут у градусах.
L = довжина дуги
Зразки завдань
Запитання 1: Знайдіть центральний кут кола радіусом 2 м із довжиною дуги 4 м?
Рішення :
Формула для обчислення центрального кута кола визначається так:
Θ = 360л/2пр
Де,
r — радіус кола
Тета - це кут у градусах.
L = довжина дуги
Θ = кут у градусах
r = 2м
L = 4м
Θ = 360 × 4 /2 × π × 2
Θ = 114,6°
Отже, центральний кут кола дорівнює 114,6°.
Запитання 2: Знайдіть центральний кут кола радіусом 10 см із довжиною дуги 18 см?
Рішення :
Формула для обчислення центрального кута кола визначається так:
Θ = 360л/2пр
пустий список javaДе,
r — радіус кола
Тета - це кут у градусах.
L = довжина дуги
r = 10 см
L = 18 см
Θ = кут у градусах
Θ = 360 × 18 /2 × π × 10
Θ = 103,13°
Отже, центральний кут кола дорівнює 103,13°.
Запитання 3. Знайдіть кут паралелограма, якщо інші три кути дорівнюють 80°, 95° і 105°?
Рішення :
У паралелограма чотири сторони, сумарна сума кутів яких дорівнює 360°.
Формула для знаходження суми кутів = 180 (n – 2)
Де,
n — кількість сторін багатокутника
Тут n = 4,
Загальна сума кутів = 180 (4 – 2)
= 180 (2)
= 360°
Загальна сума = Кут 1 + Кут 2 + Кут 3 + Кут 4
360 = 80+ 95+ 105+ Кут 4
360 = 280 + кут 4
Кут 4 = 360 – 280
Кут 4 = 80°
Завдання 4: Знайдіть кут А на даному малюнку.

Рішення :
Дано: Гіпотенуза = 12
Перпендикуляр = 6
Тригонометрична функція для обчислення кута визначається так:
sinA = 6/12
А = 30°
Завдання 5: Знайдіть кут А на даному малюнку.

Рішення :
Дано: Гіпотенуза = 10
Основа = 5
Тригонометрична функція для обчислення кута визначається так:
CosA = 5/10
А = 60°
Запитання 6. Знайдіть кут п’ятикутника, якщо інші чотири кути дорівнюють 115°, 100°, 105° і 100°?
Рішення :
У п'ятикутника п'ять сторін із сумою кутів 540°.
Формула для знаходження суми кутів = 180 (n – 2)
Де,
n — кількість сторін багатокутника
Тут n = 5,
Загальна сума кутів = 180 (5 – 2)
= 180 (3)
= 540°
Загальна сума = Кут 1 + Кут 2 + Кут 3 + Кут 4 + Кут 5
540 = 115° + 100° + 105°+100° + кут 5
540 = 420 + кут 5
Кут 5 = 540 – 420
Кут 5 = 120°
Завдання 7: Знайдіть кут А на даному малюнку.

Рішення :
Дано: основа = √3
Перпендикуляр = 1
Тригонометрична функція для обчислення кута визначається так:
tanθ =
tanθ = 1/√3
А = 30°
Запитання 8. Знайдіть кут паралелограма, якщо інші три кути дорівнюють 100°, 70° і 80°?
Рішення :
У паралелограма чотири сторони, сумарна сума кутів яких дорівнює 360°.
Формула для знаходження суми кутів = 180 (n – 2)
Де,
n — кількість сторін багатокутника
Тут n = 4,
Загальна сума кутів = 180 (4 – 2)
= 180 (2)
= 360°
Загальна сума = Кут 1 + Кут 2 + Кут 3 + Кут 4
360 = 100 + 70 + 80 + кут 4
360 = 250 + кут 4
Кут 4 = 360 – 250
Кут 4 = 110°
Отже, інший кут дорівнює 110°.
Запитання 9: Знайдіть кут шестикутника, якщо інші п’ять кутів дорівнюють 120°, 115°, 110°, 125° і 105°?
Рішення :
У шестикутнику шість сторін із загальною сумою кутів 720°.
Формула для знаходження суми кутів = 180 (6 – 2)
Де,
n — кількість сторін багатокутника
Тут n = 6,
Загальна сума кутів = 180 (6 – 2)
= 180 (4)
= 720°
Загальна сума = Кут 1 + Кут 2 + Кут 3 + Кут 4 + Кут 5 + Кут 6
720 = 120 + 115 + 110 + 125 + 105 + кут 6
720 = 575 + кут 6
файл відкрито в javaКут 6 = 720 – 575
Кут 6 = 145°
Отже, шостий кут шестикутника дорівнює 145°.






