Таблиця тригонометрії це стандартна таблиця, яка допомагає нам знайти значення тригонометричних співвідношень для стандартних кутів, таких як 0°, 30°, 45°, 60° і 90°. Це складається з усіх шести тригонометричних співвідношень: синуса, косинуса, тангенса, косеканса, секансу та котангенса.
Давайте детально ознайомимося з таблицею тригонометрії.
Зміст
проходження замовлення поштою
- Таблиця тригонометрії
- Таблиця тригонометричних функцій
- Трюк, щоб вивчити тригонометричні співвідношення
- Як запам'ятати тригонометричну таблицю
- Як створити тригонометричну таблицю
- Тригонометричні формули
- Таблиця тригонометричних тотожностей
- Приклади тригонометричних таблиць
Таблиця тригонометрії
Тригонометрична таблиця — це розташування значень усіх шести тригонометричних функцій для їхніх спільних кутів у табличній формі.
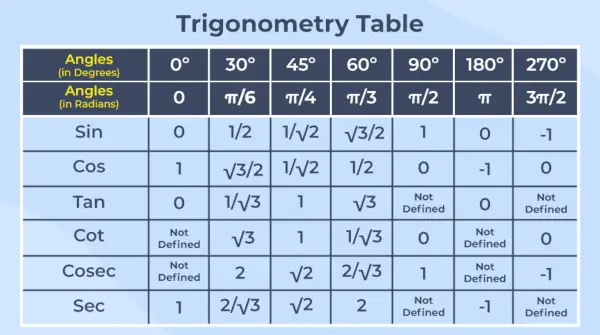
Примітка – Тригонометрія – це розділ математики, який вивчає співвідношення між кутами та сторонами прямокутного трикутника.
Таблиця тригонометричних функцій
Тригонометрія має 6 основних тригонометричних функцій: синус, косинус, тангенс, косеканс, секанс і котангенс. Тепер розглянемо тригонометричні функції.
Для будь-якого прямокутного трикутника з перпендикуляром (P), основою (B) і гіпотенузою (H) шість тригонометричних функцій є такими:
| Таблиця тригонометричних функцій | |||
| функція | Визначення | Представництво | Зв’язок зі сторонами прямокутного трикутника |
| Його | Відношення перпендикуляра і гіпотенузи | без i | Протилежна сторона / Гіпотенуза |
| Косинус | Відношення основи і гіпотенузи | cos i | Прилегла сторона / Гіпотенуза |
| Дотична | Відношення синуса і косинуса кута | так i | Протилежна сторона / Сусідна сторона |
| Косеканс | Величина, зворотна sin θ | csc i або cosec i | Гіпотенуза / Протилежна сторона |
| Січна | Величина, зворотна cos θ | сек i | Гіпотенуза / прилегла сторона |
| Котангенс | Зворотне значення tan θ | ліжечко i | Сусідня сторона / Протилежна сторона |
Примітка – Тригонометрія – це розділ математики, який вивчає співвідношення між кутами та сторонами трикутників, зокрема прямокутних. Він передбачає вивчення та застосування синуса, косинуса, тангенса та інших тригонометричних функцій для розв’язання задач у різних областях.
Перевірте : Тригонометрія: формули, таблиця, тотожності та співвідношення
Трюк, щоб вивчити тригонометричні співвідношення
Вивчіть наведену нижче таблицю, щоб легко запам’ятати тригонометричні співвідношення.
| Деякі люди мають кучеряве чорне волосся для створення краси |
| sin θ (дещо) = перпендикуляр (людей) / гіпотенуза (є) |
| cos θ (кучеряве) = основа (чорний) / гіпотенуза (волосся) |
| tan θ (до) = перпендикуляр (виробництво) / основа (краса) |
Як запам'ятати тригонометричну таблицю
Таблицю тригонометрії досить легко запам'ятати, якщо знати всі формули тригонометрії. Існує також трюк, який називається трюк однією рукою вивчити напам'ять таблицю тригонометрії.

Крок 1: На малюнку вище для таблиці синусів порахуйте пальці на лівій стороні стандартного кута.
крок 2: Розділіть кількість пальців на лівій стороні (обчисліть на 1-му кроці) на 4
крок 3: Знайдіть квадратний корінь із значення, обчисленого на кроці 2.
перевірити: Тригонометричні формули – список усіх тригонометричних тотожностей і формул
Як створити тригонометричну таблицю
Вивчіть наступні кроки, щоб створити тригонометричну таблицю для стандартних кутів.
Крок 1: Створіть таблицю
Створіть таблицю та перелічіть усі кути, наприклад 0°, 30°, 45°, 60° і 90°, у верхньому рядку. У першу колонку введіть усі тригонометричні функції sin, cos, tan, cosec, sec і cot.
Крок 2: Оцініть значення для всіх кутів функції sin.
Щоб знайти значення функції sin, розділіть 0, 1, 2, 3 і 4 на 4 і візьміть під корінь кожне значення відповідно як,
Для, значення sin 0° = √(0/4) = 0
Так само
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1
| без 0° | без 30° | без 45° | без 60° | без 90° |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
крок 3: Оцініть значення для всіх кутів функції cos
Значення функції cos протилежне значенню функції sin, тобто cos 0° = sin 90°, cos 30° = sin 60° і cos 45° = sin 45°, тому
| cos 0° | cos 30° | cos 45° | cos 60° | cos 90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
Крок 4: Оцініть значення для всіх кутів функції tan
Значення функції tan дорівнює функції sin, поділеній на функцію cos, тобто tan x = sin x / cos x. Значення всіх кутів у функції tan обчислюється як:
tan 0°= sin 0° / cos 0° = 0/1 = 0, аналогічно
| тому 0° | тому 30° | тому 45° | тому 60° | тому 90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | Не визначений |
Крок 5: Оцініть значення для всіх кутів функції cosec
Значення функції cosec дорівнює зворотній величині функції sin. Значення cosec 0° отримують, беручи величину, зворотну sin 0°
cosec 0° = 1 / sin 0° = 1 / 0 = не визначено. Так само
| cosec 0° | cosec 30° | cosec 45° | cosec 60° | cosec 90° |
|---|---|---|---|---|
| Не визначений | 2 | √2 | 23 | 1 |
Крок 6: Оцініть значення для всіх кутів функції sec
Значення функції sec дорівнює зворотній величині функції cos. Значення sec 0° отримують, беручи величину, зворотну cos 0°
sec 0° = 1 / cos 0° = 1 / 1 = 1. Подібним чином,
| сек 0° | сек 30° | сек. 45° | сек 60° | сек 90° |
|---|---|---|---|---|
| 1 | 23 | √2 | 2 | Не визначений |
Крок 7: Оцініть значення для всіх кутів функції ліжечка
Значення функції cot дорівнює зворотній величині функції tan. Значення cot 0° отримується шляхом взяття зворотного значення tan 0°
ліжечко 0° = 1 /загар 0° = 1 / 0 = Не визначено. Так само
| ліжечко 0° | ліжечко 30° | ліжечко 45° | ліжечко 60° | ліжечко 90° |
|---|---|---|---|---|
| Не визначений | √3 | 1 | 1/√3 | 0 |
Таким чином ми можемо створити наступну таблицю тригонометричних співвідношень:
| Тригонометрична таблиця градусів і радіанів | |||||||
|---|---|---|---|---|---|---|---|
| Кут (в градусах) | Кут (у радіанах) | без | Cos | Так | Cosec | розд | дитяче ліжечко |
| 0° | 0 | 0 | 1 | 0 | Невизначено | 1 | Невизначено |
| 30° | стор/6 | 1/2 | √3/2 | 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | √3 | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | Невизначено | 1 | Невизначено | 0 |
Тригонометричні формули
Давайте дізнаємося про деякі тригонометричні формули, пов’язані з додатковими та додатковими кутами.
- Додаткові кути: Пара кутів, сума яких дорівнює 90°
- Додаткові кути: Пара кутів, сума яких дорівнює 180°
перевірити: Тригонометричні співвідношення
Тригонометричні тотожності додаткових кутів
Тотожність додаткових кутів базується на співвідношенні між тригонометричними функціями двох кутів, які в сумі дорівнюють 90 градусам (або π/2 радіан). Вони відомі як співфункціональні тотожності .
| Тригонометрична функція | Ідентичність |
|---|---|
| Його | sin(90°− i )=cos i |
| Косинус | cos(90°− i )=без i |
| Дотична | загар (90°− i )=ліжечко i |
| Котангенс | ліжечко (90°− i )=так i |
| Січна | сек (90°− i )=csc i |
| Косеканс | cosec(90°− i )=сек i |
Тригонометричні тотожності додаткових кутів
Тотожність додаткових кутів пов’язана з тригонометричними функціями двох кутів, які в сумі дорівнюють 180 градусам (або π радіан).
| Тригонометрична функція | Ідентичність |
|---|---|
| Його | sin(180°− i )=без i |
| Косинус | cos(180°− i )=−cos i |
| Дотична | загар (180°− i )=−tan i |
| Котангенс | ліжечко (180°− i )=−ліжечко i |
| Січна | сек (180°− i )=−сек i |
| Косеканс | cosec(180°− i )=cosec i |
Таблиця тригонометричних тотожностей
Тригонометричні тотожності це тотожності, які широко використовуються при розв’язуванні тригонометричних задач. Існують різні тригонометричні тотожності, але три основні тригонометричні тотожності:
| Таблиця тригонометричних тотожностей | |
| Тригонометрична тотожність | Формула |
| Ідентичність Піфагора | без2θ + cos2θ = 1 |
| Тотожність секанс-тангенс | сек2θ – отже2θ = 1 |
| Тотожність косеканс-котангенс | cosec2θ – ліжечко2θ = 1 |
Також перевірте:
- Тригонометричні співвідношення
- Зворотні тригонометричні тотожності
- Висота і відстань
Приклади тригонометричних таблиць
Давайте розв’яжемо кілька завдань за тригонометричною таблицею.
Приклад 1: якщо sin θ = 4/5, знайдіть усі тригонометричні значення.
рішення:
Ось ми маємо,
список програм pythonsin θ = 4/5
як, sin θ = перпендикуляр / гіпотенуза
тому ми маємо перпендикуляр (P)= 4 і гіпотенузу (H) = 5
Отже, згідно з теоремою Піфагора Х 2 = П 2 +Б 2
Давайте дізнаємося значення основи (B)
52= Б2+ 42
25 = Б2+ 16
25 -16 = Б2
Б2= 9
B = 3Тепер ми маємо,
Sin θ = перпендикуляр/гіпотенуза
= AB/AC = 4/5Косинус θ = основа/гіпотенуза
= BC/AC = 3/5Тангенс θ = перпендикуляр/основа
= AB/BC = 4/3Косеканс θ = гіпотенуза/перпендикуляр
= AC/AB = 5/4Сіканс θ = гіпотенуза/основа
= AC/BC = 5/3протоколи канального рівняКотангенс θ = основа/перпендикуляр
= BC/AB = 3/4
Приклад 2: Знайдіть значення cos 45° + 2 sin 60° – tan 60°.
рішення:
З таблиці тригонометрії,
cos 45° = 1/√2, sin 60° = √3/2 і tan 60° = √3
Таким чином,
cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
Приклад 3: Знайдіть значення cos 75°.
рішення:
ми це знаємо,
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2.
Висновок – Тригонометрична таблиця
Таблиця тригонометрії надає вичерпну довідкову інформацію про тригонометричні функції синус, косинус, тангенс, косеканс, секанс і котангенс, а також їхні відповідні значення для різних кутів. я t служить цінним інструментом для вирішення тригонометричні рівняння, аналіз геометричних співвідношень і розуміння поведінки періодичних явищ. Чи в математики, фізики, інженерії чи інших галузей, тригонометрична таблиця допомагає в обчисленнях, вирішенні задач і візуалізації, сприяючи глибшому розумінню тригонометричних концепцій та їх застосування в сценаріях реального світу.
Таблиця тригонометрії – поширені запитання
Що таке тригонометрія?
Тригонометрія - це розділ математики, який вивчає кут і сторони будь-якого трикутника.
Що таке тригонометрична таблиця?
Тригонометрична таблиця — таблиця, яка містить значення всіх шести тригонометричних функцій для спільних кутів.
Хто винайшов таблицю тригонометрії?
Грецький астроном Гіппарх (127 р. до н. е.) винайшов тригонометричну таблицю.
Що таке стандартні кути в тригонометричній таблиці?
Стандартними кутами в тригонометричній таблиці є 0°, 30°, 45°, 60° і 90°.
Яке значення засмаги 45 градусів?
Значення tan 45 градусів дорівнює 1.
Як вивчити таблицю тригонометрії?
Хитрість вивчення тригонометричної таблиці така:
- Ви повинні вивчити всі значення всіх кутів функції sin.
- Значення всіх кутів функції cos є дзеркальним відображенням функції sin.
- Значення функції tan можна обчислити шляхом ділення функції sin на функцію cos.
- Значення функції cosec є зворотним sin.
- Аналогічно, sec і cot є зворотними величинами cos і cot.
Які шість основних функцій тригонометричної таблиці?
Шість основних тригонометричних функцій у тригонометричній таблиці: синус, косинус, тангенс, секанс, котангенс і косеканс.
Чи існують калькулятори, які можуть замінити тригонометричні таблиці?
Наукові калькулятори можуть обчислити тригонометричні співвідношення для будь-якого кута8.
Для чого потрібна таблиця тригонометрії?
Таблиця тригонометрії в основному використовується для знаходження значень усіх тригонометричних співвідношень для всіх кутів. Ці значення мають ряд застосувань у реальному житті.
