Одиничне коло – це коло, радіус якого дорівнює 1. Центр одиничного кола знаходиться в початку координат (0,0) на осі. The окружність одиничного кола дорівнює 2π одиниць, тоді як площа одиничного кола становить π одиниць2. Він містить усі властивості Circle. Одиничне коло має рівняння x2+ і2= 1. Це одиничне коло допомагає визначити різні тригонометричні концепції.
Одиничне коло
Одиничне коло часто позначається як S1узагальненням до вищих вимірів є одинична сфера. Давайте детальніше розберемося з одиничним колом, формулою та розв’язаними прикладами нижче.
Що таке одиничне коло?
Одиничне коло – це коло, радіус якого дорівнює одній (1) одиниці. Ми використовуємо декартову площину, щоб намалювати одиничне коло, а одиничне коло є поліномом 2-го ступеня з двома змінними. Одиничне коло має різні застосування в тригонометрії та алгебрі та в основному використовується для знаходження значень різних тригонометричних співвідношень, таких як sin x, cos x, tan x тощо.
Визначення одиничного кола
У математиці ми визначаємо одиничне коло як геометричне місце фіксованої точки, яка знаходиться на відстані однієї одиниці від центру кола. Одиничне коло має радіус одиниці, тому його називають одиничним колом.
Рівняння одиничного кола
Ми знаємо, що рівняння будь-якого кола з центром (h, k) і радіусом «r» таке:
(x – h) 2 + (y – k) 2 = r 2
Для одиничного кола ми знаємо, що r дорівнює 1 одиниці, тому рівняння одиничного кола таке:
(x – h) 2 + (y – k) 2 = 1
Формула одиничного кола
Якщо центром одиничного кола є початок координат, тобто (h, k) = (0, 0), то рівняння одиничного кола має такий вигляд:
x 2 + і 2 = 1
На зображенні нижче представлено одиничне коло з координатами центру h, k, а коли коло знаходиться в початку координат, значення h і k дорівнюють нулю, а радіус AP дорівнює 1 одиниці.
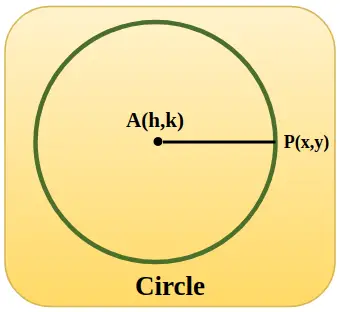
Тригонометричні функції з використанням одиничного кола
Застосування теореми Піфагора в одиничному колі краще використовувати для розуміння тригонометричних функцій. Для цього розглянемо прямокутний трикутник, розміщений всередині одиничного кола в декартовій координатній площині. Якщо зауважимо, радіус цього кола позначає гіпотенузу прямокутного трикутника.
Радіус кола утворює вектор. Це призводить до утворення кута, скажімо, θ з позитивною віссю x. Припустимо, що x — довжина основи, а y — довжина висоти прямокутного трикутника відповідно. Крім того, координати кінцевих точок радіус-вектора дорівнюють (x, y) відповідно.
Прямокутний трикутник містить сторони 1, x і y відповідно. Тепер можна обчислити тригонометричне співвідношення наступним чином:
sin θ = висота/гіпотенуза = y/1
cos θ = основа/гіпотенуза = x/1
рядок до цілого
тепер,
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Підставивши значення θ, можна отримати головні значення всіх тригонометричних функцій. Аналогічно знаходять значення тригонометричних функцій при різних значеннях.
Одиничне коло з Sin Cos і Tan
Будь-яка точка на одиничному колі з координатами (x, y) представлена за допомогою тригонометричних тотожностей як (cosθ, sinθ). Координати радіусних кутів являють собою косинус і синус значень θ для конкретного значення θ і лінії радіуса. Маємо cos θ = x і sin θ = y. Є чотири частини кола, кожна з яких лежить в одному квадранті, утворюючи кути 90°, 180°, 270° і 360°. Значення радіуса знаходяться в межах від -1 до 1 відповідно. Крім того, значення sin θ і cos θ лежать між 1 і -1 відповідно.
Одиничне коло та тригонометричні тотожності
Тригонометричні тотожності одиничного кола для котангенса, секансу та косеканса можна обчислити за допомогою тотожностей для sin, cos і tan. Остаточно отримуємо прямокутний трикутник зі сторонами 1, x і y відповідно. Обчислення тотожностей одиничного кола можна виразити так:
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- сек θ = 1/х
- cosec θ = 1/y
- cot θ = x/y
Діаграма одиничного кола
Діаграма одиничного кола — це діаграма, яка містить значення тригонометричної функції синуса та косинуса для різних кутів. Діаграма одиничного кола для того ж додана нижче,
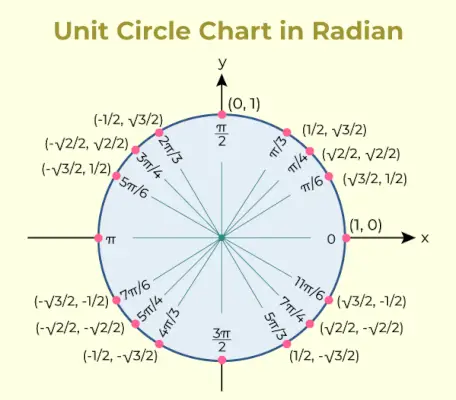
Таблиця одиничного кола
Тригонометричні співвідношення, які використовуються в таблиці одиничного кола, використовуються для переліку координат точок на одиничному колі, які відповідають спільним кутам.
| Кути | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| без | 0 | 1/2 | 1/√(2) перетворити char на рядок | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| так | 0 | 1/√(3) | 1 | √(3) мій живий цвіркун | Не визначений |
| csc | Не визначений | 2 | √(2) | 23) | 1 |
| сек | 1 | 23) | √(2) | 2 | Не визначений |
| ліжечко | Не визначений | √(3) | 1 | 1/√(3) | 0 |
Одиничні кола Піфагора
Існує три тотожності Піфагора, і всі вони легко доводяться за допомогою концепції одиничного кола. Три тотожності Піфагора є,
- без2θ + cos2θ = 1
- 1 + так2θ = сек2i
- 1 + дитяче ліжечко2θ = cosec2i
Одиничне коло Комплексна площина
Комплексні числа і комплексну площину легко пояснити за допомогою поняття одиничного кола. Рівняння одиничного кола в комплексній формі таке:
|z| = 1
gimp видалення фонуАБО
x 2 + і 2 = 1
У формі Ейлера комплексне число представлено як
z = e це = cos t + i(sin t)
Детальніше
Розв’язані приклади на одиничному колі
Q1: Доведіть, що точка Q лежить на одиничному колі, Q = [1/√(6), √4/√6]
рішення:
враховуючи,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Рівняння одиничного кола таке:
x2+ і2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Отже, точка Q[1/√(6), √4/√6] не лежить на одиничному колі.
Q2: Обчисліть так 30 О використовуючи значення sin і cos одиничного кола.
рішення:
tan 30°, використовуючи значення sin і cos,
tan 30° = (sin 30°)/ (cos 30°)
- без 30° = 1/2
- cos 30° = √(3)/2
tan 30° = 1/2/√(3)/2
цикл for у сценарії оболонкиtan 30° = 1/√(3)
Q3: Перевірте, чи лежить точка P [1/2, √(3)/2] на одиничному колі.
рішення:
враховуючи,
P = [1/2, √(3)/2]
- х = 1/2
- y = √(3)/2
Рівняння одиничного кола таке:
- x2+ і2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Практичні запитання на Unit Circle
Q1. Перевірте, чи лежать точки А (1/2, 3/2) на одиничному колі.
Q2. Перевірте, чи лежать точки A (2, 1/2) на одиничному колі.
Q3. Знайдіть значення cos 240°
Q4. Знайдіть значення tan 320°
Q5. Знайдіть значення sin 160°
Unit Circle – поширені запитання
Що таке одиничне коло?
Одиничне коло визначається як розташування точки на відстані однієї одиниці від фіксованої точки. Він має центр у (0,0), а значення його радіуса дорівнює 1.
Як перевірити, чи лежить точка на одиничному колі?
Будь-яка точка, що лежить у двовимірній площині, яка має форму (x, y), поміщається в рівняння одиничного кола x2+ і2= 1, щоб перевірити, чи лежить він на колі чи ні.
Яка формула одиничного кола?
Формула одиничного кола — це формула, яка використовується для алгебраичного представлення одиничного кола. Формула одиничного кола задається як
x 2 + і 2 = 1
Чому це називається одиничним колом?
Одиничне коло називається одиничним колом, тому що його радіус дорівнює одній (1) одиниці.
