Сильно пов'язані компоненти (SCC) є фундаментальним поняттям у теорії графів і алгоритмах. В орієнтованому графі a Сильно зв'язаний компонент це підмножина вершин, де кожна вершина в підмножині доступна з будь-якої іншої вершини в тій самій підмножині шляхом проходження спрямованих ребер. Пошук SCC графа може надати важливу інформацію про структуру та зв’язок графа із застосуваннями в різних сферах, таких як аналіз соціальних мереж, веб-сканування та мережева маршрутизація . У цьому підручнику буде розглянуто визначення, властивості та ефективні алгоритми для ідентифікації сильно пов’язаних компонентів у структурах даних графа.
bfs проти dfs
Зміст
- Що таке міцно зв’язані компоненти (SCC)?
- Чому сильно зв’язані компоненти (SCC) важливі?
- Різниця між підключеними та міцно пов’язаними компонентами (SCC)
- Чому звичайний метод DFS не можна використовувати для пошуку сильно зв’язаних компонентів?
- З’єднання двох сильно пов’язаних компонентів односпрямованим ребром
- Підхід грубої сили для пошуку міцно пов’язаних компонентів
- Ефективний підхід для пошуку сильно зв’язаних компонентів (SCC)
- Висновок
Що таке міцно зв’язані компоненти (SCC)?
А сильно зв'язаний компонент орієнтованого графа — це максимальний підграф, у якому кожна пара вершин взаємно досяжна. Це означає, що для будь-яких двох вузлів A і B у цьому підграфі існує шлях від A до B і шлях від B до A.
Наприклад: Наведений нижче граф має два компоненти сильного зв’язку {1,2,3,4} та {5,6,7}, оскільки існує шлях від кожної вершини до кожної іншої вершини в тому самому компоненті сильного зв’язку.

Сильно зв'язаний компонент
Чому сильно зв’язані компоненти (SCC) важливі?
Розуміння SCC має вирішальне значення для різних застосувань, таких як:
- Аналіз мережі : Ідентифікація кластерів тісно взаємопов’язаних вузлів.
- Оптимізація веб-сканерів : визначення тісно пов’язаних частин веб-графіку.
- Вирішення залежностей : У програмному забезпеченні, розуміння того, які модулі є взаємозалежними.
Різниця між пов’язаними та міцно пов’язаними компонентами ( SCC)
Підключення в a неорієнтований граф відноситься до того, чи є дві вершини досяжними одна від одної чи ні. Дві вершини називаються з’єднаними, якщо між ними існує шлях. Тим часом Сильно пов'язаний застосовується лише до орієнтовані графи . Підграфом орієнтованого графа вважається an Сильно пов'язані компоненти (SCC) тоді і тільки тоді, коли для кожної пари вершин А і Б , існує шлях із А до Б і шлях від Б до А . Давайте подивимося, чому стандартний метод dfs для пошуку підключених компонентів у графі не можна використовувати для визначення сильно зв’язаних компонент.
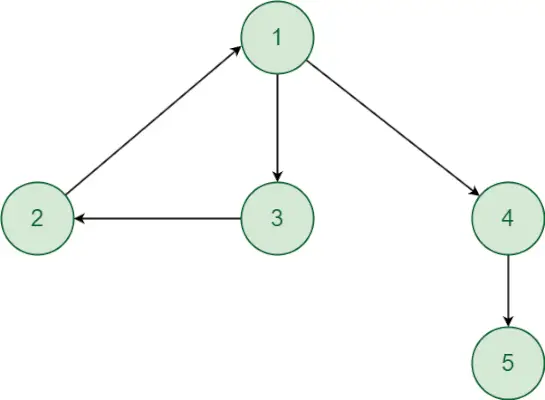
Розглянемо наступний графік:
Тепер давайте почнемо a dfs виклик із вершини 1 для відвідування інших вершин.
Чому звичайний метод DFS не можна використовувати для пошуку сильно зв'язаних компонентів?
Усі вершини можна досягти з вершини 1. Але вершини 1 і 5, 6, 7 не можуть бути в одній сильно зв’язній компоненті, оскільки немає спрямованого шляху від вершини 5, 6 або 7 до вершини 1. Граф має два сильно зв’язних компоненти. зв’язні компоненти {1,2,3,4} і {5,6,7}. Таким чином, звичайний метод dfs не можна використовувати для пошуку сильно зв’язаних компонентів.
вирівнювання тексту css
З’єднання двох сильно пов’язаних компонентів односпрямованим ребром
Два різних зв’язаних компоненти стають одним компонентом, якщо додається ребро між вершиною одного компонента до вершини іншого компонента. Але це не так у сильно зв’язаних компонентах. Два міцно зв’язані компоненти не стають одним міцно зв’язаним компонентом, якщо існує лише односпрямований край від одного SCC до іншого SCC.
симетрична різниця

Підхід грубої сили для пошуку міцно пов’язаних компонентів
Простий метод полягає в тому, щоб для кожної вершини i (яка не є частиною жодного сильного компонента) знаходити вершини, які будуть частиною сильно зв’язного компонента, що містить вершину i. Дві вершини i та j будуть в одній компоненті сильного зв’язку, якщо в них існує спрямований шлях від вершини i до вершини j і навпаки.
Розберемо підхід на наступному прикладі:
- Починаючи з вершини 1. Існує шлях від вершини 1 до вершини 2 і навпаки. Так само існує шлях від вершини 1 до вершини 3 і навпаки. Отже, вершини 2 і 3 будуть у тому самому сильно зв’язаному компоненті, що й вершина 1. Хоча існує спрямований шлях від вершини 1 до вершини 4 і вершини 5. Але немає спрямованого шляху від вершини 4,5 до вершини 1, тому вершина 4 і 5 не буде в тому самому сильно зв’язаному компоненті, що й вершина 1. Таким чином, вершини 1, 2 і 3 утворюють сильно зв’язаний компонент.
- Для Вершини 2 і 3 уже визначено сильно зв’язаний компонент.
- Для Вершини 4 існує шлях від вершини 4 до вершини 5, але немає шляху від вершини 5 до вершини 4. Таким чином, вершини 4 і 5 не будуть в одному і тому ж сильно зв’язаному компоненті. Таким чином, Вершина 4 і Вершина 5 будуть частиною Єдиного сильно зв’язаного компонента.
- Отже, буде 3 сильно пов’язані компоненти {1,2,3}, {4} і {5}.
Нижче наведено реалізацію вищезазначеного підходу:
C++ #include using namespace std; class GFG { public: // dfs Function to reach destination bool dfs(int curr, int des, vector>& присл., вектор & vis) { // Якщо поточний вузол є місцем призначення, повертає істину if (curr == des) { повертає істину; } vis[curr] = 1; for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true; } } } повертає false; } // Щоб дізнатися, чи є шлях від джерела до // призначення bool isPath(int src, int des, vector>& adj) { вектор vis(adj.size() + 1, 0); return dfs(src, des, adj, vis); } // Функція для повернення всіх сильно зв’язаних // компонентів графа. вектор> findSCC(int n, вектор>& a) { // Зберігає всі міцно пов’язані компоненти. вектор> ans; // Зберігає інформацію про те, чи є вершина частиною будь-якого // сильно пов’язаного компонентного вектора is_scc(n + 1, 0); вектор> adj(n + 1); для (int i = 0; i< a.size(); i++) { adj[a[i][0]].push_back(a[i][1]); } // Traversing all the vertices for (int i = 1; i <= n; i++) { if (!is_scc[i]) { // If a vertex i is not a part of any SCC // insert it into a new SCC list and check // for other vertices whether they can be // thr part of thidl ist. vector scc; scc.push_back(i); для (int j = i + 1; j<= n; j++) { // If there is a path from vertex i to // vertex j and vice versa put vertex j // into the current SCC list. if (!is_scc[j] && isPath(i, j, adj) && isPath(j, i, adj)) { is_scc[j] = 1; scc.push_back(j); } } // Insert the SCC containing vertex i into // the final list. ans.push_back(scc); } } return ans; } }; // Driver Code Starts int main() { GFG obj; int V = 5; vector> ребра{ { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } }; вектор> ans = obj.findSCC(V, краї); cout<< 'Strongly Connected Components are:
'; for (auto x : ans) { for (auto y : x) { cout << y << ' '; } cout << '
'; } }> Java import java.util.ArrayList; import java.util.List; class GFG { // dfs Function to reach destination boolean dfs(int curr, int des, List> присл., Список vis) { // Якщо curr вузол є призначенням return true if (curr == des) { return true; } vis.set(curr, 1); for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true; } } } повертає false; } // Щоб дізнатися, чи є шлях від джерела до // пункту призначення boolean isPath(int src, int des, List> adj) { Список vis = новий ArrayList(adj.size() + 1); для (int i = 0; i<= adj.size(); i++) { vis.add(0); } return dfs(src, des, adj, vis); } // Function to return all the strongly connected // component of a graph. List> findSCC(int n, Список> a) { // Зберігає всі міцно зв’язані компоненти. Список> ans = новий ArrayList(); // Зберігає інформацію про те, чи є вершина частиною будь-якого // сильно пов’язаного списку компонентів is_scc = новий ArrayList(n + 1); для (int i = 0; i<= n; i++) { is_scc.add(0); } List> adj = новий ArrayList(); для (int i = 0; i<= n; i++) { adj.add(new ArrayList()); } for (List edge : a) { adj.get(edge.get(0)).add(edge.get(1)); } // Обхід усіх вершин для (int i = 1; i<= n; i++) { if (is_scc.get(i) == 0) { // If a vertex i is not a part of any SCC // insert it into a new SCC list and check // for other vertices whether they can be // the part of this list. List scc = новий ArrayList(); scc.add(i); для (int j = i + 1; j<= n; j++) { // If there is a path from vertex i to // vertex j and vice versa, put vertex j // into the current SCC list. if (is_scc.get(j) == 0 && isPath(i, j, adj) && isPath(j, i, adj)) { is_scc.set(j, 1); scc.add(j); } } // Insert the SCC containing vertex i into // the final list. ans.add(scc); } } return ans; } } public class Main { public static void main(String[] args) { GFG obj = new GFG(); int V = 5; List> edges = new ArrayList(); edges.add(новий ArrayList(List.of(1, 3))); edges.add(новий ArrayList(List.of(1, 4))); edges.add(новий ArrayList(List.of(2, 1))); edges.add(новий ArrayList(List.of(3, 2))); edges.add(новий ArrayList(List.of(4, 5))); Список> ans = obj.findSCC(V, краї); System.out.println('Точно пов'язані компоненти:'); для (Список x : ans) { for (int y : x) { System.out.print(y + ' '); } System.out.println(); } } } // Цей код створено shivamgupta310570>
Python class GFG: # dfs Function to reach destination def dfs(self, curr, des, adj, vis): # If current node is the destination, return True if curr == des: return True vis[curr] = 1 for x in adj[curr]: if not vis[x]: if self.dfs(x, des, adj, vis): return True return False # To tell whether there is a path from source to destination def isPath(self, src, des, adj): vis = [0] * (len(adj) + 1) return self.dfs(src, des, adj, vis) # Function to return all the strongly connected components of a graph. def findSCC(self, n, a): # Stores all the strongly connected components. ans = [] # Stores whether a vertex is a part of any Strongly Connected Component is_scc = [0] * (n + 1) adj = [[] for _ in range(n + 1)] for i in range(len(a)): adj[a[i][0]].append(a[i][1]) # Traversing all the vertices for i in range(1, n + 1): if not is_scc[i]: # If a vertex i is not a part of any SCC, insert it into a new SCC list # and check for other vertices whether they can be part of this list. scc = [i] for j in range(i + 1, n + 1): # If there is a path from vertex i to vertex j and vice versa, # put vertex j into the current SCC list. if not is_scc[j] and self.isPath(i, j, adj) and self.isPath(j, i, adj): is_scc[j] = 1 scc.append(j) # Insert the SCC containing vertex i into the final list. ans.append(scc) return ans # Driver Code Starts if __name__ == '__main__': obj = GFG() V = 5 edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ] ans = obj.findSCC(V, edges) print('Strongly Connected Components are:') for x in ans: for y in x: print(y, end=' ') print() # This code is contributed by shivamgupta310570> C# using System; using System.Collections.Generic; class GFG { // dfs Function to reach destination public bool Dfs(int curr, int des, List> присл., Список vis) { // Якщо вузол curr є місцем призначення, повертає true if (curr == des) { return true; } vis[curr] = 1; foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true; } } } повертає false; } // Щоб дізнатися, чи існує шлях від джерела до місця призначення public bool IsPath(int src, int des, List> adj) { var show = новий список (adj.Count + 1); для (int i = 0; i< adj.Count + 1; i++) { vis.Add(0); } return Dfs(src, des, adj, vis); } // Function to return all the strongly connected components of a graph public List> FindSCC(int n, Список> a) { // Зберігає всі міцно пов’язані компоненти var ans = new List>(); // Зберігає інформацію про те, чи є вершина частиною будь-якого сильно зв’язаного компонента var isScc = new List (n + 1); для (int i = 0; i< n + 1; i++) { isScc.Add(0); } var adj = new List>(n + 1); для (int i = 0; i< n + 1; i++) { adj.Add(new List ()); } для (int i = 0; i< a.Count; i++) { adj[a[i][0]].Add(a[i][1]); } // Traversing all the vertices for (int i = 1; i <= n; i++) { if (isScc[i] == 0) { // If a vertex i is not a part of any SCC // insert it into a new SCC list and check // for other vertices whether they can be // the part of this list. var scc = new List (); scc.Add(i); для (int j = i + 1; j<= n; j++) { // If there is a path from vertex i to // vertex j and vice versa, put vertex j // into the current SCC list. if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj)) { isScc[j] = 1; scc.Add(j); } } // Insert the SCC containing vertex i into // the final list. ans.Add(scc); } } return ans; } } // Driver Code Starts class Program { static void Main(string[] args) { GFG obj = new GFG(); int V = 5; List> edges = новий список> { новий список { 1, 3 }, новий список { 1, 4 }, новий список { 2, 1 }, новий список { 3, 2 }, новий список { 4, 5 } }; Список> ans = obj.FindSCC(V, краї); Console.WriteLine('Точно пов'язані компоненти:'); foreach (var x in ans) { foreach (var y in x) { Console.Write(y + ' '); } Console.WriteLine(); } } } // Цей код створено shivamgupta310570>
Javascript class GFG { // Function to reach the destination using DFS dfs(curr, des, adj, vis) { // If the current node is the destination, return true if (curr === des) { return true; } vis[curr] = 1; for (let x of adj[curr]) { if (!vis[x]) { if (this.dfs(x, des, adj, vis)) { return true; } } } return false; } // Check whether there is a path from source to destination isPath(src, des, adj) { const vis = new Array(adj.length + 1).fill(0); return this.dfs(src, des, adj, vis); } // Function to find all strongly connected components of a graph findSCC(n, a) { // Stores all strongly connected components const ans = []; // Stores whether a vertex is part of any Strongly Connected Component const is_scc = new Array(n + 1).fill(0); const adj = new Array(n + 1).fill().map(() =>[]); для (нехай i = 0; i< a.length; i++) { adj[a[i][0]].push(a[i][1]); } // Traversing all the vertices for (let i = 1; i <= n; i++) { if (!is_scc[i]) { // If a vertex i is not part of any SCC, // insert it into a new SCC list and check // for other vertices that can be part of this list. const scc = [i]; for (let j = i + 1; j <= n; j++) { // If there is a path from vertex i to // vertex j and vice versa, put vertex j // into the current SCC list. if (!is_scc[j] && this.isPath(i, j, adj) && this.isPath(j, i, adj)) { is_scc[j] = 1; scc.push(j); } } // Insert the SCC containing vertex i into the final list. ans.push(scc); } } return ans; } } // Driver Code Starts const obj = new GFG(); const V = 5; const edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ]; const ans = obj.findSCC(V, edges); console.log('Strongly Connected Components are:'); for (let x of ans) { console.log(x.join(' ')); } // This code is contributed by shivamgupta310570> Вихід
Strongly Connected Components are: 1 2 3 4 5>
Часова складність: O(n * (n + m)), оскільки для кожної пари вершин ми перевіряємо, чи існує шлях між ними.
Допоміжний простір: O(N)
Кет Тімпф юрист
Ефективний підхід для пошуку сильно зв’язаних компонентів (SCC)
Щоб знайти SCC на графіку, ми можемо використати такі алгоритми, як Алгоритм Косараджу або Алгоритм Тар'яна . Давайте вивчимо ці алгоритми крок за кроком.
1. Алгоритм Косараджу :
Алгоритм Косараджу складається з двох основних етапів:
- Виконання пошуку в глибину (DFS) на вихідному графіку :
- Спочатку ми виконуємо DFS на вихідному графіку та записуємо час завершення вузлів (тобто час, коли DFS закінчує повне дослідження вузла).
- Виконання DFS на транспонованому графі :
- Потім ми змінюємо напрямок усіх ребер у графіку, щоб створити транспонований графік.
- Далі ми виконуємо DFS на транспонованому графіку, розглядаючи вузли в порядку зменшення часу їх завершення, записаного на першому етапі.
- Кожен обхід DFS на цьому етапі дасть нам один SCC.
Ось спрощена версія алгоритму Косараджу:
- DFS на вихідному графіку : Запис часу закінчення.
- Транспонувати графік : перевернути всі краї.
- DFS на транспонованому графі : обробіть вузли процесу в порядку зменшення часу завершення, щоб знайти SCC.
2. Алгоритм Тар'яна :
Алгоритм Тар’яна ефективніший, оскільки він знаходить SCC за один проход DFS, використовуючи стек і деяку додаткову бухгалтерію:
- Обхід DFS : Під час DFS підтримуйте індекс для кожного вузла та найменший індекс (значення нижнього посилання), який можна отримати з вузла.
- Стек : Відстежуйте вузли, які зараз знаходяться в стеку рекурсії (частина поточного SCC, що досліджується).
- Ідентифікація SCC : коли значення нижнього посилання вузла дорівнює його індексу, це означає, що ми знайшли SCC. Висувайте всі вузли зі стеку, поки не досягнемо поточного вузла.
Ось спрощена схема алгоритму Тар’яна:
- Ініціалізувати
index>до 0. - Для кожного невідвіданого вузла виконайте DFS.
- Встановіть індекс вузла та значення нижнього посилання.
- Помістіть вузол у стек.
- Для кожного сусіднього вузла або виконайте DFS, якщо він не відвіданий, або оновіть значення нижнього посилання, якщо воно є в стеку.
- Якщо значення нижнього зв’язку вузла дорівнює його індексу, витягніть вузли зі стеку, щоб сформувати SCC.
Висновок
Розуміння і знаходження сильно зв'язані компоненти в орієнтованому графі необхідний для багатьох застосувань в інформатиці. Косараю і Тар'яна Алгоритми є ефективними способами ідентифікації SCC, кожен з яких має власний підхід і переваги. Опанувавши ці поняття, ви зможете краще аналізувати та оптимізувати структуру та поведінку складних мереж.