Багатокутник в математиці це двовимірна фігура, що складається з прямих ліній, які утворюють замкнутий багатокутний ланцюг. Слово багатокутник походить від слів poly і gon, що означає багато і сторони.
Багатокутники можуть бути простими або такими, що перетинаються між собою. Простий багатокутник не перетинає сам себе, за винятком спільних кінцевих точок послідовних сегментів. Багатокутний ланцюг, який перетинає сам себе, створює багатокутник, що перетинає себе. Багатокутники також можна класифікувати як увігнуті та опуклі.
У цій статті ми докладно згадали про багатокутники та їх типи, формули та приклади.
| Важливі факти про багатокутники | |
|---|---|
| Сума внутрішніх кутів многокутника | (n–2) × 180° |
| Кількість діагоналей у багатокутнику | n(n–3)/2 |
| Внутрішній кут правильного многокутника | {(n–2) × 180°}/n |
| Зовнішній кут правильного многокутника | 360°/n |
Зміст
- Що таке багатокутники?
- Багатокутна діаграма на основі кількості сторін
- Властивості багатокутників
- Фігури багатокутників
- Типи багатокутників
- Формули багатокутників
- Кути в многокутниках
- поширені запитання
Що таке багатокутники?
Термін «многокутник» походить від грецького слова polugonos, де «poly» означає «багато», а «gon» означає «кут». Загалом, багатокутник — це замкнута фігура, утворена прямими лініями, внутрішні кути яких утворюються ними лінії. Щоб скласти замкнуту фігуру, необхідно мінімум трьох лінійних сегментів. Він широко відомий як трикутник або трикутник. Загальний термін для n-стороннього багатокутника – n-кутник.
Визначення багатокутника
Багатокутники це плоскі двовимірні фігури, що складаються з прямих сторін, які утворюють повністю закриту форму. У геометрії багатокутник — це плоска фігура, яка складається з відрізків, з’єднаних у замкнутий багатокутний ланцюг. Вони складаються з прямих сторін, а не кривих, і можуть мати будь-яку кількість сторін. Деякі багатокутники різних типів: відкриті, лише межі, замкнуті та самопересічні.
У геометрії багатокутник визначається як замкнута двовимірна фігура, що лежить на площині й оточена прямими сторонами.
Багатокутник не має вигнутих сторін, а його ребра є прямими сегментами, що визначають його межі. Точки зустрічі цих ребер називаються вершинами або кутами.
Приклади багатокутників
З точки зору математики трикутники, шестикутники, п’ятикутники та чотирикутники є прикладами багатокутників. Реальними прикладами Polygon є прямокутний екран вашого ноутбука, телевізора, мобільного телефону; прямокутне футбольне поле або майданчик, Бермудський трикутник і єгипетські піраміди трикутної форми.

Частини багатокутника
Багатокутник складається з трьох основних компонентів:
- Сторони багатокутника: Сторони багатокутників — це межі багатокутників, які визначають замкнуту область.
- Вершини: Точка, в якій зустрічаються дві сторони, називається вершиною.
- Кути: Багатокутник містить як внутрішні, так і зовнішні кути. Внутрішній кут утворюється в замкнутій області багатокутника перетином його сторін.
Багатокутна діаграма на основі кількості сторін
Номенклатура багатокутників визначається на основі кількості сторін, які вони мають. Його позначають як n-кутники, де «n» означає кількість сторін. Багатокутники зазвичай ідентифікуються за кількістю їхніх ребер. Наприклад, багатокутник із п’ятьма сторонами називається 5-кутником, а багатокутник із десятьма сторонами – 10-кутником.
| Багатокутна діаграма | ||||
|---|---|---|---|---|
| Назви фігур багатокутників | Кількість сторін | Кількість вершин | Кількість діагоналей | Міра внутрішнього кута для правильної форми |
| Трикутник | Многокутники з 3 сторонами | 3 | 0 | 60° |
| Чотирикутник | Багатокутники з 4 сторонами | 4 | 2 історія версій android | 90° |
| П'ятикутник | Многокутники з 5 сторонами | 5 | 5 | 108° |
| Шестикутник | Многокутники з 6 сторонами | 6 | 9 | 120° |
| семикутник | Многокутники з 7 сторонами | 7 | 14 | 128,571° |
| Восьмикутник | Многокутники з 8 сторонами | 8 | двадцять | 135° |
| Нонагон | Многокутники з 9 сторонами | 9 | 27 | 140° |
| Десятикутник | Многокутники з 10 сторонами | 10 | 35 | 144° |
| Гендекагон | Многокутники з 11 сторонами | одинадцять | 44 | 147,273° |
| Дванадцятикутник | Многокутники з 12 сторонами | 12 | 54 | 150° |
Властивості багатокутників
Властивості багатокутників легко ідентифікують їх. Наступні властивості допомагають легко знати багатокутники:
- Багатокутник - це замкнута форма, позбавлена відкритих кінців. Початкова та кінцева точки мають бути однаковими.
- Він має плоску форму, що складається з відрізків або прямих ліній, які разом формують фігуру.
- Як двовимірна сутність багатокутник існує лише в розмірах довжини та ширини, без глибини чи висоти.
- Він має три або більше сторін, щоб зробити багатокутник.
- Кути в багатокутнику можуть бути різними. Він демонструє чітку конфігурацію.
- Довжина сторін багатокутника може бути різною; він може бути рівним, а може і не бути рівним по всьому багатокутнику.
Фігури багатокутників
Багатокутник — це плоска двовимірна фігура, яка характеризується прямими сторонами, з’єднаними в замкнуту фігуру. Приклади багатокутників:
- Трикутник
- Чотирикутник
- П'ятикутник
- Шестикутник
- семикутник
- Восьмикутник
- Нонагон
- Десятикутник
Трикутник
- Він має 3 сторони і 3 вершини.
- Він не має діагоналей.
- Сума внутрішнього кута становить 180°.
Чотирикутник
- Він має 4 сторони і 4 вершини.
- Має 2 діагоналі.
- Сума внутрішніх кутів дорівнює 360°.
П'ятикутник
- Він має 5 сторін і 5 вершин.
- Має 5 діагоналей.
- Сума внутрішніх кутів дорівнює 540°.
Шестикутник
- Він має 6 сторін і 6 вершин.
- Має 9 діагоналей.
- Сума внутрішніх кутів дорівнює 720°.
семикутник
- Він має 7 сторін і 7 вершин.
- Має 14 діагоналей.
- Сума внутрішніх кутів дорівнює 900°.
Восьмикутник
- Він має 8 сторін і 8 вершин.
- Має 20 діагоналей.
- Сума внутрішніх кутів дорівнює 1080°.
Нонагон
- Він має 9 сторін і 9 вершин.
- Має 27 діагоналей.
- Сума внутрішніх кутів дорівнює 1260°.
Десятикутник
- Він має 10 сторін і 10 вершин.
- Має 35 діагоналей.
- Сума внутрішнього кута дорівнює 1440°.
Типи багатокутників
Залежно від сторін і кутів багатокутники можна класифікувати на різні типи за різними ознаками, наприклад:
- На основі сторін
- На основі кутів
- На підставі кордону
Многокутники на основі сторін
Залежно від характеристик сторін багатокутники можна розділити на два основні типи:
- Правильний многокутник
- Неправильний многокутник
Правильний многокутник
Правильний многокутник відрізняється тим, що всі його сторони мають однакову довжину та всі внутрішні кути однакових розмірів. Він може бути як рівностороннім, так і рівнокутним. Прикладами правильних багатокутників є трикутник, чотирикутник, п’ятикутник і шестикутник.

Правильний многокутник
Неправильний многокутник
Неправильний многокутник має різну довжину сторін і кутів різної міри. Будь-який багатокутник, який не відповідає критеріям правильного багатокутника, класифікується як неправильний. Поширеними прикладами неправильного багатокутника є масштабний трикутник, чотирикутники, такі як прямокутник, трапеція або повітряний змій, а також структури неправильного п’ятикутника та шестикутника.
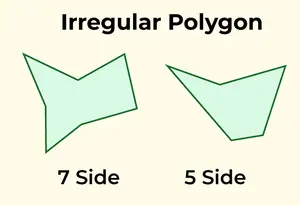
Неправильний многокутник
Многокутники на основі кутів
Багатокутники можна класифікувати за характером їхніх кутів на дві основні категорії:
- Опуклий многокутник
- Увігнутий многокутник
Опуклий многокутник
Опуклий многокутник не має внутрішнього кута, розмір якого перевищує 180°. Опуклі багатокутники можуть мати три і більше сторін. У опуклому многокутнику всі діагоналі лежать всередині замкнутої фігури. Типовими прикладами опуклих багатокутників є трикутники, усі опуклі чотирикутники, а також правильні п’ятикутники та шестикутники.
Увігнутий многокутник
Увігнутий багатокутник має принаймні один внутрішній кут, який є рефлексним кутом і спрямований всередину. Увігнуті багатокутники мають мінімум чотири сторони. Цей тип багатокутника має принаймні один внутрішній кут розміром понад 180°. У увігнутих многокутниках деякі діагоналі виходять за межі фігури. Приклади увігнутих багатокутників включають дротик або наконечник стріли в чотирикутниках, а також певні неправильні п’ятикутники та шестикутники.
Різниця між увігнутими та опуклими багатокутниками
Давайте подивимося різницю між опуклим і увігнутим багатокутником у таблиці нижче:

| Опуклий многокутник | Увігнутий многокутник |
|---|---|
| Весь периметр опуклої форми виходить назовні без будь-яких внутрішніх поглиблень. | Увігнута форма має принаймні одну частину, спрямовану всередину, що вказує на наявність вм’ятини. |
| У опуклому многокутнику всі внутрішні кути менші за 180°. | У увігнутому многокутнику існує принаймні один внутрішній кут, що перевищує 180°. |
| Будь-яка лінія, що з’єднує дві вершини опуклої фігури, повністю лежить у межах фігури. | Лінія, що з’єднує будь-які дві вершини увігнутої форми, може перетинати або не перетинати внутрішню частину фігури. |
Багатокутники на основі меж
Багатокутники можна класифікувати на основі характеру їхніх меж на два основні типи:
- Простий багатокутник
- Складний многокутник
Простий багатокутник
Простий багатокутник характеризується сингулярною межею, яка не перетинається. Іншими словами, він не перетинає сам себе, і складається з однієї межі.
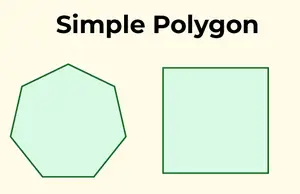
Прості багатокутники
Складний многокутник
З іншого боку, складний багатокутник визначається самим перетином. Він складається з кількох меж у своїй структурі. У складних багатокутниках межі перетинаються, утворюючи кілька окремих областей усередині багатокутника.

Складний многокутник
Докладніше про Типи багатокутників.
Формули багатокутників
Є кілька формул, пов'язаних з многокутниками в геометрії. Деякі з найбільш часто використовуваних включають:
- Формула площі
- Формула периметра
- Кількість діагоналей
Усі формули, пов’язані з різними багатокутниками, обговорюються нижче:
Площа многокутників
Площа багатокутника представляє загальний простір, який він займає в двовимірній площині, визначається за допомогою спеціальних формул на основі кількості сторін і класифікації багатокутника. Формули площі такі:
| Площа багатокутника | Формула |
|---|---|
| Площа трикутника | 1/2 × основа × висота |
| Площа паралелограма | База × Висота |
| Площа прямокутника | Довжина × Ширина |
| Площа площі | (Сбоку)2 |
| 1/2 × діагональ1× діагональ2 | |
| Площа трапеції поліморфізм java | 1/2 × висота × сума паралельних сторін |
| (5/2) × довжина сторони × апофема | |
| Площа шестикутника | {(3√3)/2} сторона2 |
| Площа семикутника | 3,643 × Сторона2 |
Периметр многокутників
Периметр двовимірної форми представляє загальну довжину її зовнішньої межі. Для багатокутників периметр обчислюється таким чином:
| Периметр многокутника | Формула |
|---|---|
| Периметр трикутника | Сума трьох сторін |
| Периметр паралелограма | 2 (сума суміжних сторін) |
| Периметр прямокутника | 2 (довжина + ширина) |
| Периметр квадрата | 4 × Сторона |
| Периметр ромба | 4 × Сторона |
| Периметр трапеції | Сума паралельних сторін + сума непаралельних сторін |
| Периметр Пентагону | 5 × Сторона |
| Периметр шестикутника | 6 × Сторона |
| Периметр семикутника | 7 × Сторона |
Формула діагоналі многокутника
Діагональ багатокутника — це відрізок, утворений з’єднанням двох несуміжних вершин.
Кількість діагоналей у багатокутнику = n(n−3)/2,
Де «n» означає кількість сторін багатокутника.
Докладніше про Формула діагоналі многокутника .
Кути в многокутниках
У геометрії кути в багатокутниках відносяться до кутів, утворених сторонами багатокутника, як всередині, так і зовні багатокутника. Таким чином, у многокутнику можуть бути обидва кути, тобто
- Внутрішні кути
- Зовнішні кути
Давайте докладніше обговоримо формулу для цих кутів:
Формула внутрішнього кута многокутників
Внутрішніми кутами багатокутника є кути, утворені між його суміжними сторонами, і рівні у випадку правильного многокутника. Кількість внутрішніх кутів відповідає кількості сторін багатокутника.
Сума внутрішніх кутів «S» у багатокутнику з «n» сторін обчислюється як
S = (n – 2) × 180°
Де «n» означає кількість сторін.
Формула зовнішнього кута многокутників
Кожен зовнішній кут правильного многокутника утворюється продовженням однієї з його сторін (за або проти годинникової стрілки) і вимірюванням кута між цим розширенням і прилеглою стороною. У правильному многокутнику всі зовнішні кути рівні
Загальна сума зовнішніх кутів будь-якого багатокутника дорівнює 360°
тому
Кожен зовнішній кут задано 360°/n
Де «n» — кількість сторін.
Сума внутрішніх і відповідних зовнішніх кутів у будь-якій вершині багатокутника завжди дорівнює 180 градусам, виражаючи додаткове співвідношення:
Внутрішній кут + зовнішній кут = 180°
Зовнішній кут = 180° – внутрішній кут
Висновок
- Багатокутник — замкнута фігура, обмежена трьома або більше відрізками
- Сума внутрішніх кутів: Сума всіх внутрішніх кутів n-стороннього многокутника визначається формулою (n–2)×180°.
- Кількість діагоналей: Для багатокутника з n сторонами кількість діагоналей обчислюється за формулою n(n–3)/2.
- Трикутники, утворені діагоналями: Кількість трикутників, утворених з’єднанням діагоналей з одного кута багатокутника, дорівнює n–2.
- Внутрішній кут правильного многокутника: Міра кожного внутрішнього кута в n-сторонньому правильному многокутнику дорівнює {(n–2)×180°}/n.
- Зовнішній кут правильного многокутника: Міра кожного зовнішнього кута в n-сторонньому правильному многокутнику дорівнює 360°/n.
Також читайте
- Майдан
- Паралелограм
- Прямокутник
Розв’язані приклади на багатокутник з математики
Приклад 1: Розглянемо чотирикутник із чотирма сторонами. Знайдіть суму всіх його внутрішніх кутів чотирикутника.
рішення:
Формула суми внутрішніх кутів n-стороннього правильного многокутника = (n − 2) × 180°
Сума всіх внутрішніх кутів чотирикутника = (4 – 2) × 180°
Сума всіх внутрішніх кутів чотирикутника = 2 × 180°
Сума всіх внутрішніх кутів чотирикутника дорівнює 360°
Отже, сума всіх внутрішніх кутів чотирикутника дорівнює 360°.
Приклад 2. Розглянемо правильний багатокутник із заданим співвідношенням зовнішнього та внутрішнього кутів 7:3. Визначте вид многокутника.
рішення:
Співвідношення зовнішнього та внутрішнього кутів 7:3.
Припустимо, що зовнішній і внутрішній кути багатокутника дорівнюють 7x і 3x.
Сума зовнішніх і внутрішніх кутів будь-якого многокутника дорівнює 180°.
7x + 3x = 180°
10x = 180°
х = 18°
Зовнішній кут = 18°
Кількість сторін = 360°/зовнішній кут
= 360°/18°
= 20
Отже, даний многокутник є ікосагоником, оскільки має 20 сторін.
Приклад 3: кожен зовнішній кут багатокутника дорівнює 90 градусам. Визначте тип багатокутника?
рішення:
Відповідно до формули, кожен зовнішній кут = 360°/n
Тут n=кількість сторін.
90°= 360°/n
n = 360°/90°= 4
Отже, розглянутий многокутник є чотирикутником, оскільки він має чотири сторони.
Приклад 4: Сторони дорівнюють 10 м, 10 м, 8 м, 8 м, 5 м, 5 м, 9 м, 9 м. Скільки метрів мотузки знадобиться для периметра?
рішення:
Щоб знайти довжину мотузки, необхідної для периметра, потрібно підсумувати довжини всіх сторін:
Периметр = 10 м + 10 м + 8 м + 8 м + 5 м + 5 м + 9 м + 9 м
Периметр = 64 м.
Отже, загалом на Периметр знадобиться 64 метри мотузки.
Практичні запитання про багатокутники в геометрії
Нижче наведено кілька практичних запитань на основі формули багатокутників:
Q1. Якщо один кут п’ятикутника дорівнює 140°, визначте величину найбільшого кута, якщо решта кутів відносяться як 1:2:3:4.
Q2. Знайдіть кількість сторін багатокутника, якщо сума внутрішніх кутів багатокутника дорівнює 160°.
Q3. Число сторін у двох правильних многокутниках відношиться як 2:3, а відношення їхніх внутрішніх кутів — 4:5. Знайдіть відповідні числа сторін цих многокутників.
Q4. Визначте загальну суму кутів семикутника.
Q5. Обчисліть суму зовнішніх кутів п’ятикутника.
Q6. Скільки сторін має шестикутник?
- 4
- 6
- 8
- 10
Q7. Що з наведеного не є правильним многокутником?
jsp javatpoint
- Трикутник
- Майдан
- П'ятикутник
- Паралелограм
Поширені запитання про багатокутники в математиці
Що таке многокутник в математиці?
У математиці багатокутник відноситься до замкнутої двовимірної фігури, утвореної з’єднанням трьох або більше прямих ліній. Термін «багатокутник» походить з грецької мови, де багатокутник означає багато, а кут — кут.
Який найменший багатокутник?
Найменший утворений багатокутник — трикутник із трьома сторонами.
Що таке 20-кутник?
20-кутник — двадцятикутник у геометрії.
Чому дорівнює загальна сума зовнішніх кутів многокутника?
Сума зовнішніх кутів многокутника дорівнює 360°.
Чи можна коло класифікувати як багатокутник?
Багатокутник — замкнута фігура, що складається з прямолінійних сегментів. Коло – замкнута фігура, але вона складається з кривої. Отже, коло не є многокутником.
Що таке сума внутрішніх кутів многокутника?
Сума внутрішніх кутів багатокутника визначається як (n–2)×180°, де n – кількість сторін багатокутника.
