А Min-Heap визначається як вид Структура даних купи — це тип двійкового дерева, який зазвичай використовується в інформатиці для різних цілей, включаючи сортування, пошук і впорядкування даних.
Введення в Min-Heap – Навчальні посібники зі структури даних і алгоритмів
Призначення та випадки використання Min-Heap:
- Реалізація пріоритетної черги: Одним із основних застосувань структури даних купи є реалізація пріоритетних черг.
- Алгоритм Дейкстри : Алгоритм Дейкстри — це алгоритм найкоротшого шляху, який знаходить найкоротший шлях між двома вузлами на графі. Мінімальна купа може бути використана для відстеження невідвіданих вузлів із найменшою відстанню від вихідного вузла.
- Сортування: Мінімальна купа може бути використана як алгоритм сортування для ефективного сортування колекції елементів у порядку зростання.
- Середній результат: Min heap можна використовувати для ефективного знаходження медіани потоку чисел. Ми можемо використовувати одну мінімальну купу для зберігання більшої половини чисел і одну максимальну купу для зберігання меншої половини. Медіана буде коренем мінімальної купи.
Структура даних Min-Heap на різних мовах:
1. Min-Heap в C++
Мінімальна купа може бути реалізована за допомогою priority_queue контейнер зі стандартної бібліотеки шаблонів (STL). The priority_queue контейнер — це тип адаптера контейнера, який забезпечує спосіб зберігання елементів у структурі даних, подібній до черги, у якій кожен елемент має пов’язаний з ним пріоритет.
Синтаксис :
C++ priority_queue < int, vector , більше > minH;>
2. Min-Heap в Java
У Java мінімальну купу можна реалізувати за допомогою PriorityQueue клас від пакет java.util . Клас PriorityQueue — це пріоритетна черга, яка забезпечує спосіб зберігання елементів у структурі даних, подібній до черги, у якій кожен елемент має пов’язаний з ним пріоритет.
Синтаксис :
Java PriorityQueue minHeap = новий PriorityQueue ();>
3. Min-Heap в Python
У Python мінімальну купу можна реалізувати за допомогою heapq модуль, який надає функції для реалізації куп. Зокрема, heapq Модуль забезпечує спосіб створення та керування структурами даних купи.
діаграма моделі e-r
Синтаксис:
Python heap = [] heapify(heap)>
4. Min-Heap в C#
У C# мінімальну купу можна реалізувати за допомогою класу PriorityQueue з System.Collections.Generic простір імен . Клас PriorityQueue — це пріоритетна черга, яка забезпечує спосіб зберігання елементів у структурі даних, подібній до черги, у якій кожен елемент має пов’язаний з ним пріоритет.
Синтаксис:
C# var minHeap = new PriorityQueue ();>
5. Min-heap в JavaScript
Мінімальна купа — це бінарне дерево, де кожен вузол має значення, менше або дорівнює дочірнім вузлам. У JavaScript ви можете реалізувати мінімальну купу за допомогою масиву, де перший елемент представляє кореневий вузол, а дочірні елементи вузла за індексом i розташовані за індексами 2і+1 і 2і+2.
Синтаксис:
JavaScript const minHeap = new MinHeap();>
Різниця між мінімальною та максимальною купою:
|
| Мінімальна купа | Макс Хіп |
|---|---|---|
| 1. | У Min-Heap ключ, присутній у кореневому вузлі, має бути меншим або дорівнювати ключам, присутнім у всіх його дочірніх вузлах. | У Max-Heap ключ, присутній у кореневому вузлі, повинен бути більшим або дорівнювати ключам, присутнім у всіх його дочірніх вузлах. |
| 2. | У Min-Heap мінімальний ключовий елемент присутній у корені. | У Max-Heap максимальний ключовий елемент присутній у корені. |
| 3. | Min-Heap використовує зростаючий пріоритет. | Max-Heap використовує низхідний пріоритет. |
| 4. | При побудові Min-Heap найменший елемент має пріоритет. | При побудові Max-Heap найбільший елемент має пріоритет. |
| 5. | У Min-Heap найменший елемент є першим, який виривається з купи. | У Max-Heap найбільший елемент є першим, який виривається з купи. |
Внутрішня реалізація структури даних Min-Heap:
А Мінімальна купа зазвичай представляється у вигляді масиву .
- Кореневий елемент буде at Прибуток[0] .
- Для будь-якого i-го вузла Arr[i] :
- Arr[(i -1) / 2] повертає свій батьківський вузол.
- Arr[(2 * i) + 1] повертає свій лівий дочірній вузол.
- Arr[(2 * i) + 2] повертає правий дочірній вузол.
Внутрішнє впровадження Min-Heap вимагає 3 основних кроків:
- Вставка : Щоб вставити елемент у мінімальну купу, ми спочатку додаємо елемент до кінця масиву, а потім регулюємо властивість купи, постійно міняючи елемент його батьківським елементом, доки він не займе правильну позицію.
- Видалення : Щоб видалити мінімальний елемент із мінімальної купи, ми спочатку міняємо кореневий вузол останнім елементом у масиві, видаляємо останній елемент, а потім регулюємо властивість купи, постійно міняючи місцями елемент найменшим дочірнім елементом, доки він не опиниться в правильне положення.
- Heapify : операцію heapify можна використовувати для створення мінімальної купи з несортованого масиву.
Операції над структурою даних Min-heap та їх реалізація:
Ось кілька поширених операцій, які можна виконати над структурою даних купи,
1. Вставка в структуру даних Min-Heap :
Елементи можна вставляти в купу за подібним підходом, як описано вище для видалення. Ідея полягає в тому, щоб:
- Операція вставки в міні-купу включає наступні кроки:
- Додайте новий елемент у кінець купи, у наступну доступну позицію на останньому рівні дерева.
- Порівняйте новий елемент з його батьківським. Якщо батьківський елемент більший за новий елемент, поміняйте їх місцями.
- Повторюйте крок 2, доки батьківський елемент не стане меншим або дорівнює новому елементу або доки новий елемент не досягне кореня дерева.
- Тепер новий елемент займає правильну позицію в мінімальній купі, і властивість купи виконано.
Ілюстрація:
Припустимо, що купа є мінімальною купою, як:
Вставка в Min-Heap
Реалізація операції вставки в Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Додати новий елемент у кінець купи heap.push_back(value); // Отримання індексу останнього елемента int index = heap.size() - 1; // Порівняйте новий елемент із його батьківським // місцем, якщо необхідно, while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Перейти вгору по дереву до батьківського // елемента index = (index - 1) / 2; } } // Головна функція для перевірки функції insert_min_heap int main() { вектор купа; int values[] = { 10, 7, 11, 5, 4, 13 }; int n = sizeof(значення) / sizeof(значення[0]); для (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && heap[(index - 1) / 2]> heap[index]) { swap(heap, index, (index - 1) / 2); // Перейти вгору по дереву до батьківського // елемента index = (index - 1) / 2; } } // Функція для обміну місцями двох елементів у масиві public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = темп; } // Основна функція для перевірки функції insertMinHeap public static void main(String[] args) { int[] heap = new int[6]; int[] значення = { 10, 7, 11, 5, 4, 13 }; int size = 0; для (int i = 0; i< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 і купа[(індекс - 1) // 2]> купа[індекс]: купа[індекс], купа[(індекс - 1) // 2] = купа[(індекс - 1) // 2], купа[ index] # Переміщення вверх по дереву до батьківського елемента поточного елемента index = (index - 1) // 2 купа = [] values = [10, 7, 11, 5, 4, 13] для значення у values: insert_min_heap( купа, значення) print(f'Вставлено {value} у min-heap: {heap}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List heap, int value) { // Додати новий елемент у кінець купи heap.Add(value); // Отримання індексу останнього елемента int index = heap.Count - 1; // Порівняйте новий елемент із його батьківським і // за необхідності поміняйте місцями while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index]; купа[індекс] = купа[(індекс - 1) / 2]; купа[(індекс - 1) / 2] = temp; // Перейти вгору по дереву до батьківського // елемента index = (index - 1) / 2; } } // Основна функція для перевірки функції InsertMinHeap public static void Main() { List купа = новий список (); int[] значення = { 10, 7, 11, 5, 4, 13 }; foreach(int value in values) { InsertMinHeap(heap, value); Console.Write('Inserted ' + value + ' into the min-heap: '); foreach(int елемент у купі) { Console.Write(element + ' '); } Console.WriteLine(); } } }> Javascript function insertMinHeap(heap, value) { heap.push(value); let index = heap.length - 1; let parentIndex = Math.floor((index - 1) / 2); while (index>0 && heap[parentIndex]> heap[index]) { [heap[index], heap[parentIndex]] = [heap[parentIndex], heap[index]]; індекс = parentIndex; parentIndex = Math.floor((індекс - 1) / 2); } } // Приклад використання const heap = []; значення const = [10, 7, 11, 5, 4, 13]; for (const значення значень) { insertMinHeap(heap, value); console.log(`Вставлено ${value} у міні-кучу: ${heap}`); }> Вихід
Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Часова складність: O(log(n)) ( де n – кількість елементів у купі )
Допоміжний простір: O(n)
2. Видалення в структурі даних Min-Heap :
Видалення найменшого елемента (кореневого) з min heap. Корінь замінюється останнім елементом у купі, а потім властивість купи відновлюється шляхом заміни нового кореня його найменшим дочірнім елементом, доки батьківський елемент не стане меншим за обох дочірніх елементів або доки новий корінь не досягне листкового вузла.
- Замініть корінь або елемент, який потрібно видалити, на останній елемент.
- Видалити останній елемент із купи.
- Оскільки останній елемент тепер розміщено на позиції кореневого вузла. Отже, він може не відповідати властивості heap. Тому нагромаджуйте останній вузол, розміщений на місці кореня.
Ілюстрація :
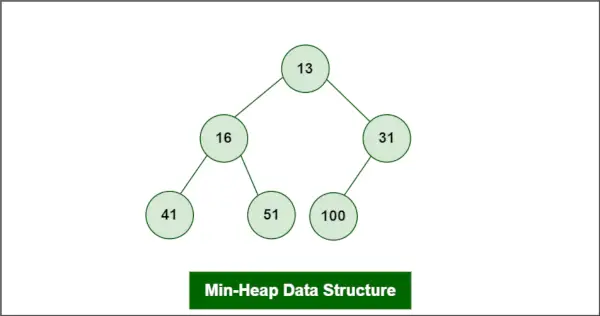
Припустимо, що купа є мінімальною купою, як:
Структура даних Min-Heap
Елемент, який потрібно видалити, це root, тобто 13.
латексні розміри текступроцес :
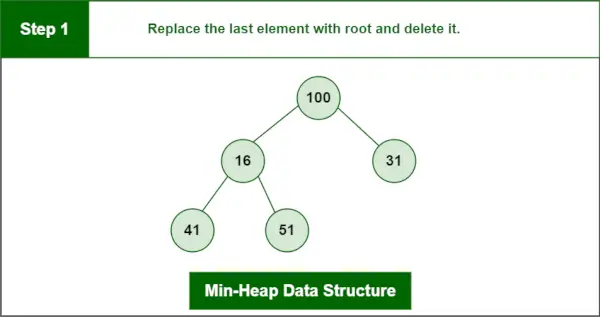
Останній елемент 100.
Крок 1: Замініть останній елемент на root і видаліть його.
Структура даних Min-Heap
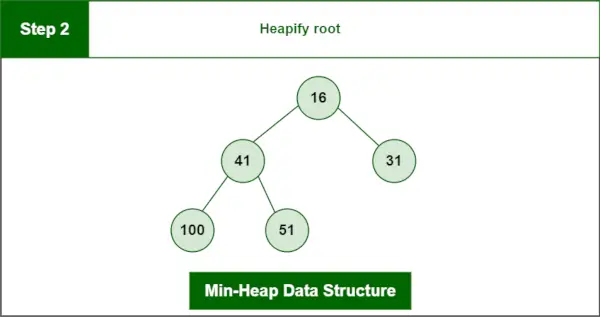
Крок 2 : Heapify корінь.
Остаточна купа:
Структура даних Min-Heap
Реалізація операції видалення в Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Додати новий елемент у кінець купи heap.push_back(value); // Отримання індексу останнього елемента int index = heap.size() - 1; // Порівняйте новий елемент із його батьківським // місцем, якщо необхідно, while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Перейти вгору по дереву до батьківського // елемента index = (index - 1) / 2; } } // Функція видалення вузла з мінімальної купи void delete_min_heap(вектор & heap, int value) { // Знайти індекс елемента, який потрібно видалити int index = -1; для (int i = 0; i< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector купа; int values[] = { 13, 16, 31, 41, 51, 100 }; int n = sizeof(значення) / sizeof(значення[0]); для (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List heap, int value) { // Додати новий елемент у кінець купи heap.add(value); // Отримання індексу останнього елемента int index = heap.size() - 1; // Порівняйте новий елемент із його батьківським і // за необхідності замініть місцями while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (індекс - 1) / 2); // Перейти вгору по дереву до батьківського // елемента index = (index - 1) / 2; } } // Функція для видалення вузла з мінімальної купи public static void deleteMinHeap(List heap, int value) { // Знайти індекс елемента, який потрібно видалити int index = -1; для (int i = 0; i< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List heap = новий ArrayList (); int[] значення = { 13, 16, 31, 41, 51, 100 }; int n = values.length; для (int i = 0; i< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 і купа[(індекс - 1) // 2]> купа[індекс]: купа[індекс], купа[(індекс - 1) // 2] = купа[(індекс - 1) // 2], купа[ index] index = (index - 1) // 2 def delete_min_heap(heap, value): index = -1 for i in range(len(heap)): if heap[i] == value: index = i break if index == -1: повернути heap[index] = heap[-1] heap.pop() while True: left_child = 2 * index + 1 right_child = 2 * index + 2 smallest = index if left_child< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List купа = новий список (); public void Insert(int value) { heap.Add(value); int index = heap.Count - 1; while (index> 0 && heap[(index - 1) / 2]> heap[index]) { Swap(index, (index - 1) / 2); індекс = (індекс - 1) / 2; } } public void Delete(int value) { int index = heap.IndexOf(value); if (index == -1) { return; } heap[index] = heap[heap.Count - 1]; heap.RemoveAt(heap.Count - 1); while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * індекс + 2; int найменший = індекс; якщо (ліворучДитина< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> Javascript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && купа[flr]> купа[індекс]; flr = Math.floor((index - 1) / 2)) { [heap[index], heap[flr]] = [ heap[flr], heap[index], ]; // Переміщення вверх по дереву до батьківського елемента поточного елемента index = Math.floor((index - 1) / 2); } } function deleteMinHeap(heap, value) { // Знайдіть індекс елемента, який потрібно видалити let index = -1; для (нехай i = 0; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));> Вихід
Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
Часова складність : O(log n), де n – кількість елементів у купі
Допоміжний простір: O(n)
3. Операція Peek на структурі даних Min-Heap:
Щоб отримати доступ до мінімального елемента (тобто кореня купи), повертається значення кореневого вузла. Часова складність перегляду в міні-купі становить O(1).
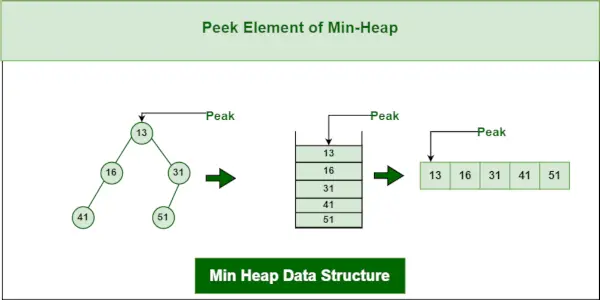
Мінімальна структура даних купи
Реалізація операції Peek у Min-Heap:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , більше > minHeap; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Отримання пікового елемента (тобто найбільшого елемента) int peakElement = minHeap.top(); // Надрукувати піковий елемент cout<< 'Peak element: ' << peakElement << std::endl; return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = новий PriorityQueue(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Отримання пікового елемента (тобто найбільшого елемента) int peakElement = minHeap.peek(); // Надрукувати піковий елемент System.out.println('Піковий елемент: ' + peakElement); } }> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Отримання пікового елемента (тобто найменшого елемента) int peakElement = minHeap.Peek(); // Надрукувати піковий елемент Console.WriteLine('Піковий елемент: ' + peakElement); } }> Javascript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>а - б); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Отримання пікового елемента (тобто найменшого елемента) const peakElement = minHeap.peek(); // Надрукувати піковий елемент console.log(`Піковий елемент: ${peakElement}`);> Вихід
Peak element: 1>
Часова складність : У мінімальній купі, реалізованій за допомогою масиву або списку, піковий елемент може бути доступний у постійний час, O(1), оскільки він завжди розташований у корені купи.
У міні-купі, реалізованій за допомогою бінарного дерева, піковий елемент також може бути доступний за час O(1), оскільки він завжди розташований у корені дерева.
Допоміжний простір: O(n)
4. Операція Heapify над структурою даних Min-Heap:
Операцію heapify можна використовувати для створення мінімальної купи з несортованого масиву. Це робиться, починаючи з останнього вузла, що не є листом, і багаторазово виконуючи операцію «спускання», поки всі вузли не задовольнять властивість купи.
Операція Heapify у Min Heap
Реалізація операції Heapify в Min-Heap:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int найменший = i; int l = 2*i + 1; int r = 2*i + 2; якщо (л< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector arr = {10, 5, 15, 2, 20, 30}; cout<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); cout<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // Припустимо, що корінь є найменшим елементом спочатку int smallest = i; // Обчислення індексів лівого та правого дочірніх елементів поточного вузла int l = 2 * i + 1; int r = 2 * i + 2; // Порівнюємо ліву дочірню частину з поточною найменшою if (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Оригінальний масив: '); // Вивести вихідний масив для (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
Мінальна купа після операції heapify: '); // Надрукувати мінімальну купу після операції heapify для (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Python def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int i, int n) { int smallest = i; int left = 2 * i + 1; int right = 2 * i + 2; // Порівнюємо лівий дочірній елемент із поточним найменшим вузлом. якщо (ліворуч< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = новий список { 10, 5, 15, 2, 20, 30 }; Console.Write('Оригінальний масив: '); foreach (int num in arr) Console.Write(num + ' '); // Виконати операцію heapify на міні-купі. for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap після операції heapify: '); foreach (int num in arr) Console.Write(num + ' '); } }> Javascript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.length); // Надрукувати мінімальну купу після операції heapify console.log('Min-Heap після операції heapify: ' + arr.join(' ')); } // Виклик функції main для запуску процесу main();> Вихід
Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>
Часова складність heapify у min-heap становить O(n).
5. Операція пошуку в структурі даних Min-Heap:
Щоб знайти елемент у мінімальній купі, можна виконати лінійний пошук по масиву, який представляє купу. Однак часова складність лінійного пошуку становить O(n), що не є ефективним. Тому пошук не є широко використовуваною операцією в мінімальній купі.
Ось приклад коду, який показує, як шукати елемент у мінімальній купі за допомогою std::find() :
C++ #include using namespace std; int main() { priority_queue , більше > min_heap; // приклад максимальної купи min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); int element = 6; // елемент для пошуку bool found = false; // Скопіюйте мінімальну купу до тимчасової черги та знайдіть // елемент std::priority_queue , більше > temp = min_heap; while (!temp.empty()) { if (temp.top() == element) { found = true; перерва; } temp.pop(); } якщо (знайдено) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = новий PriorityQueue(); min_heap.add( 3); // вставити елементи в пріоритетну чергу min_heap.offer(1); min_heap.offer(4); min_heap.offer(1); min_heap.offer(6); int element = 6; // елемент для пошуку boolean found = false; // Скопіюйте мініатюрну купу до тимчасової черги та знайдіть // елемент PriorityQueue temp = new PriorityQueue(min_heap); while (!temp.isEmpty()) { if (temp.poll() == element) { found = true; перерва; } } if (знайдено) { System.out.println( 'Елемент знайдено в мінімальній купі.'); } else { System.out.println( 'Елемент не знайдено в мінімальній купі.'); } } }> Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // приклад min heap minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); int element = 6; // елемент для пошуку bool found = false; // Скопіюйте мініатюрну купу до тимчасової черги та знайдіть // елемент var temp = new PriorityQueue (minHeap); while (temp.Count> 0) { if (temp.Peek() == element) { found = true; перерва; } temp.Dequeue(); } if (знайдено) { Console.WriteLine( 'Елемент знайдено в мінімальній купі.'); } else { Console.WriteLine( 'Елемент не знайдено в мінімальній купі.'); } } }> Javascript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { якщо (temp.peek() == елемент) { знайдено = істина; перерва; } temp.dequeue(); } if (знайдено) { console.log('Елемент знайдено в мінімальній купі.'); } else { console.log('Елемент не знайдено в мінімальній купі.'); }> Вихід
Element found in the min heap.>
Аналіз складності :
The часова складність цієї програми O(n log n) , де п кількість елементів у пріоритетній черзі.
Операція вставки має часову складність O(log n) у гіршому випадку, оскільки потрібно підтримувати властивість купи. Операція пошуку передбачає копіювання пріоритетної черги до тимчасової черги, а потім проходження тимчасової черги, що займає O(n log n) час у гіршому випадку, оскільки кожен елемент потрібно скопіювати та вилучити з черги, а пріоритетну чергу потрібно перебудувати для кожної операції.
The складність простору програми є O(n) тому що зберігає п елементів у пріоритетній черзі та створює тимчасову чергу з п елементів.
Застосування структури даних Min-Heap:
- Сортування купи: Мінімальна купа використовується як ключовий компонент алгоритму сортування купи, який є ефективним алгоритмом сортування з часовою складністю O(nlogn).
- Пріоритетна черга: Пріоритетну чергу можна реалізувати за допомогою мінімальної структури даних купи, де елемент із мінімальним значенням завжди знаходиться в корені.
- Алгоритм Дейкстри: В алгоритмі Дейкстри мінімальна купа використовується для зберігання вершин графа на мінімальній відстані від початкової вершини. Вершина з мінімальною відстанню завжди знаходиться в корені купи.
- Кодування Хаффмана: У кодуванні Хаффмана мінімальна купа використовується для реалізації черги пріоритетів для створення оптимального префіксного коду для заданого набору символів.
- Об’єднати K відсортованих масивів: Маючи K відсортованих масивів, ми можемо ефективно об’єднати їх в один відсортований масив, використовуючи мінімальну структуру даних купи.
Переваги Min-heap Data Structure:
- Ефективне вставлення та видалення : Мінімальна купа дозволяє швидко вставляти та видаляти елементи з часовою складністю O(log n), де n — кількість елементів у купі.
- Ефективне отримання мінімального елемента: Мінімальний елемент у мінімальній купі завжди знаходиться в корені купи, який можна отримати за час O(1).
- Економія простору: Мінімальна купа — це компактна структура даних, яка може бути реалізована за допомогою масиву або бінарного дерева, що робить її ефективним у просторі.
- Сортування: Мінімальна купа може бути використана для реалізації ефективного алгоритму сортування, такого як сортування купи з часовою складністю O(n log n).
- Пріоритетна черга: Мінімальна купа може бути використана для реалізації черги пріоритетів, де елемент із мінімальним пріоритетом може бути ефективно отриманий за час O(1).
- Універсальність: Мінімальна купа має кілька застосувань в інформатиці, включаючи алгоритми графів, стиснення даних і системи баз даних.
Загалом мінімальна купа — це корисна та універсальна структура даних, яка пропонує ефективні операції, ефективність простору та має кілька застосувань у інформатиці.