Трикутники — тригранні замкнені багатокутники, утворені перетином трьох прямих. У повсякденному житті це зустрічається дуже часто. Це одна з основних форм геометрії. Він має три сторони, три кути і три вершини. Прямокутний трикутник — це такий, у якого один із кутів завжди дорівнює 90°. Теорема Піфагора отримано для прямокутних трикутників, яке стверджує, що квадрат гіпотенузи (найдовшої сторони) дорівнює сумі квадратів основи та перпендикуляра.

За довжиною принаймні двох сторін прямокутного трикутника можна знайти значення будь-якого кута прямокутного трикутника. Для цього ми використовуємо різні тригонометричні функції, такі як синус, косинус, тангенс, котангенс, сек і косек. Вони допомагають нам зв’язати кути прямокутного трикутника з його сторонами.

Властивості

• Серед трьох вершин є вершина прямого кута
• Сторона, протилежна вершині прямокутника, називається гіпотенуза .
• Довжина сторін відповідає теоремі Піфагора, яка стверджує

гіпотенуза ² = база ² + висота ²

• Гіпотенуза — найдовша сторона прямокутного трикутника.
• Кути, крім прямого, є гострими, оскільки значення менше 90^О

Тригонометричні функції

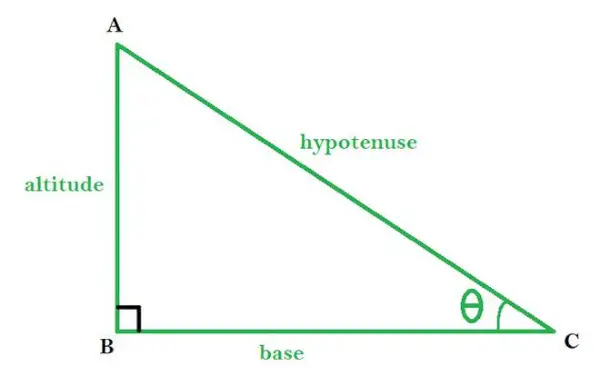
ABC — прямокутний трикутник із ∠B як прямий кут

непорядковий обхід бінарного дерева

• cosθ: Це дає відношення основи до гіпотенузи прямокутного трикутника.

cosθ = основа / гіпотенуза

• sinθ: Це дає відношення висоти до гіпотенузи прямокутного трикутника.

sinθ = висота / гіпотенуза

• tanθ: Це відношення висоти до основи прямокутного трикутника.

tanθ = висота / база

• cotθ: Це обернене tanθ
• secθ: Це обернене cosθ
• cosecθ: Це обернене sinθ

Щоб знайти кути прямокутного трикутника, можна взяти тригонометричну величину, обернену відношенню заданих сторін трикутника.

приклад:

Якщо sinθ = x, то ми можемо написати

θ = sin ^-1 х.

Це повертає кут, для якого значення синуса кута дорівнює x.

Подібним чином існує cos^-1θ, отже^-1я, ліжечко^-1θ, сек^-1θ і cosec^-1i

Зразки завдань

Запитання 1. Дано прямокутний трикутник, основа якого дорівнює 10 см, а гіпотенуза дорівнює 20 см. Знайдіть значення кута при основі.

рішення:

Дано, основа = 10 см

Гіпотенуза = 20 см

Нехай значення кута основи дорівнює θ. Ми можемо писати

cosθ = основа / гіпотенуза = 10/20 = 1/2

θ = cos^-1(1/2) = 60^О

Отже, величина кута при основі дорівнює 60 ^О .

Запитання 2. Знайдіть значення кутів прямокутного трикутника, якщо один із гострих кутів удвічі більший за інший.

рішення:

Оскільки ми знаємо, що сума всіх трьох кутів у трикутнику дорівнює 180^О.

Оскільки один із кутів дорівнює 90^Оа один із гострих кутів удвічі більший за інший, ми можемо розглядати їх як θ і 2θ.

Отже, ми можемо писати

90^О+ θ + 2θ = 180^О

3θ = 180^О– 90^О

3θ = 90^О

θ = 90^О/3 = 30 ^О

2θ = 2 × 30^О= 60 ^О

Отже, кути дорівнюють 30 ^О , 60 ^О , і 90 ^О .

Запитання 3. Знайти значення кута підйому драбини довжиною 5 м, враховуючи, що основа драбини знаходиться на відстані 3 м від стіни.

рішення:

Оскільки драбина діє як гіпотенуза прямокутного трикутника, а відстань основи дорівнює 3 м, ми можемо написати

Гіпотенуза = 5м

Основа = 3м

Нехай кут підйому дорівнює θ. Отже, ми можемо писати

cosθ = Основа / Гіпотенуза = 3/5

θ = cos^-1(3/5)

θ = 53^О

Таким чином, значення кута підйому дорівнює 53^О.

Запитання 4. Знайдіть значення гіпотенузи, якщо довжина висоти дорівнює 8 м, а кут при основі дорівнює 30 ^О .

рішення:

Дано кут при основі дорівнює 30^Оі висота дорівнює 8 м, ми можемо застосувати функцію синуса, щоб знайти довжину гіпотенузи.

гріх30 ^О = висота / гіпотенуза

гіпотенуза = висота / sin30^О

Оскільки значення sin30^Одорівнює 1/2, ми можемо записати

гіпотенуза = висота / (1/2) = 2 × висота

Отже, гіпотенуза = 2 × 8 = 16 м

Отже, довжина гіпотенузи дорівнює 16м.