У цій статті ми обговоримо порядковий обхід у структурі даних.
Якщо ми хочемо обійти вузли в порядку зростання, тоді ми використовуємо обхід у порядку. Нижче наведено кроки, необхідні для обходу в порядку:
- Відвідайте всі вузли лівого піддерева
- Відвідайте кореневий вузол
- Відвідайте всі вузли правого піддерева
Лінійні структури даних, такі як стек, масив, черга тощо, мають лише один спосіб обходу даних. Але в ієрархічних структурах даних, таких як дерево, існує кілька способів проходження даних. Тут ми обговоримо інший спосіб обходу структури даних дерева, тобто обхід у порядку.
Існує два підходи, які використовуються для обходу в порядку:
- Обхід у порядку за допомогою рекурсії
- Обхід порядку за допомогою ітераційного методу
Слідує техніка безпорядкового обходу Лівий Корінь Правий політики. Тут Left Root Right означає, що спочатку обходиться ліве піддерево кореневого вузла, потім кореневий вузол, а потім праве піддерево кореневого вузла. Тут сама назва порядку говорить про те, що кореневий вузол знаходиться між лівим і правим піддеревами.
Ми обговоримо обхід у порядку, використовуючи як рекурсивні, так і ітераційні методи. Давайте спочатку почнемо з обходу в порядку за допомогою рекурсії.
Обхід у порядку за допомогою рекурсії
Step 1: Recursively traverse the left subtree Step 2: Now, visit the root Step 3: Traverse the right subtree recursively
Приклад непорядкового обходу
Тепер давайте розглянемо приклад обходу в порядку. На прикладі буде простіше зрозуміти процедуру обходу по порядку.
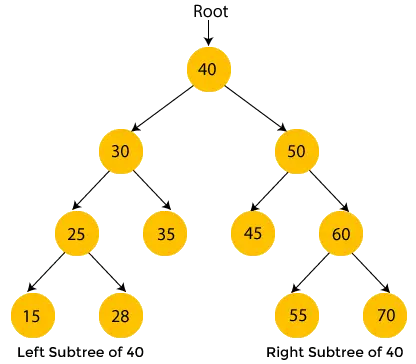
Вузли з жовтим кольором ще не відвідуються. Тепер ми обійдемо вузли наведеного вище дерева за допомогою обходу в порядку.
- Тут 40 є кореневим вузлом. Ми переходимо до лівого піддерева 40, тобто 30, і воно також має піддерево 25, тому ми знову переходимо до лівого піддерева 25, тобто 15. Тут 15 не має піддерева, тому друк 15 і рухатися до свого батьківського вузла, 25.
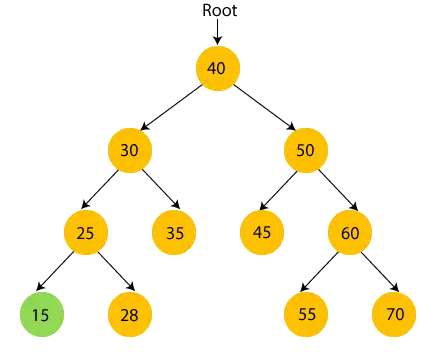
- тепер, надрукувати 25 і перейдіть до правого піддерева 25.
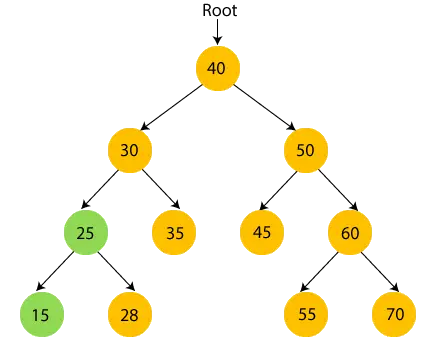
- тепер, друк 28 і перейдіть до кореневого вузла 25, тобто 30.
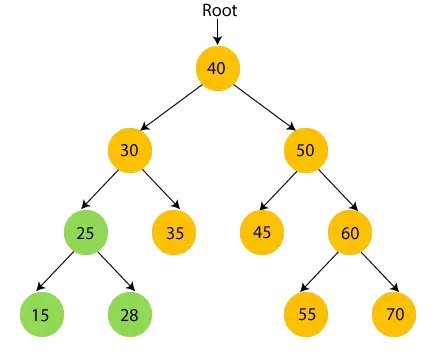
- Отже, відвідано ліве піддерево 30. тепер, надрукувати 30 і перейти до правого дочірнього елемента 30.
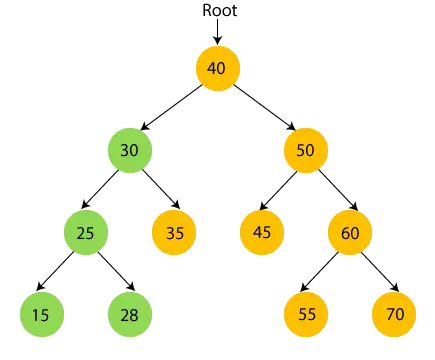
- тепер, надрукувати 35 і перейдіть до кореневого вузла 30.
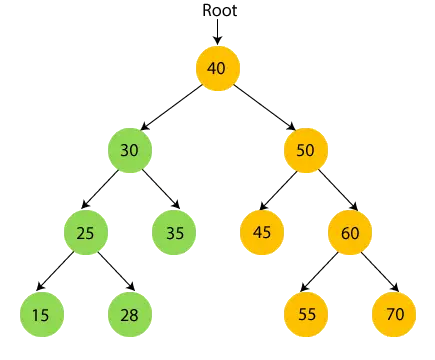
- тепер, надрукувати кореневий вузол 40 і перейти до правого піддерева.
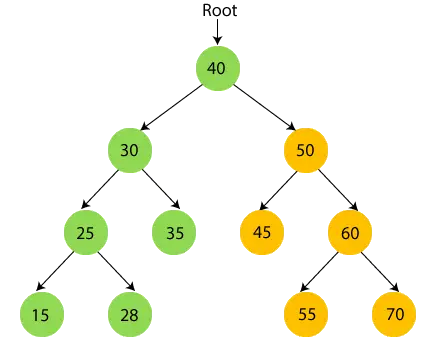
- Тепер рекурсивно пройдіть праве піддерево 40, тобто 50.
50 має піддерево, тому спочатку пройдіть ліве піддерево 50, тобто 45. 45 не має дітей, тому надрукувати 45 і перейдіть до його кореневого вузла.
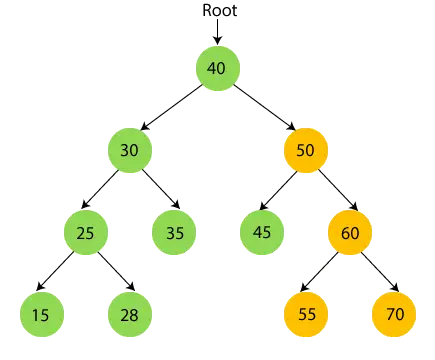
- Зараз надрукувати 50 і перейдіть до правого піддерева 50, тобто 60.
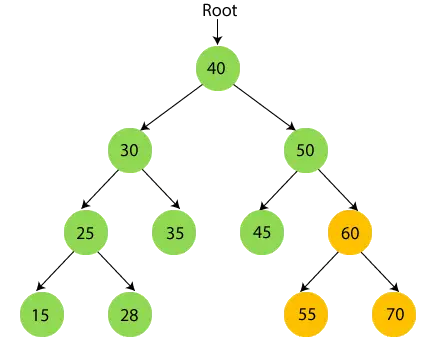
- Тепер рекурсивно перейдіть по правому піддереву 50, тобто 60. 60 має піддерево, тому спочатку пройдіть ліве піддерево 60, тобто 55. 55 не має дітей, тому надрукувати 55 і перейдіть до його кореневого вузла.
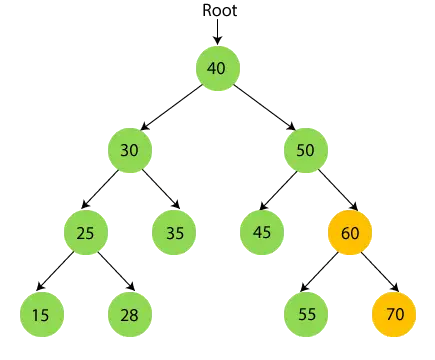
- Зараз надрукувати 60 і перейдіть до правого піддерева 60, тобто 70.
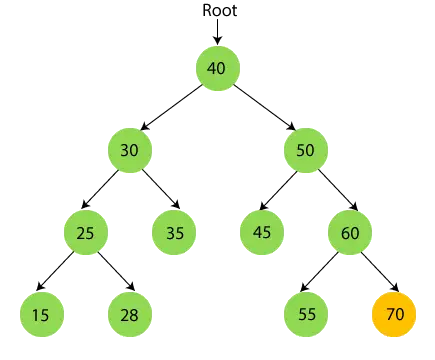
- Зараз надрукувати 70.
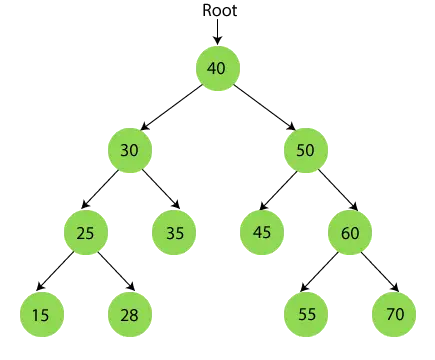
Після завершення обходу за порядком остаточний результат -
{15, 25, 28, 30, 35, 40, 45, 50, 55, 60, 70}
Складність обходу Inorder
Часова складність обходу Inorder становить O(n), де 'n' — розмір бінарного дерева.
У той час як просторова складність обходу в порядку O(1), якщо ми не беремо до уваги розмір стека для викликів функцій. Інакше просторова складність обходу в порядку є O(h), де «h» — висота дерева.
Реалізація Inorder Traversal
Тепер давайте подивимося реалізацію обходу в порядку в різних мовах програмування.
програма: Напишіть програму для реалізації обходу за порядком мовою C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Inorder traversal of given binary tree is -
'); traverseInorder(root); return 0; } Вихід

програма: Напишіть програму для реалізації обходу в порядку в C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); cout<<' '<element<right); } int main() { struct node* root="createNode(39);" root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the inorder traversal of given binary tree is -
'; traverseinorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-14.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(36); bt.root.left = new Node(26); bt.root.right = new Node(46); bt.root.left.left = new Node(21); bt.root.left.right = new Node(31); bt.root.left.left.left = new Node(11); bt.root.left.left.right = new Node(24); bt.root.right.left = new Node(41); bt.root.right.right = new Node(56); bt.root.right.right.left = new Node(51); bt.root.right.right.right = new Node(66); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-15.webp" alt="Inorder Traversal"> <p> <strong>Program:</strong> Write a program to implement inorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/15/inorder-traversal-16.webp" alt="Inorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Вихід

програма: Напишіть програму для реалізації обходу в порядку в Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class InorderTraversal { Node root; InorderTraversal() { root = null; } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + ' '); traverseInorder(node.right); } void traverseInorder() { traverseInorder(root); } public static void main(String args[]) { InorderTraversal pt = new InorderTraversal(); pt.root = new Node(35); pt.root.left = new Node(25); pt.root.right = new Node(45); pt.root.left.left = new Node(20); pt.root.left.right = new Node(30); pt.root.left.left.left = new Node(10); pt.root.left.left.right = new Node(23); pt.root.right.left = new Node(40); pt.root.right.right = new Node(55); pt.root.right.right.left = new Node(50); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println('The Inorder traversal of given binary tree is - '); pt.traverseInorder(); System.out.println(); } } Вихід

Отже, це все про статтю. Сподіваюся, стаття буде для вас корисною та інформативною.











