Спочатку розберемося бінарне дерево і двійкове дерево пошуку окремо, а потім ми розглянемо відмінності між бінарним деревом і бінарним деревом пошуку.
Що таке бінарне дерево?
А Бінарне дерево це
Двійкове дерево можна представити у вигляді:
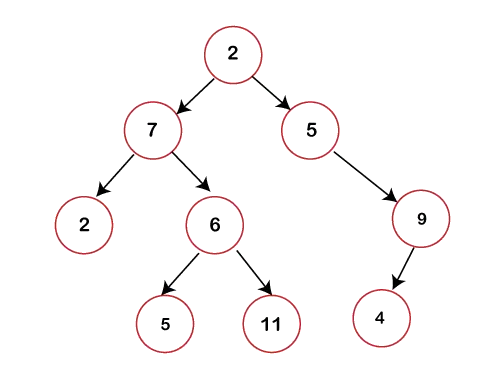
На наведеному вище малюнку ми бачимо, що кожен вузол містить щонайбільше 2 дочірніх вузла. Якщо будь-який вузол не містить лівого чи правого дочірнього елемента, тоді значення вказівника щодо цього дочірнього елемента буде NULL.
Основні терміни, які використовуються в бінарному дереві:
перетворити int на рядок
У бінарному дереві є одне дерево, відоме як a ідеальне бінарне дерево . Це дерево, у якому всі внутрішні вузли повинні містити по два вузли, а всі листові вузли мають бути на однаковій глибині. У випадку ідеального бінарного дерева загальну кількість вузлів у двійковому дереві можна обчислити за допомогою такого рівняння:
n = 2m+1-1
алгоритм rr
де n – кількість вузлів, m – глибина вузла.
Що таке бінарне дерево пошуку?
А Двійкове дерево пошуку це дерево, яке дотримується певного порядку розташування елементів, тоді як бінарне дерево не дотримується жодного порядку. У бінарному дереві пошуку значення лівого вузла має бути меншим за батьківський вузол, а значення правого вузла має бути більшим за батьківський вузол.
Розберемо концепцію бінарного дерева пошуку на прикладах.

На наведеному вище малюнку ми бачимо, що значення кореневого вузла дорівнює 15, що більше, ніж значення всіх вузлів у лівому піддереві. Значення кореневого вузла менше, ніж значення всіх вузлів правого піддерева. Тепер ми переходимо до лівого дочірнього елемента кореневого вузла. 10 більше за 8 і менше за 12; він також задовольняє властивості бінарного дерева пошуку. Тепер ми переходимо до правого дочірнього елемента кореневого вузла; значення 20 більше за 17 і менше за 25; він також задовольняє властивості бінарного дерева пошуку. Таким чином, ми можемо сказати, що показано вище дерево є бінарним деревом пошуку.
Тепер, якщо ми змінимо значення 12 на 16 у наведеному вище двійковому дереві, ми маємо з’ясувати, чи є воно все ще бінарним деревом пошуку чи ні.

Значення кореневого вузла становить 15, що більше за 10, але менше за 16, тому воно не задовольняє властивості бінарного дерева пошуку. Тому це не бінарне дерево пошуку.
алгоритм к-нн
Операції над бінарним деревом пошуку
Ми можемо виконувати операції вставки, видалення та пошуку в бінарному дереві пошуку. Давайте розберемося, як виконується пошук у бінарному пошуку. Нижче показано бінарне дерево, на якому ми повинні виконати операцію пошуку:

Припустімо, що ми маємо знайти 10 у наведеному вище бінарному дереві. Щоб виконати двійковий пошук, ми розглянемо всі цілі числа в сортованому масиві. Спочатку ми створюємо повний список у просторі пошуку, і всі номери будуть існувати в просторі пошуку. Простір пошуку позначається двома покажчиками, тобто, початок і кінець. Масив наведеного вище бінарного дерева можна представити у вигляді

Спочатку ми обчислимо середній елемент і порівняємо середній елемент з елементом, який потрібно шукати. Середній елемент обчислюється за допомогою n/2. Значення n дорівнює 7; отже, середній елемент дорівнює 15. Середній елемент не дорівнює шуканому елементу, тобто 10.
Примітка. Якщо шуканий елемент менший за середній елемент, то пошук виконуватиметься в лівій половині; інакше пошук здійснюватиметься на правій половині. У випадку рівності елемент знайдений.
Оскільки елемент, який потрібно шукати, менший за середній елемент, тому пошук виконуватиметься в лівому масиві. Тепер пошук зменшено наполовину, як показано нижче:

Середній елемент у лівому масиві дорівнює 10, що дорівнює шуканому елементу.
Часова складність
У двійковому пошуку є n елементів. Якщо середній елемент не дорівнює шуканому елементу, тоді простір пошуку скорочується до n/2, і ми будемо продовжувати скорочувати простір пошуку на n/2, поки не знайдемо елемент. У цілому скорочення, якщо ми переходимо від n до n/2 до n/4 і так далі, тоді це займе log2n кроків.
Відмінності між бінарним деревом і бінарним деревом пошуку
char + int у java

| Основа для порівняння | Бінарне дерево | Двійкове дерево пошуку |
|---|---|---|
| Визначення | Бінарне дерево — це нелінійна структура даних, у якій вузол може мати щонайбільше двох дочірніх елементів, тобто вузол може мати 0, 1 або максимум двох дочірніх елементів. Двійкове дерево пошуку — це впорядковане бінарне дерево, у якому дотримується певний порядок для організації вузлів у дереві. | |
| Структура | Структура бінарного дерева полягає в тому, що перший вузол або найвищий вузол відомий як кореневий вузол. Кожен вузол бінарного дерева містить лівий і правий покажчики. Лівий покажчик містить адресу лівого піддерева, тоді як правий вказівник містить адресу правого піддерева. | Двійкове дерево пошуку — це один із типів бінарного дерева, яке має значення всіх вузлів у лівому піддереві, менше або дорівнює кореневому вузлу, а значення всіх вузлів у правому піддереві більше або дорівнює значення кореневого вузла. |
| Операції | Операції, які можна реалізувати на бінарному дереві, це вставка, видалення та обхід. | Двійкові дерева пошуку — це відсортовані двійкові дерева, які забезпечують швидке вставлення, видалення та пошук. Пошуки переважно реалізують двійковий пошук, оскільки всі ключі впорядковані в порядку. |
| види | Чотири типи двійкових дерев: повне двійкове дерево, повне двійкове дерево, ідеальне двійкове дерево та розширене двійкове дерево. | Існують різні типи бінарних дерев пошуку, наприклад дерева AVL, дерево Splay, дерева Tango тощо. |
