Нулі многочлена це дійсні, уявні або комплексні значення, коли ввести в поліном замість змінної результат стає нулем (як випливає з назви). Поліноми використовуються для моделювання деяких фізичних явищ, що відбуваються в реальному житті, вони дуже корисні при математичному описі ситуацій.

Нулі полінома — це всі значення x, які роблять поліном рівним нулю. Нулі полінома говорять нам про точки перетину x на графіку полінома. У цій статті ми поговоримо про нулі полінома, як їх знайти, факторна теорема тощо.

Зміст

• Що таке нулі поліномів?
• Нулі формули полінома
• Як знайти нуль полінома?
• Для лінійного полінома
• Для квадратичного полінома
• Для кубічного полінома
• Факторна теорема
• Зв'язок між нулями та коефіцієнтом
• Зв'язок між нулями та коефіцієнтом для квадратного рівняння
• Зв'язок між нулями та коефіцієнтом для кубічного рівняння
• Складання рівняння з нулями полінома
• Нулі в графіку поліномів
• Фундаментальна теорема лінійної алгебри
• Кратність кореня
• Статті за темою Нулі многочлена
• Зразки задач на нулі полінома
• Тренувальні задачі на нулі многочлена

Що таке нулі поліномів?

Для полінома P(x) ми говоримо, що x = a є нулем полінома, якщо P(a) = 0, і всі такі нулі полінома зазвичай називають нулями полінома. Наприклад, розглянемо f(x) = 3x – 12. Тепер помістимо x = 4 у поліном, тобто f(4) = 3×4 – 12 = 0. Таким чином, x = 4 є нулем полінома f( x) = 3x – 12.

Приклад: Для f(x) = x ³ – 6x ² + 11x – 6, х = 1 нуль?

рішення:

Щоб перевірити, чи є нулем f(x) = x, якщо x = 1³– 6x²+ 11x – 6 чи ні, поставте x = 1 у (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Таким чином, x = 1 є нулем f(x).

Нулі формули полінома

Для лінійного многочлена форми ax + b його нуль задано як x = -b/a.

Для квадратичного многочлена виду ax²+ bx + c, його нуль визначається як x = {- b ± √D}/2a, де D є дискримінантом, заданим b²– 4ac.

Як знайти нуль полінома?

Ми можемо знайти нулі полінома для різних типів поліномів за допомогою різних методів, які обговорюються нижче.

• Для лінійного полінома
• Для квадратичного полінома
• Для кубічного полінома

Для лінійного полінома

Для лінійних поліномів найпростіше знайти нуль. оскільки існує лише один нуль, і його також можна обчислити простою перестановкою полінома після прирівнювання полінома до 0.

Наприклад, знайдіть нуль для лінійного полінома f(x) = 2x – 7.

рішення:

Щоб знайти нуль f(x), прирівняйте f(x) до 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Для квадратичного полінома

Існують різні методи пошуку коренів або нулів квадратичного полінома, наприклад розщеплення середнього члена, квадратична формула, яка також відома як формула Шрі Дхарачар’я, і завершення квадрата, який дещо схожий на квадратичну формулу, оскільки квадратична формула виходить від доповнюючого квадрата для загального квадратного рівняння.

Дізнайтеся більше про розв’язування квадратних рівнянь або поліноми та як їх розв’язувати. У наведених нижче прикладах детально показано метод знаходження нулів квадратних поліномів.

Приклад 1: Знайдіть нулі для P(x) = x ² + 2x – 15.

відповідь:

х²+ 2x – 15 = 0

⇒ x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

значення xdxd

⇒ x = 3, -5

Приклад 2: Знайти вихідні нулі для P(x) = x ² – 16x + 64.

відповідь:

х²– 16x + 64 = 0

Порівнюючи з сокирою²+ bx + c = 0,

ми отримуємо, a = 1, b = -16 і c = 64.

Таким чином,

⇒ x = 8, 8

Для кубічного полінома

Щоб знайти нулі кубічної форми, існує багато способів, наприклад теорема про раціональний корінь і довге ділення разом. Один із методів знаходження коренів кубічного або будь-якого полінома вищого ступеня такий:

Крок 1: Використовуйте теорему про раціональний корень, щоб знайти можливі корені. тобто якщо поліном має раціональний корінь, це має бути ділення p/q, де p — ціла постійна, а q — старший коефіцієнт.

Крок 2: Знайшовши один корінь, розділіть многочлен на множник, утворений цим коренем, використовуючи довге ділення, і запишіть поліном у вигляді добутку частки та діленого.

крок 3: Якщо частка є квадратичним виразом, розв’яжіть її методами, згаданими вище для квадратичних поліномів. Якщо це не поліном 2-го ступеня, то повторюйте кроки 1 і 2, доки частка не стане поліномом 2-го ступеня.

крок 4: Результатом кроку 3 є необхідні множники, і, прирівнявши множник до 0, ми можемо знайти нулі полінома.

Приклад: знайдіть нулі кубічного многочлена p(x) = x ³ + 2х ² – 5x – 6.

рішення:

p(x) = x³+ 2х²– 5x – 6

Оскільки p/q = -6

Згідно з теоремою про раціональний корень, усі можливі раціональні корені півчлена є дільниками p/q.

Отже, дільники = ±1, ±2, ±3, ±6

x = -1, у p(x), ми отримуємо

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Таким чином, за теоремою про множники, x + 1 є множником p(x).

Таким чином, х³+ 2х²– 5x – 6 = (x+1)(x²+x – 6)

⇒ x³+ 2х²– 5x – 6 = (x+1)(x-2)(x+3)

Для нулів p(x) = 0,

Нулі p(x) є x = -1, x = 2 і x = -3.

Факторна теорема

Для полінома P(x) теорема про множники стверджує, що якщо x =a дорівнює нулю P(X), то тільки тоді x – a є множником P(x). тобто мають виконуватися обидві наступні умови.

• Якщо a є нулем P(x), то x−a буде фактором P(x)
• Якщо x−a є фактором P(x), то a буде нулем P(x)

У цьому можна переконатися, переглянувши попередні приклади. Факторна теорема може привести до деяких цікавих результатів, які є такими:

Результат 1: Якщо P(x) є поліномом ступеня n, а r є нулем P(x), то P(x) можна записати у такій формі:

P(x) = (x – r) Q(x)

Де Q(x) – це поліном ступеня n-1, який можна знайти шляхом ділення P(x) на (x – r).

Результат 2: Якщо P(x) = (x-r)Q(x) і x = t є нулем Q(x), то x = t також буде нулем P(x).

Щоб підтвердити вищезазначений факт,

Припустимо, t дорівнює нулю Q(x), що означає Q(t) = 0.

Ми знаємо, що r є нулем полінома P(x), де P(x) = (x – r) Q(x),

Тож нам потрібно перевірити, чи x = t також є нулем P(x), давайте покладемо x = t у P(x)

⇒ P(t) = (t – r) Q(t) = 0

Отже, x = t також є нулем P(x).

Отже, доведено.

Зв'язок між нулями та коефіцієнтом

Зв'язок між нулями і коефіцієнтом квадратного і кубічного рівнянь обговорюється нижче.

Зв'язок між нулями та коефіцієнтом для квадратного рівняння

Для квадратного рівняння виду ах²+ bx + c = 0, якщо двома нулями квадратного рівняння є α і β, то

• Сума кореня = α + β = -b/a
• Добуток коренів = α × β = c/a

Зв'язок між нулями та коефіцієнтом для кубічного рівняння

Якщо α, β і γ є коренем кубічного полінома ax³+ bx²+ cx + d = 0, то зв’язок між його нулями та коефіцієнтами має вигляд:

• a + b + c = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

Складання рівняння з нулями полінома

• Для квадратичного багаточлена з нулями α і β квадратичний поліном визначається як

х ² – (a + b)x + ab .

• Для кубічного полінома з трьома нулями α, β і γ кубічний поліном визначається як

х ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

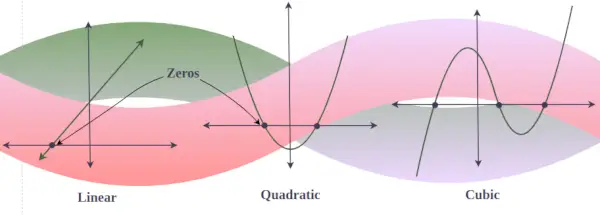
Нулі в графіку поліномів

На графіку будь-якого полінома y = f(x) дійсні нулі є точками, у яких графік перетинає або торкається осі x. (оскільки графік з уявним нулем ніколи не перетинає вісь x). Іншими словами, якщо існує 3 дійсних розв’язки кубічного полінома, то графік цього кубічного полінома тричі перетинає вісь х, але якщо існує лише один дійсний розв’язок для деякого кубічного полінома, то його графік лише перетинає вісь х. один раз.

Основна теорема лінійної алгебри

Якщо P(x) є поліномом ступеня n, тоді P(x) матиме рівно n нулів, деякі з яких можуть повторюватися.

підрядок рядок java

Це означає, що якщо ми перелічимо всі нулі та перерахуємо кожен k разів, коли k є його кратністю. У списку буде рівно n чисел. Це може бути корисно, оскільки може дати нам уявлення про те, скільки нулів має бути в поліномі. Тож ми можемо припинити шукати нулі, коли досягнемо необхідної кількості нулів.

Кратність кореня

Припустімо, що ми маємо поліном P(x) = 0, який розкладається на:

P(x) = (x – r) ^k (x – a) ^м

Якщо r є нулем багаточлена, а показник степеня в його члені, що дає корінь, дорівнює k, тоді ми говоримо, що r має кратність k . Часто називають нулі з кратністю 1 простий нулі та нулі кратності 2 називаються подвійними коренями многочлена.

Приклад: P(x) — поліном 5-го ступеня, розкладений на множники. Перелічіть корені та їх кратність.

P(x) = 5x ⁵ −20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x−2) ³

рішення:

Дано P(x) = 5(x+1)²(x−2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Щоб знайти нулі, P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Зверніть увагу, що -1 зустрічається двічі як нуль, тому його кратність дорівнює 2, а кратність нуля 2 дорівнює 3.

Статті за темою Нулі многочлена

• Поліном
• Корені квадратного рівняння
• Алгебраїчний вираз

Зразки задач на нулі полінома

Проблема 1: враховуючи, що x = 2 є нулем P(x) = x ³ +2x ² −5x−6. Знайдіть інші два нулі.

рішення:

З фундаментальної теореми, яку ми вивчали раніше, ми можемо сказати, що P(x) матиме 3 нулі, оскільки це поліном трьох ступенів. Один із них х = 2.

Отже, ми можемо переписати P(x),

P(x) = (x – 2) Q(x)

Щоб знайти інші два нулі, нам потрібно знайти Q(x).

Q(x) можна знайти, поділивши P(x) на (x-2).

Після поділу Q(x) виходить,

Q(x) = x²+ 4x + 3

Решта два нулі можна дізнатися з цього,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1(x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

х = -1, -3

Таким чином, інші два нулі є x = -1 і x = -3.

Задача 2: враховуючи, що x = r є нулем многочлена, знайти інші нулі полінома.

P(x) = x ³ -6x ² −16x; r = −2

рішення:

Ми знаємо, що x = -2 є нулем,

Отже, P(x) можна переписати як P(x) = (x + 2) Q(x) {За допомогою алгоритму ділення}

Тепер, щоб знайти Q(x), ми робимо те ж саме, що і в попередньому питанні, ділимо P(x) на (x + 2).

Ми отримуємо,

Q(x) = x²– 8 разів

Тепер, щоб знайти інші два нулі, розкладіть Q(x) на множники

Q(x) = x (x – 8) = 0

Отже, нулі х = 0, 8.

Отже, маємо три нулі, х = -2, 0, 8.

Задача 3: Знайдіть нулі многочлена 4х ³ -3x ² -25x-6 = 0

рішення:

Трюк розв'язувати поліноміальні рівняння третього ступеня,

Знайдіть найменше ціле число, яке може зробити значення полінома 0, починаючи з 1,-1,2 і так далі...

ми знаходимо, що для x = -2 ми отримуємо, що значення виразу дорівнює нулю.

Отже, один із коренів дорівнює -2.

Відповідно до факторної теореми, якщо a є одним із нулів полінома, отже (x-a) є фактором даного полінома.

Таким чином, за цим {x – (-2)} = (x+2) є множник POF над поліномом.

Отримуємо квадратне рівняння і там вже є нулі.

(4x²-11x-3)(x+2) = 0

Розкладіть квадратне рівняння на множники,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

х = -2, х = 3, х = -1/4

Завдання 4: Знайдіть нулі многочлена 4х ⁶ – 16x ⁴ = 0

рішення:

Поліном має ступінь до 6, отже, існує 6 нулів полінома.

4x⁴(х²-4) = 0

4x⁴(х²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Отже, x= 0, 0, 0, 0, 2, -2

Завдання 5: Знайти нулі функції полінома f(x) = x ³ – 2 рази ² – 5x + 6

рішення:

Щоб знайти нулі цього многочлена, покладемо f(x) = 0 і розв’яжемо x:

f(x) = x³– 2 рази²– 5x + 6 = 0

Оскільки d/a = 6

Згідно з теоремою про раціональний корень, усі можливі раціональні корені півчлена:

Дільники d/a = ±1, ±2, ±3, ±6

x = 1, у p(x), ми отримуємо

f(1) = (1)³– 2(1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Таким чином, за факторною теоремою, x – 1 є фактором p(x).

Таким чином, х³+ 2х²– 5x – 6 = (x-1)(x²-x – 6)

х³+ 2х²– 5x – 6 = (x-1)(x+2)(x-3)

Для нулів p(x) = 0,

Нулі p(x) є x = 1, x = -2 і x = 3.

Тренувальні задачі на нулі многочлена

1. Знайти всі нулі многочлена f(x) = x ³ – 6x ² + 11x – 6

2. Визначити всі нулі многочлена g(x) = 2x ⁴ – 7 разів ³ + 3х ² + 4x – 4

3. Знайти нулі многочлена h(x) = x ⁵ – 3 рази ⁴ + 2х ³ – 6x ² + x + 2

4. Визначити всі нулі многочлена p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

Поширені запитання щодо нулів полінома

Що таке нулі полінома?

Ці такі дійсні значення, оскільки значення полінома стає 0, тобто якщо p(x) є поліномом, а p(a) = 0, то x = a є нулем p(x).

Як знайти нулі полінома?

Існують різні методи для різних поліномів для знаходження нулів, наприклад для квадратичного розливу середнього члена та квадратичної формули. Для лінійного простого перегрупування змінних і для кубічного ми використовуємо комбінацію теореми про раціональний корень, довгого ділення, теореми про множники та теореми про залишки.

Чи може поліном мати більше одного нуля?

Так, поліном може мати більше одного нуля, насправді поліном n ступенів може мати щонайбільше n дійсних нулів.

Що таке кратність нуля полінома?

У процесі розкладання на множники один множник або один нуль полінома, а потім кілька разів з’являється множник або нуль, що називається кратністю цього кореня.

Що таке фундаментальна теорема алгебри?

Основна теорема алгебри стверджує, що якщо P(x) є поліномом ступеня n, тоді P(x) матиме рівно n нулів, деякі з яких можуть повторюватися.

Чи завжди многочлен зі ступенем n має n дійсних коренів?

Ні, поліном ступеня n не завжди має n дійсних коренів, оскільки деякі корені можуть бути уявними або комплексними числами.

Що таке ступінь нульового полінома?

Степінь нульового полінома дорівнює нулю.

verilog завжди