Z-SCORE У СТАТИСТИЦІ

Z-Score у статистиці це вимірювання того, скільки стандартних відхилень має точка даних від середнього значення розподілу. Давайте знайдемо z-оцінку в статистиці. Z-показник, що дорівнює 0, означає, що оцінка точки даних така сама, як і середня оцінка. Позитивний z-показник вказує на те, що точка даних вище середнього, тоді як негативний z-показник вказує на те, що точка даних нижче середнього.

Формула для обчислення z-показника така: z = (x – μ)/ p

Де:

x: є тестовим значенням
м: є середнім
в: є стандартним значенням

У цій статті ми обговоримо такі поняття:

Зміст

Що таке Z-Score?
Як розрахувати Z-показник?
Характеристики Z-Score
Обчисліть викиди за допомогою значення Z-показника
Реалізація Z-Score в Python
Застосування Z-Score
Z-показники проти стандартного відхилення
Чому Z-оцінки називаються стандартними?

Що таке Z-Score?

Z-оцінка, також відома як стандартна оцінка, повідомляє нам про відхилення точки даних від середнього, виражаючи його через стандартні відхилення вище або нижче середнього. Це дає нам уявлення про те, наскільки далека точка даних від середнього значення. Таким чином, Z-Score вимірюється в термінах стандартного відхилення від середнього. Наприклад, Z-оцінка 2 означає, що значення на 2 стандартних відхилення від середнього. Щоб використовувати z-показник, нам потрібно знати середнє значення сукупності (μ), а також стандартне відхилення сукупності (σ).

Формула для Z-оцінки

Z-показник можна розрахувати за такою формулою.

mylivecricket для живого крикету

z = (X – μ) / с

де,

z = Z-показник
X = значення елемента
μ = Середнє значення населення
σ = стандартне відхилення сукупності

Як розрахувати Z-показник?

Нам надано середнє значення генеральної сукупності (μ), стандартне відхилення генеральної сукупності (σ) і спостережене значення (x) у постановці задачі, замінюючи його в рівняння Z-показника, що дає нам значення Z-показника. Залежно від того, позитивний чи негативний Z-показник, ми можемо використовувати позитивна Z-таблиця або негативна Z-таблиця доступні онлайн або на звороті вашого підручника зі статистики в додатку.

приклад 1:

Ви складаєте іспит GATE і отримуєте 500 балів. Середній бал GATE становить 390, а стандартне відхилення – 45. Наскільки добре ви отримали результати тесту порівняно із середнім учасником тесту?

рішення:

Наступні дані легко доступні у наведеному вище питанні

Необроблений бал/спостережуване значення = X = 500

Середній бал = μ = 390

Стандартне відхилення = σ = 45

Застосовуючи формулу z-оцінки,

z = (X – μ) / с

z = (500 – 390) / 45

z = 110 / 45 = 2,44

Це означає, що ваш z-показник є 2.44 .

Оскільки Z-показник позитивний 2,44, ми будемо використовувати позитивну Z-таблицю.

Тепер давайте подивимося Z Таблиця (CC-BY), щоб дізнатися, наскільки добре ви отримали результати порівняно з іншими учасниками тестування.

Виконайте наведену нижче інструкцію, щоб знайти ймовірність із таблиці.

тут, z-оцінка = 2,44, котрий i nвказує, що точка даних на 2,44 стандартного відхилення вище середнього.

По-перше, відобразіть перші дві цифри 2.4 на осі Y.
Потім вздовж осі X, карта 0,04
З’єднайте обидві осі. Перетин цих двох надасть вам кумулятивну ймовірність, пов’язану зі значенням Z-показника, який ви шукаєте

[Ця ймовірність представляє площу під стандартною нормальною кривою ліворуч від Z-показника]

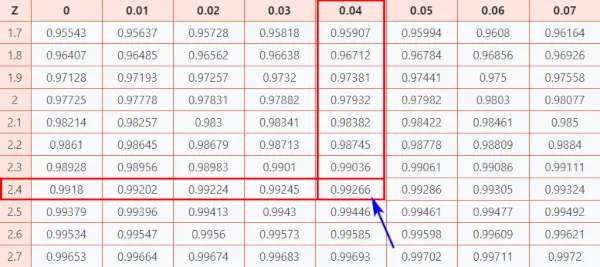
Таблиця нормального розподілу

В результаті ви отримаєте кінцеве значення, яке є 0,99266 .

суміжні кути

Тепер нам потрібно порівняти наш початковий бал 500 на іспиті GATE із середнім балом групи. Для цього нам потрібно перетворити кумулятивну ймовірність, пов’язану з Z-показником, у відсоткове значення.

0,99266 × 100 = 99,266%

Нарешті, ви можете сказати, що виступили майже добре 99% інших учасників тестування.

Приклад 2 : Яка ймовірність того, що учень отримає від 350 до 400 балів (із середнім балом μ 390 і стандартним відхиленням σ 45)?

рішення:

Мінімальна оцінка = X₁= 350

Максимальний бал = X₂= 400

Застосовуючи формулу z-оцінки,

с₁= (X1 – m) / с
if і else в bash

с₁= (350 – 390) / 45

с₁= -40 / 45 = -0,88

с₂= (X₂– м) / стор

z2 = (400 – 390) / 45

с₂= 10 / 45 = 0,22

Оскільки z1 від'ємне, нам доведеться дивитися на від'ємне значення Z-таблиця і знаходимо, що кумулятивна ймовірність p1, перша ймовірність, дорівнює 0,18943 .

с₂є позитивним, тому ми використовуємо позитивну Z-таблицю, яка дає кумулятивну ймовірність p₂з 0,58706 .

Остаточна ймовірність обчислюється шляхом віднімання p1 від p₂:

p = p₂– стор₁

p = 0,58706 – 0,18943 = 0,39763

Імовірність того, що студент набере від 350 до 400 балів, становить 39,763% (0,39763 * 100).

Характеристики Z-Score

Величина Z-показника відображає, наскільки далека точка даних знаходиться від середнього значення з точки зору стандартних відхилень.
Елемент, який має z-оцінку менше 0, означає, що елемент менший за середнє.
Z-показники дозволяють порівнювати точки даних з різних розподілів.
Елемент, який має z-оцінку більше 0, означає, що елемент перевищує середнє значення.
Елемент, який має z-оцінку, рівну 0, означає, що елемент дорівнює середньому значенню.
Елемент, який має z-показник, що дорівнює 1, означає, що елемент на 1 стандартне відхилення перевищує середнє; z-показник, що дорівнює 2, на 2 стандартні відхилення більше середнього значення тощо.
Елемент, який має z-показник, що дорівнює -1, означає, що елемент на 1 стандартне відхилення менше середнього; z-показник, що дорівнює -2, на 2 стандартні відхилення менше середнього значення тощо.
Якщо кількість елементів у даному наборі велика, то приблизно 68% елементів мають z-показник від -1 до 1; близько 95% мають z-показник від -2 до 2; приблизно 99% мають z-показник від -3 до 3. Це відоме як емпіричне правило, яке визначає відсоток даних у межах певних стандартних відхилень від середнього в нормальному розподілі, як показано на зображенні нижче

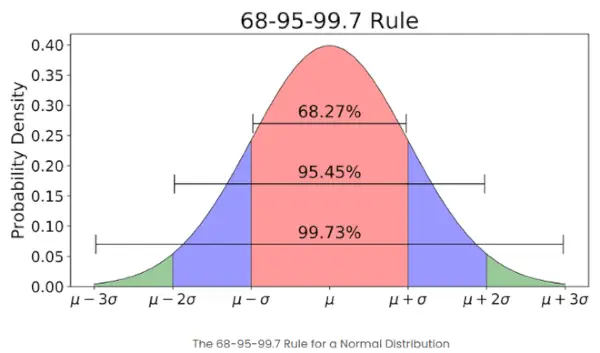
Емпіричне правило нормального розподілу

Обчисліть викиди за допомогою значення Z-показника

Ми можемо обчислити викиди в даних, використовуючи значення z-показника точок даних. Кроки, щоб розглянути точку даних, що викидається, такі:

Спочатку ми збираємо набір даних, у якому хочемо побачити викиди
Ми обчислимо середнє значення та стандартне відхилення набору даних. Ці значення використовуватимуться для обчислення значення z-показника кожної точки даних.
Ми розрахуємо значення z-показника для кожної точки даних. Формула для розрахунку значення z-показника буде такою ж, як
Z = frac{{X – mu}}{{sigma}}
де X — точка даних, μ — середнє значення даних, а σ — стандартне відхилення набору даних.
Ми визначимо граничне значення для z-показника, після якого точка даних може вважатися викидом. Це граничне значення є гіперпараметром, який ми вирішуємо залежно від нашого проекту.
Точка даних, значення z-показника якого перевищує 3, означає, що ця точка даних не належить до 99,73% точки набору даних.
Будь-яка точка даних, z-показник якої перевищує наше прийняте граничне значення, вважатиметься викидом.

перевірити: Оцінка Z для виявлення викидів

Реалізація Z-Score в Python

Ми можемо використовувати Python для обчислення значення z-показника точок даних у наборі даних. Крім того, ми будемо використовувати бібліотеку numpy для обчислення середнього значення та стандартного відхилення набору даних.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Викиди в наборі даних є {викиди}')>

Вихід:

Z-показник: [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Викиди в наборі даних [150]

Застосування Z-Score

Z-показники часто використовуються для масштабування функцій, щоб привести різні функції до спільного масштабу. Функції нормалізації гарантують, що вони мають нульове середнє значення та одиничну дисперсію, що може бути корисним для певних алгоритмів машинного навчання, особливо тих, які покладаються на вимірювання відстані.
Z-оцінки можна використовувати для виявлення викидів у наборі даних. Точки даних із Z-показниками, що перевищують певний порог (зазвичай 3 стандартні відхилення від середнього), можуть вважатися викидами.
Z-показники можуть використовуватися в алгоритмах виявлення аномалій, щоб визначити випадки, які значно відхиляються від очікуваної поведінки.
Z-оцінки можна застосувати для перетворення викривлених розподілів у більш нормальні розподіли.
Під час роботи з регресійними моделями можна аналізувати Z-показники залишків, щоб перевірити гомоскедастичність (постійну дисперсію залишків).
Z-оцінки можна використовувати для масштабування ознак, дивлячись на їхні стандартні відхилення від середнього.

Z-показники проти стандартного відхилення

Z- Оцінка сортування оболонки	Стандартне відхилення
Перетворення необроблених даних у стандартизовану шкалу. питання співбесіди мовою java	Вимірює ступінь варіації або дисперсії в наборі значень.
Спрощує порівняння значень із різних наборів даних, оскільки вони забирають вихідні одиниці вимірювання.	Стандартне відхилення зберігає оригінальні одиниці вимірювання, що робить його менш придатним для прямого порівняння між наборами даних з різними одиницями.
Укажіть, наскільки далека точка даних знаходиться від середнього значення в термінах стандартних відхилень, надаючи міру відносної позиції точки даних у розподілі	Виражається в тих самих одиницях, що й вихідні дані, забезпечуючи абсолютну міру того, наскільки значення розповсюджені навколо середнього

Z- Оцінка

сортування оболонки

Стандартне відхилення

Перетворення необроблених даних у стандартизовану шкалу.

питання співбесіди мовою java

Вимірює ступінь варіації або дисперсії в наборі значень.

Спрощує порівняння значень із різних наборів даних, оскільки вони забирають вихідні одиниці вимірювання.

Стандартне відхилення зберігає оригінальні одиниці вимірювання, що робить його менш придатним для прямого порівняння між наборами даних з різними одиницями.

Укажіть, наскільки далека точка даних знаходиться від середнього значення в термінах стандартних відхилень, надаючи міру відносної позиції точки даних у розподілі

Виражається в тих самих одиницях, що й вихідні дані, забезпечуючи абсолютну міру того, наскільки значення розповсюджені навколо середнього

перевірити: Таблиця Z-оцінки

Чому Z-оцінки називаються стандартними?

Z-оцінки також відомі як стандартні оцінки, оскільки вони стандартизують значення випадкової змінної. Це означає, що список стандартизованих балів має середнє значення 0 і стандартне відхилення 1,0. Z-оцінки також дозволяють порівнювати оцінки за різними видами змінних. Це пояснюється тим, що вони використовують відносну позицію, щоб прирівняти бали за різними змінними чи розподілами.

Z-показники часто використовуються для порівняння змінної зі стандартним нормальним розподілом (з μ = 0 і σ = 1).

Z-Score у статистиці – поширені запитання

Яке значення позитивних і негативних Z-показників?

Позитивні Z-показники вказують на значення вище середнього, тоді як негативні Z-показники вказують на значення, нижчі за середнє. Знак відображає напрямок відхилення від середнього.

Що означає Z-показник 0?

Z-показник 0 означає, що значення точки даних точно відповідає середньому значенню набору даних. Це означає, що точка даних не вище і не нижче середнього.

Що таке правило 68-95-99.7 стосовно Z-показників?

Правило 68-95-99.7, також відоме як Емпіричне правило, стверджує, що:

Близько 68% даних знаходяться в межах 1 стандартного відхилення від середнього значення.
Близько 95% знаходиться в межах 2 стандартних відхилень.
Близько 99,7% знаходиться в межах 3 стандартних відхилень.

Чи можна використовувати Z-показники для ненормальних розподілів?

Z-показники базуються на припущенні, що дані мають нормальний розподіл. Однак на практиці Z-показники є корисними для даних, які відповідають нормальному розподілу. Хоча Z-показники можуть бути розраховані для будь-якого розподілу, їх інтерпретація стає менш надійною та простою, коли мова йде про ненормально розподілені дані.

Як можна застосувати Z-Scores у реальних ситуаціях?

Z-Scores мають різні застосування, наприклад у фінансах для аналізу портфоліо, освіті для стандартизованого тестування, здоров’ї для клінічної оцінки тощо. Вони забезпечують стандартизовану міру для порівняння та інтерпретації даних.