У цій статті ми обговоримо обхід дерева в структурі даних. Термін «обхід дерева» означає обхід або відвідування кожного вузла дерева. Існує єдиний спосіб обходу лінійної структури даних, наприклад пов’язаного списку, черги та стеку. У той час як існує кілька способів обійти дерево, які перераховані нижче:

• Обхід попереднього замовлення
• Обхід у порядку
• Обхід поштового замовлення

Отже, у цій статті ми обговоримо перелічені вище прийоми обходу дерева. Тепер давайте почнемо обговорювати шляхи обходу дерева.

Обхід попереднього замовлення

Ця техніка відповідає політиці «root left right». Це означає, що відвідується перший кореневий вузол, після чого рекурсивно проходить ліве піддерево, і, нарешті, рекурсивно проходить праве піддерево. Оскільки кореневий вузол обходиться перед (або перед) лівим і правим піддеревом, це називається обходом попереднього порядку.

Таким чином, у попередньому обході кожен вузол відвідується перед обома його піддеревами.

Застосування обходу попереднього замовлення включають:

• Він використовується для створення копії дерева.
• Його також можна використовувати для отримання префіксного виразу дерева виразів.

Алгоритм

 Until all nodes of the tree are not visited Step 1 - Visit the root node Step 2 - Traverse the left subtree recursively. Step 3 - Traverse the right subtree recursively. 

приклад

Тепер давайте розглянемо приклад техніки обходу попереднього замовлення.

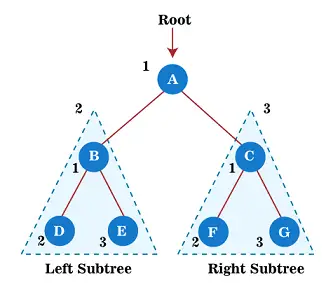
Тепер почніть застосовувати обхід попереднього замовлення до дерева вище. Спочатку ми проходимо кореневий вузол А; після цього перейдіть до його лівого піддерева Б , який також буде пройдено в попередньому порядку.

Отже, для лівого піддерева B, спочатку, кореневий вузол Б проходить сам; після цього його ліве піддерево Д пройдено. Оскільки вузол Д не має дітей, перейдіть до правого піддерева І . Оскільки вузол E також не має дітей, обхід лівого піддерева кореневого вузла A завершено.

методи java

Тепер перейдіть до правого піддерева кореневого вузла A, тобто C. Отже, для правого піддерева C спочатку кореневий вузол C подолав себе; після цього його ліве піддерево Ф пройдено. Оскільки вузол Ф не має дітей, перейдіть до правого піддерева Г . Оскільки вузол G також не має дітей, обхід правого піддерева кореневого вузла A завершено.

Тому обходяться всі вузли дерева. Отже, вихід попереднього обходу вищевказаного дерева -

A → B → D → E → C → F → G

Щоб дізнатися більше про обхід попереднього замовлення в структурі даних, ви можете перейти за посиланням Обхід попереднього замовлення .

Обхід поштового замовлення

Ця техніка відповідає політиці «лівий-правий корінь». Це означає, що обходиться перше ліве піддерево кореневого вузла, потім рекурсивно проходить праве піддерево і, нарешті, обходиться кореневий вузол. Оскільки кореневий вузол обходиться після (або після) лівого та правого піддерева, це називається обходом постпорядку.

Отже, у постпорядковому обході кожен вузол відвідується після обох своїх піддерев.

Застосування обходу після замовлення включають:

байтів python у рядок

• Використовується для видалення дерева.
• Його також можна використовувати для отримання постфіксного виразу дерева виразів.

Алгоритм

 Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Traverse the right subtree recursively. Step 3 - Visit the root node. 

приклад

Тепер давайте розглянемо приклад техніки обходу після замовлення.

Тепер почніть застосовувати обхід після замовлення до вищевказаного дерева. Спочатку ми проходимо ліве піддерево B, яке буде проходити в постпорядку. Після цього ми пройдемо праве піддерево C після замовлення. І, нарешті, кореневий вузол вищезгаданого дерева, тобто А , пройдено.

Отже, для лівого піддерева B, спочатку його ліве піддерево Д пройдено. Оскільки вузол Д не має дочірніх елементів, перейдіть до правого піддерева І . Оскільки вузол E також не має дітей, перейдіть до кореневого вузла Б. Після проходження вузла B, обхід лівого піддерева кореневого вузла A завершено.

Тепер перейдіть до правого піддерева кореневого вузла A, тобто C. Отже, для правого піддерева C спочатку його ліве піддерево Ф пройдено. Оскільки вузол Ф не має дочірніх елементів, перейдіть до правого піддерева Г . Оскільки вузол G також не має дітей, отже, нарешті, кореневий вузол правого піддерева, тобто C, пройдено. Обхід правого піддерева кореневого вузла A завершено.

Нарешті, пройдіть кореневий вузол даного дерева, тобто А . Після обходу кореневого вузла обхід заданого дерева після замовлення завершується.

Тому обходяться всі вузли дерева. Таким чином, результат обходу вищезазначеного дерева в порядку:

D → E → B → F → G → C → A

Щоб дізнатися більше про обхід після замовлення в структурі даних, ви можете перейти за посиланням Обхід поштового замовлення .

Обхід у порядку

Ця техніка відповідає політиці «лівий корінь правий». Це означає, що перше ліве піддерево відвідується після проходження цього кореневого вузла, і, нарешті, обхід правого піддерева. Оскільки кореневий вузол обходиться між лівим і правим піддеревом, він називається обходом у порядку.

gimp видалення фону

Отже, під час обходу в порядку кожен вузол відвідується між його піддеревами.

Програми обходу порядку включають:

• Він використовується для отримання вузлів BST у порядку зростання.
• Його також можна використовувати для отримання префіксного виразу дерева виразів.

Алгоритм

 Until all nodes of the tree are not visited Step 1 - Traverse the left subtree recursively. Step 2 - Visit the root node. Step 3 - Traverse the right subtree recursively. 

приклад

Тепер давайте розглянемо приклад техніки обходу Inorder.

Тепер почніть застосовувати обхід у порядку до вищевказаного дерева. Спочатку ми проходимо ліве піддерево Б які будуть пройдені по порядку. Після цього ми пройдемо кореневий вузол А . І, нарешті, праве піддерево C проходить по порядку.

Отже, для лівого піддерева Б , спочатку його ліве піддерево Д пройдено. Оскільки вузол Д не має дітей, тому після його обходу node Б буде пройдено, і, нарешті, праве піддерево вузла B, тобто І , пройдено. Вузол E також не має дітей; отже, обхід лівого піддерева кореневого вузла A завершено.

Після цього пройдіть кореневий вузол даного дерева, тобто А .

Нарешті, перейдіть до правого піддерева кореневого вузла A, тобто C. Отже, для правого піддерева C; спочатку його ліве піддерево Ф пройдено. Оскільки вузол Ф не має дітей, вузол C буде пройдено, і, нарешті, праве піддерево вузла C, тобто Г , пройдено. Вузол G також не має дітей; отже, обхід правого піддерева кореневого вузла A завершено.

рівність об’єктів у java

Після проходження всіх вузлів дерева обхід у порядку даного дерева завершується. Вихід обходу вищевказаного дерева в порядку:

D → B → E → A → F → C → G

Щоб дізнатися більше про порядок проходження в структурі даних, ви можете перейти за посиланням Обхід порядку .

Складність техніки обходу дерева

Часова складність методів обходу дерева, про які йшлося вище, така O(n) , де 'n' це розмір бінарного дерева.

У той час як космічна складність обговорюваних вище методів обходу дерев є O(1) якщо ми не беремо до уваги розмір стека для викликів функцій. В іншому випадку космічна складність цих прийомів є O(h) , де 'h' це висота дерева.

Реалізація обходу дерева

Тепер давайте подивимося реалізацію розглянутих вище методів за допомогою різних мов програмування.

програма: Напишіть програму для реалізації техніки обходу дерева на C.

 #include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root->left); printf(' %d ', root->element); traverseInorder(root->right); } /*function to traverse the nodes of binary tree in postorder*/ void traversePostorder(struct node* root) { if (root == NULL) return; traversePostorder(root->left); traversePostorder(root->right); printf(' %d ', root->element); } int main() { struct node* root = createNode(36); root->left = createNode(26); root->right = createNode(46); root->left->left = createNode(21); root->left->right = createNode(31); root->left->left->left = createNode(11); root->left->left->right = createNode(24); root->right->left = createNode(41); root->right->right = createNode(56); root->right->right->left = createNode(51); root->right->right->right = createNode(66); printf('
 The Preorder traversal of given binary tree is -
'); traversePreorder(root); printf('
 The Inorder traversal of given binary tree is -
'); traverseInorder(root); printf('
 The Postorder traversal of given binary tree is -
'); traversePostorder(root); return 0; } 

Вихід

програма: Напишіть програму для реалізації техніки обходу дерева на C#.

злиття, сортування java

 using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); Console.Write(node.value + ' '); traverseInorder(node.right); } void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); Console.Write(node.value + ' '); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(37); bt.root.left = new Node(27); bt.root.right = new Node(47); bt.root.left.left = new Node(22); bt.root.left.right = new Node(32); bt.root.left.left.left = new Node(12); bt.root.left.left.right = new Node(25); bt.root.right.left = new Node(42); bt.root.right.right = new Node(57); bt.root.right.right.left = new Node(52); bt.root.right.right.right = new Node(67); Console.WriteLine('The Preorder traversal of given binary tree is - '); bt.traversePreorder(); Console.WriteLine(); Console.WriteLine('The Inorder traversal of given binary tree is - '); bt.traverseInorder(); Console.WriteLine(); Console.WriteLine('The Postorder traversal of given binary tree is - '); bt.traversePostorder(); } } 

Вихід

програма: Напишіть програму для реалізації методів обходу дерева на C++.

 #include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node-&gt;element = val; Node-&gt;left = NULL; Node-&gt;right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout&lt;<' '<element<left); traversepreorder(root->right); } /*function to traverse the nodes of binary tree in Inorder*/ void traverseInorder(struct node* root) { if (root == NULL) return; traverseInorder(root-&gt;left); cout&lt;<' '<element<right); } *function to traverse the nodes of binary tree in postorder* void traversepostorder(struct node* root) { if (root="=" null) return; traversepostorder(root->left); traversePostorder(root-&gt;right); cout&lt;<' '<element<left="createNode(28);" root->right = createNode(48); root-&gt;left-&gt;left = createNode(23); root-&gt;left-&gt;right = createNode(33); root-&gt;left-&gt;left-&gt;left = createNode(13); root-&gt;left-&gt;left-&gt;right = createNode(26); root-&gt;right-&gt;left = createNode(43); root-&gt;right-&gt;right = createNode(58); root-&gt;right-&gt;right-&gt;left = createNode(53); root-&gt;right-&gt;right-&gt;right = createNode(68); cout&lt;<'
 the preorder traversal of given binary tree is -
'; traversepreorder(root); cout<<'
 inorder traverseinorder(root); postorder traversepostorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-6.webp" alt="Tree Traversal"> <p> <strong>Program:</strong> Write a program to implement tree traversal techniques in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class Tree { Node root; /* root of the tree */ Tree() { root = null; } /*function to print the nodes of given binary in Preorder*/ void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + &apos; &apos;); traversePreorder(node.left); traversePreorder(node.right); } /*function to print the nodes of given binary in Inorder*/ void traverseInorder(Node node) { if (node == null) return; traverseInorder(node.left); System.out.print(node.value + &apos; &apos;); traverseInorder(node.right); } /*function to print the nodes of given binary in Postorder*/ void traversePostorder(Node node) { if (node == null) return; traversePostorder(node.left); traversePostorder(node.right); System.out.print(node.value + &apos; &apos;); } void traversePreorder() { traversePreorder(root); } void traverseInorder() { traverseInorder(root); } void traversePostorder() { traversePostorder(root); } public static void main(String args[]) { Tree pt = new Tree(); pt.root = new Node(36); pt.root.left = new Node(26); pt.root.right = new Node(46); pt.root.left.left = new Node(21); pt.root.left.right = new Node(31); pt.root.left.left.left = new Node(11); pt.root.left.left.right = new Node(24); pt.root.right.left = new Node(41); pt.root.right.right = new Node(56); pt.root.right.right.left = new Node(51); pt.root.right.right.right = new Node(66); System.out.println(); System.out.println(&apos;The Preorder traversal of given binary tree is - &apos;); pt.traversePreorder(); System.out.println(&apos;
&apos;); System.out.println(&apos;The Inorder traversal of given binary tree is - &apos;); pt.traverseInorder(); System.out.println(&apos;
&apos;); System.out.println(&apos;The Postorder traversal of given binary tree is - &apos;); pt.traversePostorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/17/tree-traversal-inorder-7.webp" alt="Tree Traversal"> <h2>Conclusion</h2> <p>In this article, we have discussed the different types of tree traversal techniques: preorder traversal, inorder traversal, and postorder traversal. We have seen these techniques along with algorithm, example, complexity, and implementation in C, C++, C#, and java.</p> <p>So, that&apos;s all about the article. Hope it will be helpful and informative to you.</p> <hr></'
></'></'></'>

Вихід

Після виконання наведеного вище коду результатом буде -

Висновок

У цій статті ми обговорили різні типи методів обходу дерева: обхід попереднього порядку, обхід у порядку та обхід після замовлення. Ми бачили ці методи разом із алгоритмом, прикладом, складністю та реалізацією в C, C++, C# та java.

Отже, це все про статтю. Сподіваюся, це буде для вас корисно та інформативно.