У цій статті ми обговоримо попередній обхід у структурі даних. Лінійні структури даних, такі як стек, масив, черга тощо, мають лише один спосіб обходу даних. Але в ієрархічній структурі даних, наприклад дерево , існує кілька способів перегляду даних.
Під час попереднього обходу спочатку відвідується кореневий вузол, потім ліве піддерево, а після цього – праве піддерево. Процес обходу попереднього порядку можна представити як -
root → left → right
Кореневий вузол завжди обходиться першим у попередньому обході, тоді як він є останнім елементом обходу після замовлення. Обхід попереднього порядку використовується для отримання префіксного виразу дерева.
Нижче наведено кроки для виконання попереднього замовлення:
- Спочатку відвідайте кореневий вузол.
- Потім перейдіть до лівого піддерева.
- Нарешті відвідайте праве піддерево.
Техніка обходу попереднього замовлення слідує за Корінь зліва направо політики. Сама назва попереднього порядку передбачає, що кореневий вузол буде проходити першим.
Алгоритм
Тепер розглянемо алгоритм обходу попереднього замовлення.
Step 1: Repeat Steps 2 to 4 while TREE != NULL Step 2: Write TREE -> DATA Step 3: PREORDER(TREE -> LEFT) Step 4: PREORDER(TREE -> RIGHT) [END OF LOOP] Step 5: END
Приклад обходу попереднього замовлення
Тепер давайте розглянемо приклад проходження попереднього замовлення. На прикладі буде легше зрозуміти процес обходу попереднього замовлення.
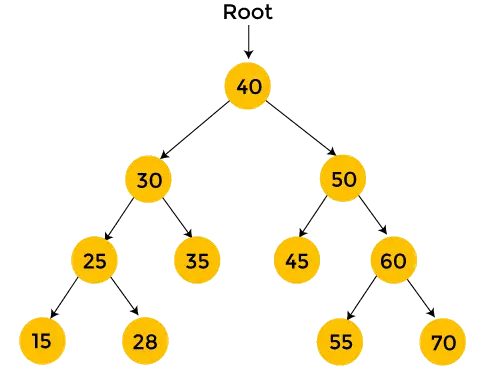
Вузли з жовтим кольором ще не відвідуються. Тепер ми обійдемо вузли вищезазначеного дерева за допомогою попереднього обходу.
- Почніть з кореневого вузла 40. По-перше, надрукувати 40 а потім рекурсивно пройти ліве піддерево.
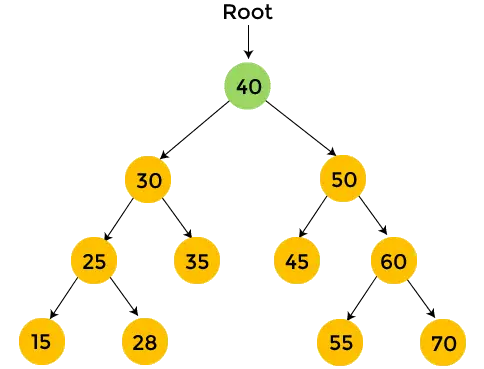
- Тепер перейдіть до лівого піддерева. Для лівого піддерева кореневий вузол дорівнює 30. Друк 30 , і перейдіть до лівого піддерева 30.
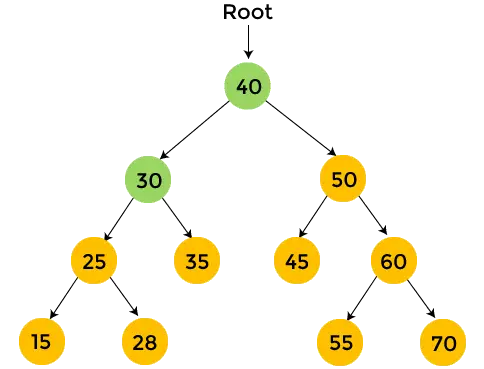
- У лівому піддереві 30 є елемент 25, отже надрукувати 25 , і пройдіть ліве піддерево 25.
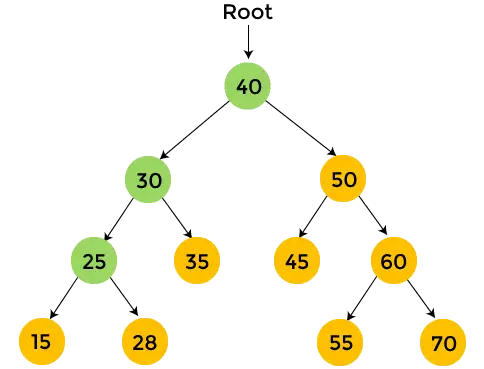
- У лівому піддереві 25 є елемент 15, а 15 не має піддерева. Так, друк 15 , і перейдіть до правого піддерева 25.
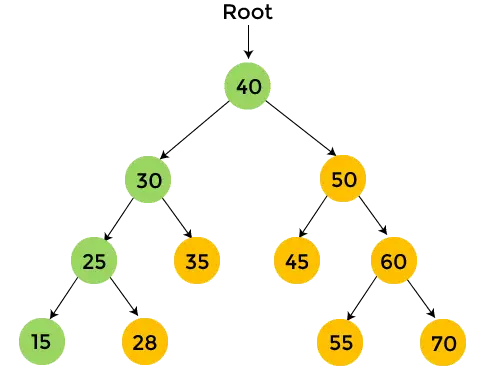
- У правому піддереві 25 є 28, а 28 не має піддерева. Так, друк 28 , і перейдіть до правого піддерева 30.
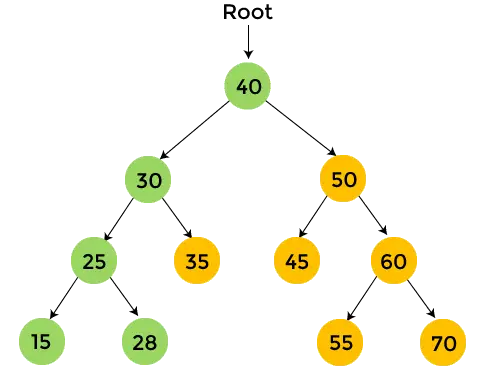
- У правому піддереві 30 є 35, яке не має піддерева. Так надрукувати 35 , і пройдіть праве піддерево 40.
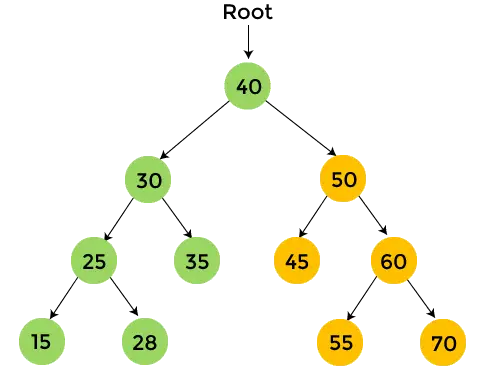
- У правому піддереві 40 є 50. Роздрукувати 50 , і пройдіть ліве піддерево 50.
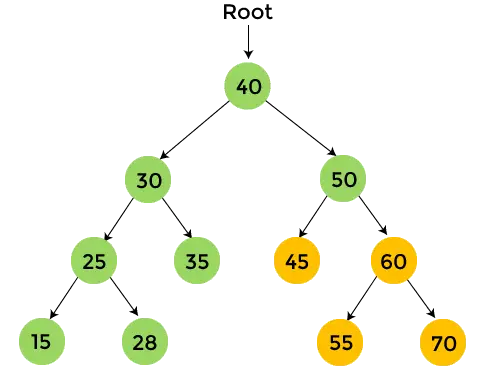
- У лівому піддереві 50 є 45, які не мають дочірніх елементів. Так, надрукувати 45 , і пройдіть праве піддерево 50.
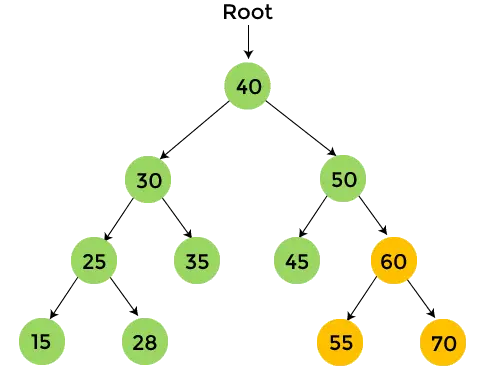
- У правому піддереві 50 є 60. Друк 60 і перетнути ліве піддерево 60.
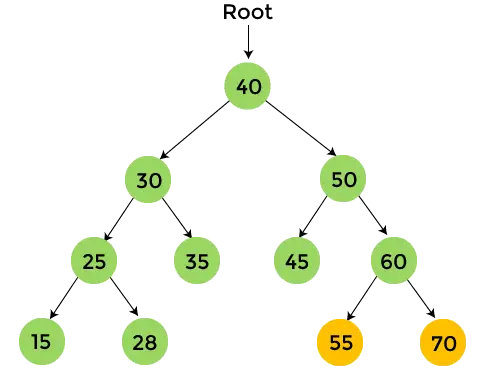
- У лівому піддереві 60 є 55, яке не має дочірніх елементів. Так, надрукувати 55 і перейдіть до правого піддерева 60.
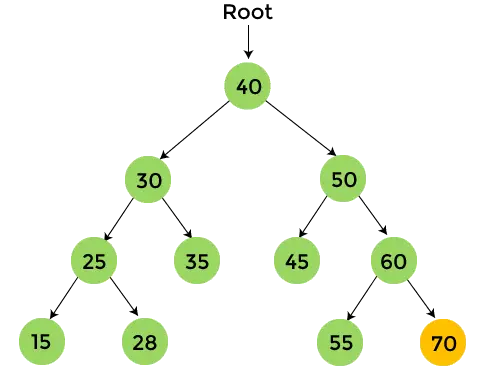
- У правому піддереві 60 є 70, які не мають дочірніх елементів. Так, надрукувати 70 і зупинити процес.
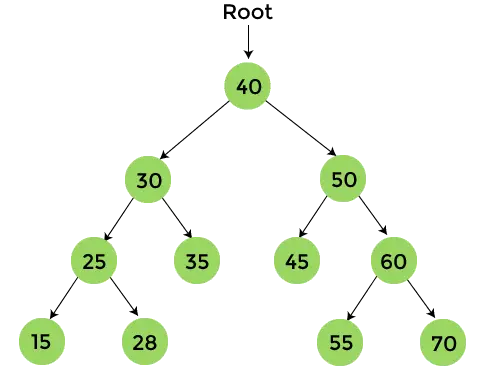
Після завершення обходу попереднього замовлення кінцевий результат -
40, 30, 25, 15, 28, 35, 50, 45, 60, 55, 70
Складність проходження Preorder
Часова складність обходу попереднього замовлення становить O(n) , де 'n' — розмір бінарного дерева.
У той час як просторова складність обходу попереднього замовлення є O(1) , якщо не враховувати розмір стека для викликів функцій. В іншому випадку складність обходу попереднього замовлення становить простір O(h) , де «h» — висота дерева.
Реалізація попереднього обходу
Тепер давайте подивимося реалізацію попереднього обходу в різних мовах програмування.
програма: Напишіть програму для реалізації попереднього обходу мовою C.
#include #include struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; printf(' %d ', root->element); traversePreorder(root->left); traversePreorder(root->right); } int main() { struct node* root = createNode(40); root->left = createNode(30); root->right = createNode(50); root->left->left = createNode(25); root->left->right = createNode(35); root->left->left->left = createNode(15); root->left->left->right = createNode(28); root->right->left = createNode(45); root->right->right = createNode(60); root->right->right->left = createNode(55); root->right->right->right = createNode(70); printf('
The Preorder traversal of given binary tree is -
'); traversePreorder(root); return 0; } Вихід
Після виконання наведеного вище коду результатом буде -

програма: Напишіть програму для реалізації попереднього обходу на C++.
#include using namespace std; struct node { int element; struct node* left; struct node* right; }; /*To create a new node*/ struct node* createNode(int val) { struct node* Node = (struct node*)malloc(sizeof(struct node)); Node->element = val; Node->left = NULL; Node->right = NULL; return (Node); } /*function to traverse the nodes of binary tree in preorder*/ void traversePreorder(struct node* root) { if (root == NULL) return; cout<<' '<element<left); traversepreorder(root->right); } int main() { struct node* root = createNode(39); root->left = createNode(29); root->right = createNode(49); root->left->left = createNode(24); root->left->right = createNode(34); root->left->left->left = createNode(14); root->left->left->right = createNode(27); root->right->left = createNode(44); root->right->right = createNode(59); root->right->right->left = createNode(54); root->right->right->right = createNode(69); cout<<'
the preorder traversal of given binary tree is -
'; traversepreorder(root); return 0; } < pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/25/preorder-traversal-14.webp" alt="Preorder Traversal"> <p> <strong>Program:</strong> Write a program to implement preorder traversal in C#.</p> <pre> using System; class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class BinaryTree { Node root; BinaryTree() { root = null; } void traversePreorder(Node node) { if (node == null) return; Console.Write(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traversePreorder() { traversePreorder(root); } static void Main() { BinaryTree bt = new BinaryTree(); bt.root = new Node(38); bt.root.left = new Node(28); bt.root.right = new Node(48); bt.root.left.left = new Node(23); bt.root.left.right = new Node(33); bt.root.left.left.left = new Node(13); bt.root.left.left.right = new Node(26); bt.root.right.left = new Node(43); bt.root.right.right = new Node(58); bt.root.right.right.left = new Node(53); bt.root.right.right.right = new Node(68); Console.WriteLine('Preorder traversal of given binary tree is - '); bt.traversePreorder(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/25/preorder-traversal-15.webp" alt="Preorder Traversal"> <p> <strong>Program:</strong> Write a program to implement preorder traversal in Java.</p> <pre> class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PreorderTraversal { Node root; PreorderTraversal() { root = null; } void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traversePreorder() { traversePreorder(root); } public static void main(String args[]) { PreorderTraversal pt = new PreorderTraversal(); pt.root = new Node(37); pt.root.left = new Node(27); pt.root.right = new Node(47); pt.root.left.left = new Node(22); pt.root.left.right = new Node(32); pt.root.left.left.left = new Node(12); pt.root.left.left.right = new Node(25); pt.root.right.left = new Node(42); pt.root.right.right = new Node(57); pt.root.right.right.left = new Node(52); pt.root.right.right.right = new Node(67); System.out.println(); System.out.println('Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println(); } } </pre> <p> <strong>Output</strong> </p> <p>After the execution of the above code, the output will be -</p> <img src="//techcodeview.com/img/ds-tutorial/25/preorder-traversal-16.webp" alt="Preorder Traversal"> <p>So, that's all about the article. Hope the article will be helpful and informative to you.</p> <hr></'
></'> Вихід
Після виконання наведеного вище коду результатом буде -

програма: Напишіть програму для реалізації попереднього обходу в Java.
class Node { public int value; public Node left, right; public Node(int element) { value = element; left = right = null; } } class PreorderTraversal { Node root; PreorderTraversal() { root = null; } void traversePreorder(Node node) { if (node == null) return; System.out.print(node.value + ' '); traversePreorder(node.left); traversePreorder(node.right); } void traversePreorder() { traversePreorder(root); } public static void main(String args[]) { PreorderTraversal pt = new PreorderTraversal(); pt.root = new Node(37); pt.root.left = new Node(27); pt.root.right = new Node(47); pt.root.left.left = new Node(22); pt.root.left.right = new Node(32); pt.root.left.left.left = new Node(12); pt.root.left.left.right = new Node(25); pt.root.right.left = new Node(42); pt.root.right.right = new Node(57); pt.root.right.right.left = new Node(52); pt.root.right.right.right = new Node(67); System.out.println(); System.out.println('Preorder traversal of given binary tree is - '); pt.traversePreorder(); System.out.println(); } } Вихід
Після виконання наведеного вище коду результатом буде -

Отже, це все про статтю. Сподіваюся, стаття буде для вас корисною та інформативною.











