Тригонометрія — важлива галузь математики, яка вивчає співвідношення між кутами та довжинами сторін прямокутного трикутника. Шість тригонометричних співвідношень або функцій — це синус, косинус, тангенс, косеканс і секанс, а тригонометричне відношення — це відношення між сторонами прямокутного трикутника. Функції синус, косинус і тангенс є трьома важливими тригонометричними функціями, оскільки інші три, тобто косеканс, секанс і котангенс, є функціями, зворотними функціям синуса, косинуса і тангенса відповідно.
- sin θ = протилежна сторона/гіпотенуза
- cos θ = прилегла сторона/гіпотенуза
- tan θ = протилежна сторона/прилегла сторона
- cosec θ = гіпотенуза/протилежна сторона
- сек θ = Гіпотенуза/прилегла сторона
- ліжечко θ = сусідня сторона/протилежна сторона
Функція тангенса — одна з 6 тригонометричних функцій, які використовуються в формули тригонометрії .
Зміст
Формула дотичної
Тангенс кута в прямокутному трикутнику - це відношення довжини протилежної сторони до довжини сторони, прилеглої до даного кута. Ми запишемо функцію тангенса як tan. Розглянемо прямокутний трикутник XYZ, один із гострих кутів якого дорівнює θ. Протилежною стороною є сторона, протилежна куту θ, а прилеглою стороною є сторона, яка прилягає до кута θ.
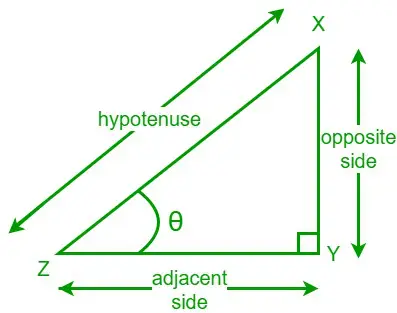
Тепер формула тангенса для даного кута θ є,
tan θ = протилежна сторона/прилегла сторона
Деякі основні формули дотичної
Функція тангенса в квадрантах
Функція тангенса додатна в першому і третьому квадрантах і від’ємна в другому і четвертому квадрантах.
- tan (2π + θ) = tan θ (1вулквадрант)
- tan (π – θ) = – tan θ (2ndквадрант)
- tan (π + θ) = tan θ (3rdквадрант)
- tan (2π – θ) = – tan θ (4тисквадрант)
Функція тангенс як від’ємна функція
Функція тангенса є від’ємною функцією, оскільки тангенс від’ємного кута є від’ємним значенням дотичного додатного кута.
tan (-θ) = – tan θ
Функція тангенса в термінах функції синуса та косинуса
Функцію тангенсу через функції синуса та косинуса можна записати як
tan θ = sin θ/cos θ
Ми знаємо, що tan θ = протилежна сторона/прилегла сторона
Тепер розділіть чисельник і знаменник на гіпотенузу
tan θ = (протилежна сторона/гіпотенуза)/(прилегла сторона/гіпотенуза)
Ми знаємо, що sin θ = протилежна сторона/гіпотенуза
cos θ = прилегла сторона/гіпотенуза
Отже, tan θ = sin θ/cos θ
Функція тангенса в термінах функції синуса
Функцію тангенса в термінах функції синуса можна записати як
tan θ = sin θ/(√1 – sin 2 я)
ми це знаємо,
tan θ = sin θ/cos θ
fizzbuzz java
З тотожностей Піфагора ми маємо,
без2θ + cos2θ = 1
cos2θ = 1 – sin2i
cos θ = √(1 – sin2я)
Отже, tan θ = sin θ/(√1 – sin2я)
Функція тангенса в термінах функції косинуса
Функцію тангенса в термінах функції косинуса можна записати як
tan θ = (√1 -cos 2 i)/cos i
ми це знаємо,
tan θ = sin θ/cos θ
З тотожностей Піфагора ми маємо,
без2θ + cos2θ = 1
без2θ = 1 – cos2i
sin θ = √(1 – cos2я)
Отже, tan θ = (√1 – cos2i)/cos i
Функція тангенс через котангенс
Функцію тангенса в термінах функції котангенса можна записати як
tan θ = 1/cot θ
або
tan θ = cot (90° – θ) (або) cot (π/2 – θ)
Функція тангенс в термінах косекансної функції
Дотичну функцію через косеканс можна записати як
tan θ = 1/√(cosec 2 я – 1)
З тотожностей Піфагора ми маємо,
cosec2θ – ліжечко2θ = 1
ліжечко2θ = cosec2я – 1
cot θ = √(cosec2я – 1)
ми це знаємо,
tan θ = 1/cot θ
Отже, tan θ = 1/√(cosec2я – 1)
Функція дотичної в термінах функції сікуючої
Дотичну функцію через січну можна записати як
tan θ = √сек 2 я – 1
З тотожностей Піфагора ми маємо,
сек2θ – отже2θ = 1
tan θ = сек2я – 1
Отже, tan θ = √(сек2я – 1)
Функція тангенса в термінах подвійного кута
Функція тангенса для подвійного кута:
tan 2θ = (2 tan θ)/(1 – tan 2 я)
Функція тангенса в термінах потрійного кута
Функція тангенса для потрійного кута:
tan 3θ = (3 tan θ – tan 3 θ) / (1 – 3 тан 2 я)
Функція тангенса в термінах півкута
Функція тангенса для півкута:
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / ( sin θ)
Функція тангенса в термінах додавання та віднімання двох кутів
Формули суми та різниці для функції дотичної:
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
tan (A – B) = (tan A – tan B)/(1 + tan A tan B)
Таблиця тригонометричного співвідношення
| Кут (у градусах) | Кут (у радіанах) | гріх я | cos θ | tan θ = sin θ/cos θ | cosec θ | сек θ | ліжечко я |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Невизначено | 1 | Невизначено |
| 30° | стор/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 визначити комп'ютер | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = не визначено | 1 | Невизначено | 0 |
| 120° | 2п/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5п/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | пі | 0 | -1 | 0/(-1) = 0 | Невизначено | -1 | Невизначено |
Розв’язаний приклад дотичних формул
Приклад 1: Знайдіть значення tan θ, якщо sin θ = 2/5 і θ є кутом першого квадранта.
рішення:
враховуючи,
- sin θ = 2/5
З тотожностей Піфагора, які ми маємо,
без2θ + cos2θ = 1
cos2θ = 1 – sin2θ = 1 – (2/5)2
cos2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Оскільки θ є кутом першого квадранта, cos θ додатний.
cos θ = √21/5
ми це знаємо,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
tan θ = 2√21 /21
Отже, значення tan θ, коли sin θ = 2/5 і θ знаходиться в першому квадранті, дорівнює (2√21) /(21)
Приклад 2: Знайдіть значення tan x, якщо sec x = 13/12 і x є кутом четвертого квадранта.
рішення:
Дано, сек х = 13/12
З тотожностей Піфагора ми маємо,
сек2х – отже2х = 1
так2х = сек2x – 1= (13/12)2- 1
так2х = (169/144) – 1= 25/144
tan x = ± 5/12
Оскільки x є кутом четвертого квадранта, tan x є від’ємним.
tan x = – 5/12
Отже, tan x = – 5/12
Приклад 3: якщо tan X = 2/3 і tan Y = 1/2, то яке значення tan (X + Y)?
рішення:
враховуючи,
tan X = 2/3 і tan Y = 1/2
ми це знаємо,
tan (X + Y) = (tan X + tan Y)/(1 – tan X tan Y)
tan (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
Отже, tan(X + Y) = 7/4
Приклад 4. Обчисліть функцію тангенса, якщо прилегла та протилежна сторони прямокутного трикутника дорівнюють 4 см і 7 см відповідно.
рішення:
враховуючи,
Прилегла сторона = 4 см
Протилежна сторона = 7 см
ми це знаємо,
tan θ = протилежна сторона/прилегла сторона
tan θ = 7/4 = 1,75
Отже, tan θ = 1,75
Приклад 5: Людина дивиться на вежу з годинником під кутом 60° до вершини вежі, висота якої 100 м. Яка відстань між людиною та підніжжям вежі?
рішення:
враховуючи,
Висота вежі = 100 м і θ = 60°
Нехай відстань між людиною та підніжжям вежі = d
dateformat.format java
Ми маємо,
tan θ = протилежна сторона/прилегла сторона
tan 60° = 100/д
√3 = 100/d [Оскільки 60° = √3]
d = 100/√3
Отже, відстань між людиною та підніжжям вежі дорівнює 100/√3
Приклад 6: Знайдіть значення tan θ, якщо sin θ = 7/25 і sec θ = 25/24.
рішення:
враховуючи,
sin θ = 7/25
сек θ = 25/24
ми це знаємо,
сек θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Ми маємо,
tan θ = sin θ/cos θ
= (7/25)/(24/25)
= 7/24
Отже, tan θ = 7/24
Приклад 7: Знайдіть значення tan θ, якщо cosec θ = 5/3, а θ є кутом першого квадранта.
рішення:
Дано cosec θ = 5/3
З тотожностей Піфагора ми маємо,
колекції на javacosec2θ – ліжечко2θ = 1
ліжечко2θ = cosec2я – 1
ліжечко θ = (5/3)2– 1 = (25/9) – 1 = 16/9
cot θ = ±√16/9 = ± 4/3
Оскільки θ є кутом першого квадранта, і котангенс, і тангенс є додатними.
ліжечко θ = 4/3
ми це знаємо,
ліжечко θ = 1/tan θ
4/3 = 1/tanθ
tan θ = 3/4
Отже, tan θ = 3/4
Приклад 8: Знайдіть tan 3θ, якщо sin θ = 3/7 і θ є кутом першого квадранта.
рішення:
Дано sin θ = 12/13
З тотожностей Піфагора, які ми маємо,
без2θ + cos2θ = 1
cos2θ = 1 – sin2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Оскільки θ є кутом першого квадранта, cos θ додатний.
cos θ = 5/13
ми це знаємо,
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Отже, tan θ = 12/5
Тепер ми це знаємо,
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
tan 3θ = 3 × (12/5)

