Формули Sin Cos у тригонометрії: Тригонометрія, як випливає з її назви, є наукою про трикутники. Це важлива галузь математики, яка вивчає зв’язок між довжинами сторін і кутами прямокутного трикутника, а також допомагає визначати відсутні довжини сторін або кути трикутника. Існує шість тригонометричних співвідношень або функцій: синус, косинус, тангенс, косеканс, секанс і котангенс, де косеканс, секанс і котангенс є зворотними функціями трьох інших функцій, тобто синуса, косинуса і тангенса відповідно.
Тригонометричне співвідношення визначається як відношення довжин сторін прямокутного трикутника. Тригонометрія використовується в різних сферах нашого повсякденного життя. Це допомагає визначити висоту пагорбів або будівель. Він також використовується в таких галузях, як кримінологія, будівництво, фізика, археологія, морське машинобудування тощо.
У цій статті ми розглянемо все тригонометричні формули, переважно sin і cos формули з їхніми прикладами, а також список усіх формул у тригонометрії.
Зміст
- Формули в тригонометрії
- Деякі основні формули Sin Cos
- Таблиця формул Sin Cos
- Приклади формул Sin Cos
- Практичні завдання на формули Sin Cos у тригонометрії з прикладами
Формули в тригонометрії
Розглянемо прямокутний трикутник XYZ, де ∠Y = 90°. Нехай кут при вершині Z дорівнює θ. Сторона, прилегла до θ, називається прилеглою стороною, а сторона, протилежна θ, називається протилежною стороною. Гіпотенуза - це сторона, протилежна прямому куту, або найдовша сторона прямого кута.
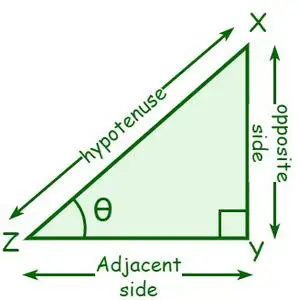
- sin θ = протилежна сторона/гіпотенуза
- cos θ = прилегла сторона/гіпотенуза
- tan θ = протилежна сторона/прилегла сторона
- cosec θ = 1/sin θ = гіпотенуза/протилежна сторона
- сек θ = 1/ cos θ = Гіпотенуза/прилегла сторона
- ліжечко θ = 1/ tan θ = сусідня сторона/протилежна сторона
Формула синуса
Синус кута в прямокутному трикутнику - це відношення довжини протилежної сторони до довжини гіпотенузи до даного кута. Функція синуса представлена як sin.
sin θ = протилежна сторона/гіпотенуза
Формула косинуса
Косинус кута в прямокутному трикутнику - це відношення довжини прилеглої сторони до довжини гіпотенузи до даного кута. Функція косинус представлена як cos.
java переміщення до внутрcos θ = прилегла сторона/гіпотенуза
Деякі основні формули Sin Cos
Функції синус і косинус у квадрантах
- Функція синус додатна в першому і другому квадрантах і від’ємна в третьому і четвертому квадрантах.
- Функція косинуса додатна в першому і четвертому квадрантах і від’ємна в другому і третьому квадрантах.
Ступені
Квадрант
Знак функції синуса
Знак функції косинуса
від 0° до 90°
1-й квадрант
+ (позитивний)
+ (позитивний)
від 90° до 180°
2-й квадрант
+ (позитивний)
– (негативний)
від 180° до 270°
3-й квадрант
– (негативний)
– (негативний)
270° до 360°
4-й квадрант
– (негативний)
+ (позитивний)
Ідентичність негативних кутів функцій синуса та косинуса
- Синус від’ємного кута завжди дорівнює від’ємному синусу кута.
sin (– θ) = – sin θ
- Косинус від’ємного кута завжди дорівнює косинусу кута.
cos (– θ) = cos θ
Співвідношення між функцією синус і косинус
sin θ = cos (90° – θ)
Функції, зворотні функціям синуса і косинуса
- Функція косеканс – це функція, зворотна функції синуса.
cosec θ = 1/sin θ
- Функція секансу є функцією, зворотною функції косинуса.
сек θ = 1/cos θ
Піфагорійська тотожність
без 2 θ + cos 2 θ = 1
Періодичні тотожності функцій синуса і косинуса
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
Формули подвійного кута для функцій синуса та косинуса
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – sin 2 θ = 2 cos 2 θ – 1 = 1 – 2 sin 2 i
Тотожності півкута для функцій синуса та косинуса
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Потрійні кутові тотожності для функцій синуса та косинуса
sin 3θ = 3 sin θ – 4 sin 3 i
cos 3θ = 4cos 3 θ – 3 cos θ
Формули суми та різниці
- Функція синус
sin (A + B) = sin A cos B + cos A sin B
sin (A – B) = sin A cos B – cos A sin B
- Функція косинус
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Закон синусів або правило синусів
Правило синусів — це тригонометричний закон, який визначає співвідношення між довжинами сторін і кутами трикутника.

a/sin A = b/sin B = c/sin C
Де a, b і c — довжини трьох сторін трикутника ABC, а A, B і C — кути.
Закон косинусів
Правило косинусів використовується для визначення відсутніх або невідомих кутів або довжин сторін трикутника.

a 2 = b 2 + c 2 – 2bc cos A
b 2 = c 2 + а 2 – 2ca cos B
в 2 = а 2 + б 2 – 2ab cos C
Де a, b і c — довжини трьох сторін трикутника ABC, а A, B і C — кути.
Таблиця формул Sin Cos
Ось таблиця/список формул Sin і Cos для різних кутів у градусах і радіанах:
Список формул Sin Cos
| Кут (в градусах) | Кут (у радіанах) | гріх я | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | стор/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2п/3 | √3/2 | -1/2 |
| 150° | 5п/6 | 1/2 | -√3/2 |
| 180° | пі | 0 | -1 |
Приклади формул Sin Cos
Задача 1: якщо cos α = 24/25, то знайдіть значення sin α.
рішення:
враховуючи,
cos α = 24/25
З піфагорійських тотожностей ми маємо;
cos2θ + sin2θ = 1
(24/25)2+ без2α = 1
без2α = 1 – (24/25)2
без2α = 1 – (576/625) = (625 – 576)/625
без2α = (625 – 576)/625 = 49/626
sin α = √49/625 = ±7/25
Отже, sin α = ±7/25.
Задача 2: Доведіть формули sin 2A і cos 2A, якщо ∠A= 30°.
рішення:
Дано ∠A= 30°
ми це знаємо,
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Оскільки sin 30° = 1/2, cos 30° = √3/2 і sin 60° = √3/2}
√3/2 = √3/2
L.H.S = П.В.Ш
заблокувати рекламу на youtube android2) cos 2A = 2cos2А – 1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2(√3/2)2– 1 = 3/2 – 1 {Оскільки cos 60° = 1/2 і cos 30° = √3/2}
1/2 = 1/2
L.H.S = П.В.Ш
Звідси доведено.
Задача 3: Знайдіть значення cos x, якщо tan x = 3/4.
рішення:
Дано tan x = 3/4
ми це знаємо,
tan x = протилежна сторона/прилегла сторона = 3/4
Щоб знайти гіпотенузу, скористаємося теоремою Піфагора:
гіпотенуза2= протилежність2+ суміжні2
Х2= 32+ 42
Х2= 9 + 16 = 25
H = √25 = 5
Тепер cos x = сусідня сторона/гіпотенуза
cos x = 4/5
Таким чином, значення cos x дорівнює 4/5.
Задача 4: Знайдіть ∠C (у градусах) і ∠A (у градусах), якщо ∠B = 45°, BC = 15 дюймів і AC = 12 дюймів.

рішення:
Дано: ∠B = 45°, BC = a = 15 дюймів і AC = b = 12 дюймів.
З закону синусів ми маємо
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ без А = 15/16,97 = 0,8839
⇒ ∠A = sin-1(0,8839) = 62,11°
Ми знаємо, що сума внутрішніх кутів трикутника дорівнює 180°.
Отже, ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Отже, ∠A = 62,11° і ∠C = 72,89°.
Задача 5: Доведіть тотожності півкута функції косинус.
рішення:
Тотожність півкута функції косинуса дорівнює:
cos (θ/2) = ±√[(1 + cos θ)/2]
З подвійних кутових тотожностей ми маємо,
cos 2A = 2 cos2А – 1
Тепер замініть A на θ/2 з обох сторін
⇒ cos 2(θ/2) = 2 cos2(і/2) – 1
⇒ cos θ = 2 cos2(і/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ cos2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Звідси доведено.
Практичні завдання на формули Sin Cos у тригонометрії з прикладами
1. Дано sin θ = 3/5. Знайти cos θ.
2. Доведіть тотожність sin(2A) = 2 sinA cosA для A=45∘.
3. Якщо cos α = 5/13. Знайдіть sin(2a).
4. Визначте θ, якщо sin θ = cos(90∘−θ).
5. Якщо tan β = 2. Знайдіть sin β і cos β, використовуючи тотожність Піфагора.
Поширені запитання щодо формул Sin Cos у тригонометрії з прикладами
Які основні формули синусів і косинусів тригонометрії?
Основні формули синуса та косинуса: sin θ = протилежна/гіпотенуза та cos θ = прилегла/гіпотенуза, де θ — кут у прямокутному трикутнику.
Як знайти синус і косинус особливих кутів?
Спеціальні кути, такі як 0∘, 30∘, 45∘, 60∘ та 90∘, мають конкретні значення синуса та косинуса, які можна запам’ятати за допомогою тригонометричних таблиць або концепцій одиничного кола.
Який зв’язок між функціями синус і косинус?
Функції синус і косинус пов’язані одиницею sin θ = cos(90∘- θ) і тотожність Піфагора без 2 θ+cos 2 θ = 1.
Як ви використовуєте формули подвійного кута для синуса та косинуса?
Формули подвійного кута є sin(2θ) = 2sinθcosθ і cos(2θ)=cos 2 θ – sin 2 i. Вони використовуються для вираження тригонометричних функцій подвійних кутів через одиничні кути.
Як знайти значення синуса та косинуса для кутів у різних квадрантах?
Знаки функцій синуса і косинуса залежать від того, в якому квадранті лежить кут:
- Перший квадрант: sin θ> 0 і cos θ> 0
- Другий квадрант: sin θ> 0 і cos θ <0
- Третій квадрант: sinθ <0 і cosθ < 0
- Четвертий квадрант: sinθ 0
