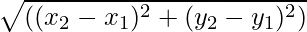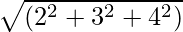ВЕЛИЧИНА ВЕКТОРА - ВИЗНАЧЕННЯ, ФОРМУЛА, ПРИКЛАДИ ТА ПОШИРЕНІ ЗАПИТАННЯ

Векторні величини — це величини, які мають як напрямок, так і величину. Величина вектора - це довжина вектора. Він задається числовим значенням вектора, і оскільки він представляє довжину вектора, тому він завжди додатний. Для будь-якого вектора 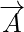overrightarrow{A} його величина представлена як .

Давайте дізнаємося більше про величину вектора, його формулу, приклади та інше в цій статті.

Зміст

Що таке величина вектора?
Величина векторної формули
Напрямок вектора
Як знайти величину вектора?
Розв'язані приклади

Що таке величина вектора?

Величина вектора визначається як довжина вектора. Оскільки величина вектора означає довжину вектора, вона завжди додатна. Для будь-якого вектора A його величина представлена як |A|. Припустимо, що вектор визначається як xi + yj, тоді його величина визначається як квадратний корінь із суми квадратів окремих членів. Величина вектора представляє довжину вектора, тобто значення або вплив, який має вектор.

Наприклад, якщо на об’єкт діє сила 5i Н, то її величина дорівнює 5 Н, що означає, що сила прикладеної сили становить 5 Н, і « я у 5i означає, що він застосований у додатному напрямку x.

Величина векторної формули

Існують різні способи обчислення величини вектора. На основі наведених даних скористайтеся іншою формулою, щоб знайти величину вектора. Величина вектора A представлена за допомогою оператора модуля, тобто |A|

Існують різні формули, які використовуються для підрахунку величини вектора. На наступному зображенні показано важливі формули, які використовуються для визначення величини вектора.

Нижче наведено способи обчислення величини.

Якщо їм задано вектор Ā = xi+ yĵ + zk̂, то величину вектора Ā можна обчислити за наведеною нижче формулою

Величина вектора Ā (|A|) = √(x ² + і ² +z ² )

Якщо вектор початкової точки, скажімо, (x₁, і₁), а кінцевою точкою вектора є, скажімо, (x₂, і₂) задано величину вектора надається,

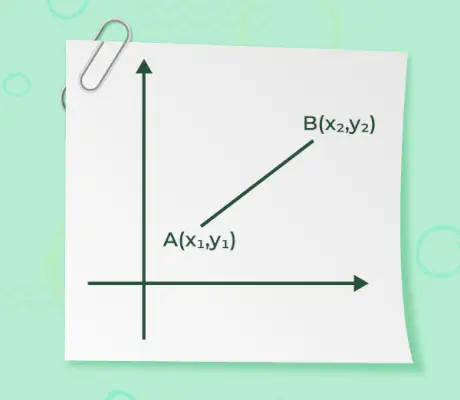
Величина вектора, коли дано початкову та кінцеву точки вектора, є не що інше, як відстань між точками. Формула для знаходження величини дається за формулою

= $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

Якщо будь-яка початкова або кінцева точка вектора знаходиться в точці координат o(0, 0), а інша точка знаходиться A(x, y) як показано на малюнку нижче,

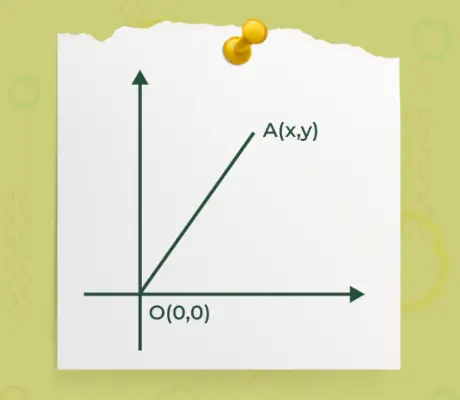
Величина вектора, якщо задано одну точку та початок координат

Тоді формула для знаходження величини вектора, де один із кінців вектора знаходиться в початку координат, має вигляд

|Ā| = √(x ² +y ² )

Напрямок вектора

Векторні величини — це величини, які мають як величину, так і напрямок. Напрямок векторної величини означає, у якому напрямку векторна величина застосована. Він визначається як кут, який вектор утворює з горизонтальною лінією або віссю x. Він представлений символом a .

На зображенні нижче показано стрілку, яка використовується для показу напрямку вектора.

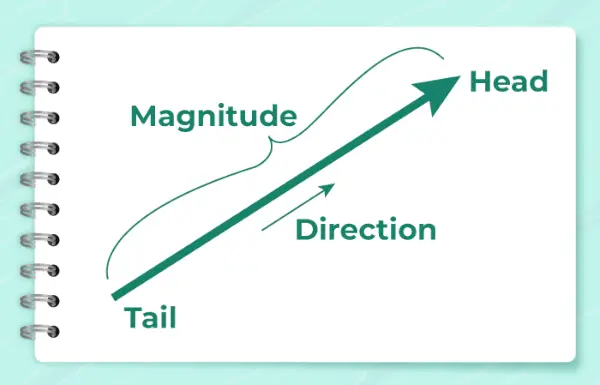
Розраховується за формулою,

α = загар ^-1 (y/x)
масив сортування в java

Для вектора, породженого координатами (x₁, і₁) і (x₂, і₂) їх напрямок задається формулою,

α = загар ^-1 [(і ₂ - і ₁ )/(x ₂ – х ₁ )]

Як знайти величину вектора?

Величина вектора обчислюється за допомогою кроків, описаних нижче,

Крок 1: Визначте компоненти x, y та z вектора.

Крок 2 : Знайдіть квадрат усіх компонентів x, y та z.

крок 3: Додайте всі квадрати, знайдені на кроці 2.

крок 4: Знайдіть квадратний корінь із суми, отриманої на кроці 3.

Значення, отримане після кроку 4, є величиною даного вектора.

Приклад: Знайдіть величину вектора A = 3i + 4j

рішення:

Величина вектора A обчислюється за допомогою описаних вище кроків.

Крок 1: Порівнюючи A = 3i + 4j з xi + yj, ми отримуємо x = 3 і y = 4

крок 2: x²= 3²= 9 і y²= 4²= 16

крок 3: x²+ і²= 9 + 16 = 25

крок 4: √(25) = 5

Таким чином, величина вектора A = 3i + 4j дорівнює 5 одиницям.

Висновок

Підсумовуючи, величина вектора говорить нам про довжину вектора. Ця концепція дуже важлива в багатьох галузях, таких як фізика, техніка та інформатика, оскільки вона допомагає вимірювати такі речі, як швидкість, сила та напрямок руху. Розуміючи векторну величину, ми можемо краще аналізувати та розв’язувати практичні проблеми, роблячи її ключовим знанням для тих, хто працює з числами та вимірюваннями в реальних програмах.

які розміри екрана мого комп’ютера

Детальніше,

Скаляр і вектор
Векторні операції
Як обчислити одиничний вектор?

Розв'язані приклади на величину вектора

Приклад 1: Знайдіть величину для вектора Ā = 2i + 3ĵ + 4k.

рішення:

випадковий відсутність генератора в java

враховуючи,

Ā = 2i + 3ĵ + 4k

Величина |A| = $sqrt{(2^2+3^2+4^2)}$

=
= √29
= 5,38

Величина вектора 2i+3ĵ+4k є 5.38 одиниця

Приклад 2: Знайти величину для вектора Ā = 3i + 3ĵ – 6k

рішення:

Дано

Ā = 3i + 3ĵ – 6k

Величина |A| = $sqrt{(3^2+3^2+(-6)^2)}$

=
= √54
= 7,35

Величина вектора 3i+ 3ĵ – 6k є 7.35 одиниця.

Приклад 3: Знайти величину вектора, якщо початкова точка вектора дорівнює (3, 4), а кінцева точка — (6, 2).

рішення:

враховуючи,

(х₁, і₁) = (3, 4)
(х₂, і₂) = (6, 2)

|Ā|= $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

= $sqrt{((6-3)^2+(2-4)^2)}$
= √(3²+ (-2)²)
= √(9+4)
= √13 = 3,6

Таким чином, величина заданого вектора становить 3.6 одиниця.

Приклад 4. Знайдіть величину вектора, якщо початкова точка вектора дорівнює (2, 1, 4), а кінцева — (5, 2, 6).

рішення:

враховуючи,
алгебра множин

(х₁, і₁, С₁) = (2, 1, 4)

(х₂, і₂, С₂) = (5, 2, 6)

|Ā| = $sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}$

= $sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}$
=
= √(9 +1 + 4)
= √14 = 3,74

Таким чином, величина заданого вектора становить 3.74 одиниця.

Приклад 5: яка величина вектора, який починається з початку координат і закінчується в (3, 4).

рішення:

враховуючи,

Початкова точка вектора - O(0, 0)

Кінцева точка (x, y) = (3, 4)

Величина вектора (|Ā|) = √(x²+y²)

= √(3²+ 4²)
= √(9 + 16)
= √25 = 5

Таким чином, величина заданого вектора становить 5 одиниця.

Приклад 6: Знайти величину вектора, у якому одна з кінцевих точок знаходиться в початку координат, а інша точка в (1, 4, 3).

рішення:

враховуючи,

Кінцева точка вектора – O(0, 0)

Інша точка (x, y, z) = (1, 4, 3)

Величина вектора (|Ā|) = √(x²+y²+z²)

= $sqrt{(1^2+4^2+3^2)}$
=
= √26 = 5,09

Таким чином, величина заданого вектора становить 5.09 одиниця.
жирний шрифт в css

Поширені запитання щодо величини вектора

Що таке величина векторної формули?

Величина вектора — це числове значення вектора, яке визначає довжину вектора. Для будь-якого вектора A його величина представлена як |A|. Величина вектора обчислюється за формулою

Для будь-якого вектора A = xi + yj + zk його величина визначається формулою

|A| = √(x ² + і ² + z ² )

Для будь-якого вектора, початкова та кінцева точки якого дорівнюють відповідно (x₁, і₁) і (x₂, і₂) його величина визначається формулою

|A| = √((x ₂ – х ₁ ) ² + (і ₂ - і ₁ ) ² )

Як представити величину вектора?

Величина вектора А позначається символом |A|.

Як знайти величину вектора?

Для обчислення величини вектора використовуються різні формули, деякі з них:

|A| = √(x ² + і ² + z ² ) коли вектор має форму A = xi + yj + zk
|A| = √((x) ² + (та) ² ) коли вектор задано точкою A (x, y) і початком координат O(0, 0).
|A| = √((x ₂ – х ₁ ) ² + (і ₂ - і ₁ ) ² ) коли вектор задано точкою A (x₁, і₂) і точка B (x₂, і₂).

Знайдіть вектор величини 5.

Існують різні вектори, які можуть мати величину 5, прикладом яких є вектор A, представлений у вигляді

A = 3i + 4j Або A = 4i + 5j