Логістична регресія це контрольований алгоритм машинного навчання використовуваний для класифікаційні завдання де метою є передбачити ймовірність того, що примірник належить до даного класу чи ні. Логістична регресія – це статистичний алгоритм, який аналізує зв’язок між двома факторами даних. У статті досліджуються основи логістичної регресії, її види та реалізації.

Зміст

• Що таке логістична регресія?
• Логістична функція – сигмоїдна функція
• Типи логістичної регресії
• Припущення логістичної регресії
• Як працює логістична регресія?
• Реалізація коду для логістичної регресії
• Компроміс Precision-Recall у встановленні порогу логістичної регресії
• Як оцінити модель логістичної регресії?
• Відмінності між лінійною та логістичною регресією

Що таке логістична регресія?

Логістична регресія використовується для двійкових класифікація де ми використовуємо сигмовидна функція , який приймає вхідні дані як незалежні змінні та створює значення ймовірності від 0 до 1.

Наприклад, ми маємо два класи: клас 0 і клас 1, якщо значення логістичної функції для вхідних даних перевищує 0,5 (порогове значення), тоді воно належить до класу 1, інакше воно належить до класу 0. Це називається регресією, оскільки воно є розширенням лінійна регресія але в основному використовується для проблем класифікації.

Ключові моменти:

• Логістична регресія передбачає вихід категоріальної залежної змінної. Отже, результат повинен мати категоричне або дискретне значення.
• Це може бути «Так» або «Ні», «0» або «1», «Істинно» або «Хибно» тощо, але замість того, щоб давати точне значення як 0 і 1, воно дає ймовірнісні значення, які знаходяться між 0 і 1.
• У логістичній регресії замість підгонки лінії регресії ми підбираємо S-подібну логістичну функцію, яка передбачає два максимальні значення (0 або 1).

Логістична функція – сигмоїдна функція

• Сигмоїдна функція – це математична функція, яка використовується для відображення прогнозованих значень у ймовірності.
• Він перетворює будь-яке реальне значення на інше значення в діапазоні від 0 до 1. Значення логістичної регресії має бути між 0 і 1, яке не може виходити за межі цієї межі, тому воно утворює криву, подібну до форми S.
• Крива S-форми називається сигмоїдною функцією або логістичною функцією.
• У логістичній регресії ми використовуємо поняття порогового значення, яке визначає ймовірність 0 або 1. Наприклад, значення вище порогового значення прагне до 1, а значення нижче порогових значень прагне до 0.

Типи логістичної регресії

На основі категорій логістичну регресію можна класифікувати на три типи:

1. біном: У біноміальній логістичній регресії може бути лише два можливих типи залежних змінних, наприклад 0 або 1, «Здано» або «Не пройдено» тощо.
2. Багаточлен: У мультиноміальній логістичній регресії може бути 3 або більше можливих невпорядкованих типів залежної змінної, наприклад кішка, собака або вівця.
3. Порядковий номер: У порядковій логістичній регресії може бути 3 або більше можливих упорядкованих типів залежних змінних, наприклад низький, середній або високий.

Припущення логістичної регресії

Ми досліджуватимемо припущення логістичної регресії, оскільки розуміння цих припущень є важливим для того, щоб переконатися, що ми використовуємо належне застосування моделі. Припущення включає:

1. Незалежні спостереження: кожне спостереження не залежить від іншого. тобто немає кореляції між будь-якими вхідними змінними.
2. Двійкові залежні змінні: передбачається, що залежна змінна має бути двійковою або дихотомічною, тобто вона може приймати лише два значення. Для більш ніж двох категорій використовуються функції SoftMax.
3. Лінійний зв’язок між незалежними змінними та логарифмом шансів: зв’язок між незалежними змінними та логарифмом шансів залежної змінної має бути лінійним.
4. Без викидів: у наборі даних не повинно бути викидів.
5. Великий розмір вибірки: розмір вибірки достатньо великий

Термінології, залучені до логістичної регресії

Ось деякі загальні терміни, що застосовуються до логістичної регресії:

• Незалежні змінні: Вхідні характеристики або фактори прогнозу, застосовані до прогнозів залежної змінної.
• Залежна змінна: Цільова змінна в моделі логістичної регресії, яку ми намагаємося передбачити.
• Логістична функція: Формула, яка використовується для представлення того, як незалежні та залежні змінні співвідносяться одна з одною. Логістична функція перетворює вхідні змінні в значення ймовірності між 0 і 1, яке представляє ймовірність того, що залежна змінна дорівнює 1 або 0.
• Шанси: Це відношення того, що відбувається, до того, що не відбувається. вона відрізняється від ймовірності, оскільки ймовірність є відношенням того, що щось станеться, до всього, що може статися.
• Логічні коефіцієнти: Логарифм шансів, також відомий як функція логіт, є натуральним логарифмом шансів. У логістичній регресії логарифм шансів залежної змінної моделюється як лінійна комбінація незалежних змінних і відрізка.
• Коефіцієнт: Розраховані параметри моделі логістичної регресії показують, як незалежні та залежні змінні співвідносяться одна з одною.
• Перехоплення: Постійний член у моделі логістичної регресії, який представляє логарифм шансів, коли всі незалежні змінні дорівнюють нулю.
• Оцінка максимальної правдоподібності : Метод, що використовується для оцінки коефіцієнтів моделі логістичної регресії, який максимізує ймовірність спостереження за даними моделі.

Як працює логістична регресія?

Модель логістичної регресії перетворює лінійна регресія Функція безперервного виведення значення у вихід категоріального значення за допомогою сигмоїдної функції, яка відображає будь-який дійсний набір незалежних змінних, введених у значення від 0 до 1. Ця функція відома як логістична функція.

Нехай незалежні вхідні характеристики:

X = egin{bmatrix} x_{11} & … & x_{1m} x_{21} & … & x_{2m} vdots & ddots & vdots x_{n1} & … & x_{nm} end{bmatrix}

а залежною змінною є Y, що має лише двійкове значення, тобто 0 або 1.

типи даних java

Y = egin{cases} 0 & ext{ if } Class;1 1 & ext{ if } Class;2 end{cases}

потім застосуйте багатолінійну функцію до вхідних змінних X.

z = left(sum_{i=1}^{n} w_{i}x_{i} ight) + b

тутx_i є i-м спостереженням X,w_i = [w_1, w_2, w_3, cdots,w_m] це вагові коефіцієнти або коефіцієнт, а b є зміщенням, також відомим як перехоплення. просто це можна представити як скалярний добуток ваги та зміщення.

z = wcdot X +b

те, що ми обговорювали вище, є лінійна регресія .

Сигмоїдна функція

Тепер ми використовуємо сигмовидна функція де введенням буде z, і ми знаходимо ймовірність між 0 і 1, тобто передбачуваним y.

sigma(z) = frac{1}{1-e^{-z}}

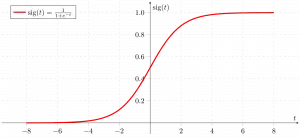
Сигмоподібна функція

Як показано вище, сигмоїдна функція фігури перетворює дані безперервної змінної в ймовірність тобто між 0 і 1.

• sigma(z) прагне до 1 асz ightarrowinfty
• sigma(z) прагне до 0 якz ightarrow-infty
• sigma(z) завжди обмежена між 0 і 1

де ймовірність бути класом можна виміряти як:

P(y=1) = sigma(z) P(y=0) = 1-sigma(z)

Рівняння логістичної регресії

Непарність — це відношення того, що відбувається, до того, що не відбувається. вона відрізняється від ймовірності, оскільки ймовірність є відношенням того, що щось станеться, до всього, що може статися. так дивно буде:

frac{p(x)}{1-p(x)} = e^z

Застосування натурального журналу до непарних. тоді log odd буде:

egin{aligned} log left[frac{p(x)}{1-p(x)} ight] &= z log left[frac{p(x)}{1-p(x)} ight] &= wcdot X +b frac{p(x)}{1-p(x)}&= e^{wcdot X +b} ;;cdots ext{Exponentiate both sides} p(x) &=e^{wcdot X +b}cdot (1-p(x)) p(x) &=e^{wcdot X +b}-e^{wcdot X +b}cdot p(x)) p(x)+e^{wcdot X +b}cdot p(x))&=e^{wcdot X +b} p(x)(1+e^{wcdot X +b}) &=e^{wcdot X +b} p(x)&= frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} end{aligned}

тоді кінцеве рівняння логістичної регресії буде таким:

p(X;b,w) = frac{e^{wcdot X +b}}{1+e^{wcdot X +b}} = frac{1}{1+e^{-wcdot X +b}}

Функція правдоподібності для логістичної регресії

Передбачувані ймовірності будуть:

• для y=1 Прогнозована ймовірність буде: p(X;b,w) = p(x)
• для y = 0 Прогнозовані ймовірності будуть такими: 1-p(X;b,w) = 1-p(x)

L(b,w) = prod_{i=1}^{n}p(x_i)^{y_i}(1-p(x_i))^{1-y_i}

Взяття натуральних колод з обох сторін

egin{aligned}log(L(b,w)) &= sum_{i=1}^{n} y_ilog p(x_i);+; (1-y_i)log(1-p(x_i)) &=sum_{i=1}^{n} y_ilog p(x_i)+log(1-p(x_i))-y_ilog(1-p(x_i)) &=sum_{i=1}^{n} log(1-p(x_i)) +sum_{i=1}^{n}y_ilog frac{p(x_i)}{1-p(x_i} &=sum_{i=1}^{n} -log1-e^{-(wcdot x_i+b)} +sum_{i=1}^{n}y_i (wcdot x_i +b) &=sum_{i=1}^{n} -log1+e^{wcdot x_i+b} +sum_{i=1}^{n}y_i (wcdot x_i +b) end{aligned}

Градієнт логарифмічної функції правдоподібності

Щоб знайти оцінки максимальної ймовірності, ми диференціюємо w.r.t w,

egin{aligned} frac{partial J(l(b,w)}{partial w_j}&=-sum_{i=n}^{n}frac{1}{1+e^{wcdot x_i+b}}e^{wcdot x_i+b} x_{ij} +sum_{i=1}^{n}y_{i}x_{ij} &=-sum_{i=n}^{n}p(x_i;b,w)x_{ij}+sum_{i=1}^{n}y_{i}x_{ij} &=sum_{i=n}^{n}(y_i -p(x_i;b,w))x_{ij} end{aligned}

Реалізація коду для логістичної регресії

Біноміальна логістична регресія:

Цільова змінна може мати лише 2 можливі типи: 0 або 1, які можуть представляти перемогу чи поразку, успішність чи невдачу, мертву чи живу тощо, у цьому випадку використовуються сигмоїдні функції, які вже обговорювалися вище.

перевизначення методу в java

Імпорт необхідних бібліотек на основі вимог моделі. Цей код Python показує, як використовувати набір даних про рак молочної залози для реалізації моделі логістичної регресії для класифікації.

Вихід :

Точність моделі логістичної регресії (у %): 95,6140350877193

де налаштування браузера

Мультиноміальна логістична регресія:

Цільова змінна може мати 3 або більше можливих типів, які не впорядковані (тобто типи не мають кількісної значущості), як-от хвороба A проти хвороби B проти хвороби C.

У цьому випадку функція softmax використовується замість сигмоїдної функції. Функція Softmax для K класів буде:

ext{softmax}(z_i) =frac{ e^{z_i}}{sum_{j=1}^{K}e^{z_{j}}}

тут, К представляє кількість елементів у векторі z, а i, j повторює всі елементи у векторі.

Тоді ймовірність для класу c буде:

P(Y=c | overrightarrow{X}=x) = frac{e^{w_c cdot x + b_c}}{sum_{k=1}^{K}e^{w_k cdot x + b_k}}

У мультиноміальній логістичній регресії вихідна змінна може мати більше двох можливих дискретних виходів . Розглянемо набір даних Digit.

Вихід:

Точність моделі логістичної регресії (у %): 96,52294853963839

Як оцінити модель логістичної регресії?

Ми можемо оцінити модель логістичної регресії за допомогою таких показників:

• Точність: Точність надає частку правильно класифікованих екземплярів.
  Accuracy = frac{True , Positives + True , Negatives}{Total}

• Точність: Точність акцентує увагу на точності позитивних прогнозів.
  Precision = frac{True , Positives }{True, Positives + False , Positives}

• Запам'ятовування (чутливість або істинно позитивний рівень): Відкликати вимірює частку правильно передбачених позитивних випадків серед усіх фактичних позитивних випадків.
  Recall = frac{ True , Positives}{True, Positives + False , Negatives}

• Оцінка F1: Оцінка F1 це середнє гармонічне точності та відкликання.
  F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}

• Площа під кривою робочих характеристик приймача (AUC-ROC): Крива ROC відображає істинний позитивний рівень проти помилкового позитивного показника за різних порогових значень. АМУ-РПЦ вимірює площу під цією кривою, забезпечуючи сукупний показник ефективності моделі за різними пороговими значеннями класифікації.
• Площа під кривою точності запам'ятовування (AUC-PR): Подібно до AUC-ROC, AUC-PR вимірює площу під кривою точності запам’ятовування, надаючи короткий підсумок продуктивності моделі за різними компромісами точності запам’ятовування.

Компроміс Precision-Recall у встановленні порогу логістичної регресії

Логістична регресія стає методом класифікації лише тоді, коли в картину вводиться поріг прийняття рішення. Встановлення порогового значення є дуже важливим аспектом логістичної регресії та залежить від самої проблеми класифікації.

На рішення щодо значення порогового значення значною мірою впливають значення точність і відкликання. В ідеалі ми хочемо, щоб і точність, і запам’ятовування дорівнювали 1, але це буває рідко.

У випадку а Компроміс Precision-Recall , ми використовуємо такі аргументи, щоб визначити порогове значення:

1. Низька точність/високе запам'ятовування: У програмах, де ми хочемо зменшити кількість хибних негативів без обов’язкового зменшення кількості помилкових спрацьовувань, ми вибираємо значення рішення, яке має низьке значення Precision або високе значення Recall. Наприклад, у програмі діагностики раку ми не хочемо, щоб будь-який уражений пацієнт класифікувався як неуражений, не приділяючи особливої ​​уваги тому, якщо пацієнту помилково діагностовано рак. Це пов’язано з тим, що відсутність раку можна виявити за подальшими медичними захворюваннями, але наявність захворювання не можна виявити у вже відхиленого кандидата.
2. Висока точність/низьке запам'ятовування: У програмах, де ми хочемо зменшити кількість помилкових спрацьовувань без обов’язкового зменшення кількості помилкових негативів, ми вибираємо значення рішення, яке має високе значення Precision або низьке значення Recall. Наприклад, якщо ми класифікуємо клієнтів, позитивно чи негативно вони відреагують на персоналізовану рекламу, ми хочемо бути абсолютно впевнені, що клієнт відреагує на рекламу позитивно, оскільки в іншому випадку негативна реакція може спричинити втрату потенційних продажів від клієнт.

Відмінності між лінійною та логістичною регресією

Різниця між лінійною регресією та логістичною регресією полягає в тому, що результат лінійної регресії є безперервним значенням, яке може бути будь-яким, тоді як логістична регресія передбачає ймовірність того, що примірник належить до певного класу чи ні.

Логістична регресія – поширені запитання (FAQ)

Що таке логістична регресія в машинному навчанні?

Логістична регресія — це статистичний метод розробки моделей машинного навчання з двійковими залежними змінними, тобто двійковими. Логістична регресія — це статистичний метод, який використовується для опису даних і зв’язку між однією залежною змінною та однією або кількома незалежними змінними.

Які є три типи логістичної регресії?

Логістичну регресію поділяють на три типи: бінарну, багаточленну та порядкову. Вони відрізняються як виконанням, так і теорією. Бінарна регресія розглядає два можливі результати: так чи ні. Мультиноміальна логістична регресія використовується, коли є три або більше значень.

Чому для задачі класифікації використовується логістична регресія?

Логістичну регресію легше реалізувати, інтерпретувати та навчати. Він дуже швидко класифікує невідомі записи. Коли набір даних є лінійно роздільним, він працює добре. Коефіцієнти моделі можна інтерпретувати як показники важливості ознак.

Що відрізняє логістичну регресію від лінійної?

У той час як лінійна регресія використовується для прогнозування безперервних результатів, логістична регресія використовується для прогнозування ймовірності потрапляння спостереження в конкретну категорію. Логістична регресія використовує S-подібну логістичну функцію для відображення прогнозованих значень від 0 до 1.

Яку роль відіграє логістична функція в логістичній регресії?

Логістична регресія покладається на логістичну функцію для перетворення результату в оцінку ймовірності. Ця оцінка представляє ймовірність того, що спостереження належить до певного класу. S-подібна крива допомагає визначити порогові значення та класифікувати дані в двійкові результати.