Лінійне програмування це математичне поняття, яке використовується для знаходження оптимального розв’язку лінійної функції. Цей метод використовує прості припущення для оптимізації заданої функції. Лінійне програмування має величезне застосування в реальному світі та використовується для вирішення різних типів задач.
Лінійне програмування використовується в різних галузях, таких як судноплавство, обробна промисловість, транспорт, телекомунікації та інші.
Термін «лінійне програмування» складається з двох слів «лінійний» і «програмування». Слово «лінійне» вказує на зв’язок між різними типами змінних першого ступеня, які використовуються в задачі, а слово «програмування» вказує нам покрокову процедуру вирішення цих проблем.
У цій статті ми детально дізнаємося про лінійне програмування, його приклади, формули та інші поняття.
Зміст
- Що таке лінійне програмування?
- Компоненти лінійного програмування
- Приклади лінійного програмування
- Задачі лінійного програмування
- Типи задач лінійного програмування
- Формула лінійного програмування
- Як розв’язувати задачі лінійного програмування?
- Методи лінійного програмування
- Симплексний метод лінійного програмування
- Графічний метод лінійного програмування
- Програми лінійного програмування
- Важливість лінійного програмування
- Сучасні програми лінійного програмування
- Лінійне програмування в дослідженні операцій
- Симплексний метод
Що таке лінійне програмування?
Лінійне програмування або Лінійна оптимізація це техніка, яка допомагає нам знайти оптимальне рішення для даної проблеми, оптимальне рішення – це рішення, яке є найкращим можливим результатом даної конкретної проблеми.
Простіше кажучи, це спосіб дізнатися, як зробити щось найкращим способом. З обмеженими ресурсами вам потрібно оптимально використовувати ресурси та досягати найкращого можливого результату в конкретній меті, наприклад найменших витрат, найвищої маржі або найменшого часу.
Ситуація, яка вимагає пошуку найкращих значень змінних з певними обмеженнями, полягає в тому, що ми використовуємо задачі лінійного програмування. Ці ситуації неможливо вирішити за допомогою звичайних обчислень і чисельних методів.
Визначення лінійного програмування
Лінійне програмування — це техніка, яка використовується для оптимізації конкретного сценарію. Використання лінійного програмування дає нам найкращий можливий результат у певній ситуації. Він використовує всі доступні ресурси таким чином, щоб отримати оптимальний результат.
Компоненти лінійного програмування
Основними компонентами задачі лінійного програмування (LP) є:
- Змінні рішення: Змінні, які потрібно визначити для досягнення оптимального рішення.
- Цільова функція: М атематичне рівняння, яке представляє мету, яку ви хочете досягти
- Обмеження: Обмеження чи обмеження, яким мають відповідати ваші змінні рішення.
- Обмеження без негативу: В деяких сценаріїв реального світу, змінні рішення не можуть бути негативними
Додаткові характеристики лінійного програмування
- Скінченність: Кількість змінних рішення та обмежень у задачі ЛП є кінцевою.
- Лінійність: Цільова функція та всі обмеження мають бути лінійними функціями змінних рішення . Це означає, що ступінь змінних має бути один.
Приклади лінійного програмування
Ми можемо зрозуміти ситуації, в яких застосовується лінійне програмування, за допомогою прикладу, розглянутого нижче,
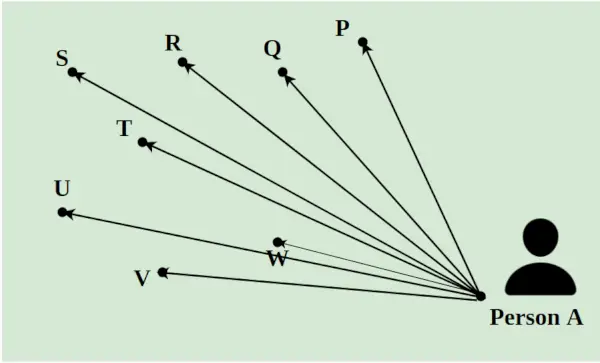
Припустімо, що кур’єр повинен доставити 8 пакетів на день у різні куточки міста. Він повинен вибрати всі пакети з A і доставити їх до точок P, Q, R, S, T, U, V і W. Відстань між ними вказана за допомогою ліній, як показано на зображенні нижче. Найкоротший шлях, яким слідує кур’єр, розраховується за допомогою концепції лінійного програмування.
пекло зворотного виклику в javascript
Задачі лінійного програмування
Задачі лінійного програмування (LPP) включають оптимізацію лінійної функції, щоб знайти оптимальне значення для функції. Оптимальним значенням може бути як максимальне значення, так і мінімальне значення.
У LPP лінійні функції називаються цільові функції. Цільова функція може мати кілька змінних, які підпорядковуються умовам і повинні задовольняти лінійні обмеження .
Типи задач лінійного програмування
Існує багато різних задач лінійного програмування (LPP), але в цій статті ми розглянемо три основні проблеми лінійного програмування.
Виробничі проблеми
Виробничі проблеми — це проблема, яка пов’язана з кількістю одиниць, які слід виробити або продати, щоб максимізувати прибуток, коли кожен продукт вимагає фіксованої робочої сили, машино-годин і сировини.
Проблеми з дієтою
Він використовується для розрахунку кількості різних видів інгредієнтів, які необхідно включити в раціон, щоб отримати мінімальну вартість, залежно від наявності продуктів і їх цін.
Транспортні проблеми
Він використовується для визначення розкладу транспортування, щоб знайти найдешевший спосіб транспортування продукту з заводів/фабрик, розташованих у різних місцях, на різні ринки.
Формула лінійного програмування
Задача лінійного програмування складається з
- Змінні рішення
- Цільова функція
- обмеження
- Невід’ємні обмеження
Змінні рішення це змінні x і y, які визначають результат задачі лінійного програмування та представляють остаточне рішення.
The цільова функція , як правило, представлений Z, є лінійною функцією, яку необхідно оптимізувати відповідно до заданої умови, щоб отримати остаточне рішення.
The обмеження накладені на змінні рішення, які обмежують їх значення, називаються обмеженнями.
Тепер загальна формула задачі лінійного програмування така:
Цільова функція : Z = ax + by
Обмеження: cx + dy ≥ e, px + qy ≤ r
Невід’ємні обмеження: x ≥ 0, y ≥ 0
У наведеній вище умові x і y є змінними рішення.
Як розв’язувати задачі лінійного програмування?
Перш ніж розв'язувати задачі лінійного програмування, спочатку ми повинні сформулювати задачі відповідно до стандартних параметрів. Кроки розв’язування задач лінійного програмування:
Крок 1: Позначте в задачі змінні рішення.
Крок 2: Побудуйте цільову функцію задачі та перевірте, чи потрібно цю функцію мінімізувати чи максимізувати.
крок 3: Запишіть усі обмеження лінійних задач.
крок 4: Забезпечити невід’ємні обмеження змінних рішення.
крок 5: Тепер розв’яжіть задачу лінійного програмування будь-яким методом, зазвичай ми використовуємо або симплексний, або графічний метод.
Методи лінійного програмування
Ми використовуємо різні методи розв'язування задач лінійного програмування. Два найпоширеніших методу:
- Симплексний метод
- Графічний метод
Давайте детально дізнаємося про ці два методи в цій статті,
Симплексний метод лінійного програмування
Одним із найпоширеніших методів вирішення задач лінійного програмування є симплекс-метод. У цьому методі ми повторюємо певну умову «n» кілька разів, доки не буде досягнуто оптимальне рішення.
Кроки, необхідні для вирішення задач лінійного програмування за допомогою симплекс-методу:
Крок 1: Сформулювати задачі лінійного програмування на основі заданих обмежень.
Крок 2: Перетворіть усі задані нерівності на рівняння або рівності задач лінійного програмування, додавши змінну slack до кожної нерівності, де це необхідно.
крок 3: Побудуйте вихідну симплексну таблицю. Представляючи кожне рівняння обмежень у рядку та записуючи цільову функцію в нижньому рядку. Отриману таким чином таблицю називають симплексною таблицею.
крок 4: Визначте найбільший негативний запис у нижньому рядку, стовпець елемента з найбільшим негативним записом називається опорним стовпцем
крок 5: Розділіть записи крайнього правого стовпця з записами відповідного зведеного стовпця, за винятком записів самого нижнього рядка. Тепер рядок, що містить найменший запис, називається опорним. Поворотний елемент виходить перетином опорного рядка і опорного стовпця.
крок 6: Використовуючи матричну операцію та за допомогою елемента зведення, зробіть усі записи у стовпці зведення нульовими.
Крок 7: Перевірте наявність невід’ємних записів у самому нижньому рядку, якщо в нижньому рядку немає негативних записів, завершіть процес, інакше почніть процес знову з кроку 4.
Крок 8: Остаточна симплексна таблиця, отримана таким чином, дає розв’язок нашої проблеми.
Графічний метод лінійного програмування
Графічний метод є іншим методом, ніж симплексний метод, який використовується для вирішення задач лінійного програмування. Як випливає з назви, цей метод використовує графіки для розв’язання задач лінійного програмування. Це найкращий метод розв’язання задач лінійного програмування, який вимагає менше зусиль, ніж симплекс-метод.
Використовуючи цей метод, ми будуємо графіки всіх нерівностей, які піддаються обмеженням у заданих задачах лінійного програмування. Як тільки всі нерівності даної LPP будуть нанесені на графік XY, спільна область усіх нерівностей дає оптимальний розв’язок. Розраховуються всі кутові точки допустимої області та обчислюється значення цільової функції в усіх цих точках, а потім, порівнюючи ці значення, ми отримуємо оптимальне рішення LPP.
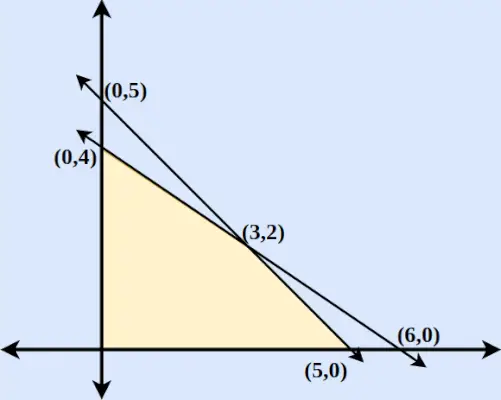
Приклад: знайдіть максимальне та мінімальне значення z = 6x + 9y, коли умови обмеження:
- 2x + 3y ≤ 12
- x і y ≥ 0
- x + y ≤ 5
рішення:
Крок 1 : спочатку перетворіть нерівності на нормальні рівняння. Отже, рівняння будуть такими: 2x+3y = 0, x = 0, y = 0 і x + y = 5.
Крок 2 : Знайдіть точки, в яких 2x + 3y і x + y = 5 перетинають вісь x і вісь y. Щоб знайти точку перетину осі x, поставте y = 0 у відповідне рівняння та знайдіть точку. Так само для точок перетину осі y поставте x = 0 у відповідному рівнянні.
Крок 3 : Намалюйте дві лінії, що перетинають вісь x і вісь y. Ми знаходимо, що дві осі перетинають одна одну в точці (3,2).
Крок 4 : Для x ≥ 0 і y ≥ 0 ми знаходимо, що дотримуються обидві нерівності. Таким чином, область включатиме область області, обмежену двома осями та обома лініями, включаючи початок координат. Побудована область показана на малюнку нижче.
Крок 5 : Знайдіть Z для кожної точки, максимумів і мінімумів.
Координати Z = 6x + 9y (0,5) Z = 45 (0,4) Z = 36 (5,0) Z = 30 (6,0) Z = 36 (3.2) Z = 36 Отже, ми знаходимо, що Z = 6x + 9y є максимальним при (0,5) і мінімальним при (5,0).
Програми лінійного програмування
Лінійне програмування має застосування в різних областях. Він використовується для визначення мінімальної вартості процесу, коли задано всі обмеження задач. Він використовується для оптимізації транспортних витрат транспортного засобу тощо. Різноманітні застосування лінійного програмування
Машинобудування
Машинобудівна промисловість використовує лінійне програмування для вирішення проектних і виробничих проблем і для отримання максимального результату за заданих умов.
Виробничі галузі
Виробничі галузі використовують лінійне програмування, щоб максимізувати прибуток компаній і зменшити витрати на виробництво.
Енергетичні галузі
Енергетичні компанії використовують лінійне програмування для оптимізації виробництва.
Транспортні галузі
Лінійне програмування також використовується в транспортній галузі, щоб знайти шлях до мінімізації вартості транспортування.
Важливість лінійного програмування
Лінійне програмування має велике значення в різних галузях промисловості, воно максимізує вихідне значення, мінімізуючи вхідні значення відповідно до різних обмежень.
LP дуже застосовний, коли у нас є кілька умов під час розв’язування задачі, і ми повинні оптимізувати результат проблеми, тобто ми повинні знайти мінімальне або максимальне значення відповідно до даної умови.
Детальніше,
- Лінійні нерівності
- Алгебраїчне розв’язування лінійних нерівностей
Задачі лінійного програмування
Проблема 1: Компанія виробляє та продає два типи продукції, а собівартість виробництва кожної одиниці a і b становить 200 і 150 рупій відповідно, кожна одиниця продукту дає прибуток 20 рупій, а кожна одиниця продукту b дає прибуток 15 рупій від продажу. . Компанія оцінює, що місячний попит на А та Б становить максимум одиниці зібраного врожаю в усьому виробничому бюджеті на місяць, встановленому в 50 000 рупій. Скільки одиниць має виготовити компанія, щоб отримати максимальний прибуток від своїх місячних продажів від і b?
рішення:
Нехай x = кількість одиниць типу A
y = кількість одиниць типу B
Максимізувати Z = 40x + 50y
З дотриманням обмежень
3x + y ≤ 9
x + 2y ≤ 8
і x, y ≥ 0
Розглянемо рівняння,
3x + y = 9
х = 3
y = 0
і x + 2y = 8
як вимкнути режим розробника на androidх = 8
y = 0
Тепер ми можемо визначити максимальне значення Z, оцінивши значення Z у чотирьох точках (вершинах), як показано нижче
Вершини
Z = 40x + 50y
(0, 0)
Z = 40 × 0 + 50 × 0 = рупій. 0
(3, 0)
Z = 40 × 3 + 50 × 0 = рупій. 120
(0, 4)
Z = 40 × 0 + 50 × 4 = рупій. 200
(23)
Z = 40 × 2 + 50 × 3 = рупій. 230
Максимальний прибуток, Z = рупій. 230
∴ Кількість одиниць типу A дорівнює 2, а кількість одиниць типу B дорівнює 3.
Проблема 2: Максимізувати Z = 3x + 4y.
З урахуванням обмежень x + y ≤ 450, 2x + y ≤ 600 і x, y ≤ 0.
рішення:
Маємо з даного
Обмеження (1)
X + Y = 450
Поклавши x = 0, ⇒ 0 + y = 450 ⇒ y = 450
Поклавши y = 0, ⇒ x + 0 = 450 ⇒ x = 450
від, Обмеження (2)
2x + y = 600
Поклавши x = 0, ⇒ 0 + y = 600 ⇒ y = 600
Поклавши y = 0, ⇒ 2x + 0 = 600 ⇒ x = 300
Тепер у нас є координати точки Z = 3x + 4y
| Вершини | Z = 3x + 4y |
|---|---|
| (0, 0) | Z = 3 × 0 + 4 × 0 = 0 |
| (300, 0) | Z = 3 × 300 + 4 × 0 = 900 |
| (150, 300) | Z = 3 × 150 + 4 × 300 = 1650 |
| (0, 450) | Z = 3 × 0 + 4 × 450 = 1800 |
Тому оптимальний максимум рішення Z = 1800 при координаті x = 0 і y = 450. Графік наведено нижче.

Сучасні програми лінійного програмування
Лінійне програмування, потужна математична техніка, використовується для вирішення задач оптимізації в різних галузях промисловості. Ось кілька сучасних програм:
- Оптимізація ланцюга поставок : Лінійне програмування допомагає компаніям мінімізувати витрати та максимізувати ефективність своїх ланцюгів поставок. Він використовується для визначення найбільш рентабельних маршрутів транспортування, складських операцій і стратегій управління запасами.
- Енергетичний менеджмент : В енергетичному секторі лінійне програмування використовується для оптимізації поєднання методів виробництва енергії. Це включає збалансування традиційних джерел енергії з відновлюваними, щоб зменшити витрати та вплив на навколишнє середовище, задовольнивши попит.
- Проектування телекомунікаційних мереж : Лінійне програмування допомагає проектувати ефективні телекомунікаційні мережі. Це допомагає у розподілі пропускної здатності, проектуванні мережевих макетів і оптимізації потоку даних для забезпечення високошвидкісного зв’язку за менших витрат.
- Фінансове планування : Підприємства та фінансові аналітики використовують лінійне програмування для оптимізації портфеля, управління ризиками та бюджетування капіталу. Це допомагає приймати інвестиційні рішення, які максимізують прибуток і мінімізують ризик.
- Логістика охорони здоров'я : в охороні здоров’я лінійне програмування застосовується для оптимізації розподілу ресурсів, таких як лікарняні ліжка, медичний персонал і обладнання. Це надзвичайно важливо для покращення догляду за пацієнтами, скорочення часу очікування та ефективного управління витратами.
- Оптимізація виробничого процесу : Лінійне програмування використовується для визначення оптимальних рівнів виробництва для кількох продуктів на виробничому підприємстві з урахуванням таких обмежень, як робоча сила, матеріали та доступність машин.
- Планування сільського господарства : Фермери та планувальники сільського господарства використовують лінійне програмування, щоб прийняти рішення щодо вибору культур, землекористування та розподілу ресурсів для максимізації врожайності та прибутку при збереженні ресурсів.
- Розклад екіпажу авіакомпанії : Авіакомпанії використовують лінійне програмування для ефективного планування екіпажів, гарантуючи, що персонал на рейсах відповідає правилам, і мінімізуючи експлуатаційні витрати.
Ці програми демонструють універсальність і потужність лінійного програмування у вирішенні складних задач оптимізації в різних секторах, демонструючи його актуальність у сучасному світі, що керується даними.
Лінійне програмування в дослідженні операцій
- Основний інструмент : Лінійне програмування є основоположним інструментом у дослідженні операцій для оптимізації ресурсів.
- Прийняття рішень : допомагає приймати найкращі рішення щодо розподілу ресурсів, максимізації прибутків або мінімізації витрат.
- Широке застосування : використовується в різних сферах, таких як логістика, виробництво, фінанси та охорона здоров’я для вирішення складних проблем.
- Моделювання проблем реального світу : перетворює проблеми реального світу в математичні моделі для пошуку найефективніших рішень.
Симплексний метод
- Алгоритм оптимізації : Симплексний метод — це потужний алгоритм, який використовується в лінійному програмуванні для пошуку оптимального розв’язку лінійних нерівностей.
- Поетапний підхід : Він ітеративно рухається до найкращого рішення шляхом навігації по краях можливої області, визначеної обмеженнями.
- Ефективність : відомий своєю ефективністю у вирішенні великомасштабних задач лінійного програмування.
- Універсальність : Застосовується в різних областях, таких як планування дієти, мережеві потоки, планування виробництва тощо, демонструючи свою універсальність.
Лінійне програмування – поширені запитання
Що таке лінійне програмування?
Лінійне програмування — це математична концепція, яка використовується для оптимізації даної лінійної задачі, яка має низку обмежень. За допомогою лінійного програмування ми знаходимо оптимальний вихід даної задачі
Що таке задачі лінійного програмування?
Задачі лінійного програмування (LPP) - це задачі, які дають оптимальний розв'язок заданих умов.
Що таке формула лінійного програмування?
Загальні формули лінійного програмування:
- Цільова функція: Z = ax + by
- Обмеження: px + qy ≤ r, sx + ty ≤ u
- Невід’ємні обмеження: x ≥ 0, y ≥ 0
Які існують типи лінійного програмування?
Різні типи методів лінійного програмування:
- Лінійне програмування симплексним методом
- Лінійне програмування методом R
- Лінійне програмування графічним методом
Які вимоги до лінійного програмування?
Різні вимоги задач лінійного програмування:
- Лінійність
- Цільова функція
- обмеження
- Ненегативність
Які переваги лінійного програмування?
Різні переваги лінійного програмування:
- Він забезпечує оптимальне вирішення будь-якої лінійної задачі.
- Він простий у використанні та завжди дає стабільні результати
- Це допомагає максимізувати прибуток і зменшити вхідні витрати.