Обмеження традиційних бінарних дерев пошуку можуть засмучувати. Зустрічайте B-Tree, багатофункціональну структуру даних, яка може легко обробляти величезні обсяги даних. Коли справа доходить до зберігання та пошуку великих обсягів даних, традиційні бінарні дерева пошуку можуть стати непрактичними через їх низьку продуктивність і високе використання пам’яті. B-дерева, також відомі як B-дерева або збалансоване дерево, є типом самобалансуючого дерева, яке було спеціально розроблено для подолання цих обмежень.
На відміну від традиційних бінарних дерев пошуку, B-дерева характеризуються великою кількістю ключів, які вони можуть зберігати в одному вузлі, тому вони також відомі як великі ключові дерева. Кожен вузол B-дерева може містити кілька ключів, що дозволяє дереву мати більший коефіцієнт розгалуження і, отже, меншу висоту. Така невелика висота призводить до меншого введення-виведення диска, що призводить до швидшого пошуку та операцій вставки. B-Trees особливо добре підходять для систем зберігання, які мають повільний доступ до великих даних, таких як жорсткі диски, флеш-пам'ять і компакт-диски.
B-Trees підтримує баланс, гарантуючи, що кожен вузол має мінімальну кількість ключів, тому дерево завжди збалансоване. Цей баланс гарантує, що складність часу для таких операцій, як вставка, видалення та пошук, завжди дорівнює O(log n), незалежно від початкової форми дерева.
Часова складність B-Tree:
| пан ні | Алгоритм | Часова складність |
|---|---|---|
| 1. | Пошук | O(log n) |
| 2. | Вставка | O(log n) |
| 3. | Видалити | O(log n) |
Примітка: n – загальна кількість елементів у B-дереві
перетворення nfa в dfa
Властивості B-Tree:
- Всі листочки знаходяться на одному рівні.
- B-дерево визначається терміном мінімальний ступінь t ‘. Значення ' t ' залежить від розміру блоку диска.
- Кожен вузол, крім кореня, повинен містити щонайменше t-1 ключів. Корінь може містити мінімум 1 ключ.
- Усі вузли (включно з коренем) можуть містити щонайбільше ( 2*t – 1 ) ключі.
- Кількість дітей вузла дорівнює кількості ключів у ньому плюс 1 .
- Усі ключі вузла відсортовані в порядку зростання. Дитина між двома ключами k1 і k2 містить усі ключі в діапазоні від k1 і k2 .
- B-дерево росте та зменшується від кореня, на відміну від бінарного дерева пошуку. Бінарні дерева пошуку ростуть униз і також зменшуються вниз.
- Як і в інших збалансованих бінарних деревах пошуку, час пошуку, вставки та видалення становить O (log n).
- Вставлення вузла в B-дерево відбувається лише в листовому вузлі.
Нижче наведено приклад B-дерева мінімального порядку 5
Примітка: що в практичних B-деревах значення мінімального замовлення значно перевищує 5.

Ми бачимо на наведеній вище діаграмі, що всі листові вузли знаходяться на одному рівні, а всі не-листя не мають порожнього піддерева і мають ключі на один менше, ніж кількість їх дочірніх елементів.
Цікаві факти про B-дерева:
- Мінімальна висота B-дерева, яке може існувати з n кількістю вузлів і m є максимальною кількістю дочірніх елементів вузла, дорівнює:
- Максимальна висота B-дерева, яке може існувати з n кількістю вузлів і t є мінімальною кількістю дочірніх елементів, які може мати некореневий вузол, становить:
і
Обхід у B-Tree:
Обхід також схожий на обхід у порядку бінарного дерева. Ми починаємо з крайнього лівого дочірнього елемента, рекурсивно друкуємо крайнього лівого дочірнього елемента, потім повторюємо той самий процес для решти дочірніх елементів і ключів. Зрештою, рекурсивно надрукуйте крайню праву дочірню частину.
Операція пошуку в B-Tree:
Пошук схожий на пошук у бінарному дереві пошуку. Нехай шуканий ключ є k.
- Почніть з кореня і рекурсивно переходьте вниз.
- Для кожного відвіданого нелистового вузла,
- Якщо вузол має ключ, ми просто повертаємо вузол.
- В іншому випадку ми повертаємося до відповідного дочірнього елемента (дочірнього елемента, який стоїть перед першим більшим ключем) вузла.
- Якщо ми досягаємо кінцевого вузла і не знаходимо k у листовому вузлі, повертаємо NULL.
Пошук у B-дереві подібний до пошуку у бінарному дереві. Алгоритм аналогічний і працює з рекурсією. На кожному рівні пошук оптимізується так, якщо значення ключа немає в діапазоні батьківського елемента, тоді ключ присутній в іншій гілці. Оскільки ці значення обмежують пошук, вони також відомі як обмежувальні значення або значення розділення. Якщо ми досягнемо кінцевого вузла і не знайдемо потрібний ключ, тоді він відобразить NULL.
Алгоритм пошуку елемента в B-дереві:-
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->key[i]) {> >i++;> >}> >if> (i n && k == x->ключ[i]) {> >return> x;> >}> >if> (x->лист) {> >return> nullptr;> >}> >return> BtreeSearch(x->child[i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.key[i]: i += 1 якщо i та k == x.key[i]: повернути x якщо x.leaf: повернути Немає повернути BtreeSearch(x.child[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
приклади:
підрядок javascript trim
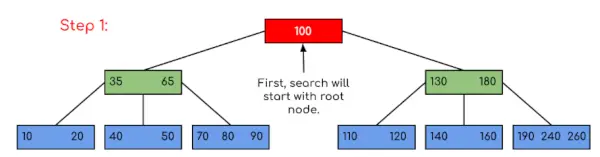
введення: Пошук 120 у заданому B-дереві.
рішення:
команда touch в linux
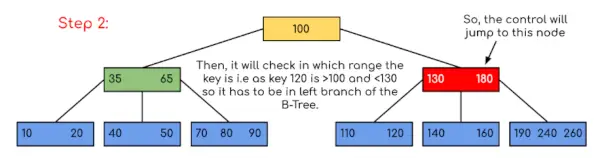
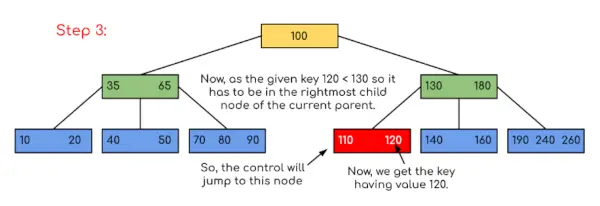
У цьому прикладі ми бачимо, що наш пошук було скорочено лише обмеженням шансів, коли ключ, що містить значення, може бути присутнім. Подібним чином, якщо в наведеному вище прикладі ми шукаємо 180, тоді керування зупиниться на кроці 2, оскільки програма виявить, що ключ 180 присутній у поточному вузлі. І аналогічно, якщо шукати 90, то як 90 <100, то він автоматично перейде до лівого піддерева, і тому потік керування відбуватиметься так само, як показано у прикладі вище.
Нижче наведено реалізацію вищезазначеного підходу:
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->траверс();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->пошук(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->траверс(); cout<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->траверс(); } // Функція для пошуку ключа k у піддереві, кореневому цьому вузлі BTreeNode* BTreeNode::search(int k) { // Знайти перший ключ, більший або рівний k int i = 0; while (i keys[i]) i++; // Якщо знайдений ключ дорівнює k, повернути цей вузол if (keys[i] == k) return this; // Якщо ключ тут не знайдено, і це кінцевий вузол if (leaf == true) return NULL; // Перехід до відповідної дитини return C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>=> 0> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 і k[0] 0]: i -= 1 i += 1 if len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Розділити нащадок def split_child(self, x, i): t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] якщо не y.leaf: z.child = y.child[t: 2 * t] y. child = y.child[0: t - 1] # Вивести дерево def print_tree(self, x, l=0): print('Рівень ', l, ' ', len(x.keys), end=':') для i в x.keys: print(i, end=' ') print() l += 1 якщо len(x.child)> 0: для i в x.child: self.print_tree(i, l) # Ключ пошуку в дереві def search_key(self, k, x=None): якщо x не є None: i = 0, тоді як i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Примітка: Наведений вище код не містить програми драйвера. Ми розглянемо повну програму в нашій наступній публікації Вставка B-дерева .
Існують дві конвенції для визначення B-дерева: одна — за мінімальним ступенем, друга — за порядком. Ми дотримуємося конвенції про мінімальний ступінь і будемо дотримуватися цього в наступних публікаціях на B-Tree. Імена змінних, які використовуються у наведеній вище програмі, також залишаються незмінними
перетворення рядка в java
Застосування B-Trees:
- Він використовується у великих базах даних для доступу до даних, що зберігаються на диску
- Пошук даних у наборі даних може бути досягнутий за значно менший час за допомогою B-Tree
- За допомогою функції індексування можна досягти багаторівневої індексації.
- Більшість серверів також використовують підхід B-дерева.
- B-дерева використовуються в системах САПР для організації та пошуку геометричних даних.
- B-дерева також використовуються в інших сферах, таких як обробка природної мови, комп’ютерні мережі та криптографія.
Переваги B-Trees:
- B-Trees мають гарантовану часову складність O(log n) для основних операцій, таких як вставка, видалення та пошук, що робить їх придатними для великих наборів даних і програм реального часу.
- B-дерева самобалансуються.
- Високий паралелізм і висока пропускна здатність.
- Ефективне використання сховища.
Недоліки B-Trees:
- B-дерева базуються на дискових структурах даних і можуть мати високе використання диска.
- Не найкраще для всіх випадків.
- Повільно порівняно з іншими структурами даних.
Вставка та видалення:
Вставка B-дерева
Видалення B-дерева