NFA може мати нуль, один або більше ніж один хід із заданого стану на заданому вхідному символі. NFA також може мати NULL ходи (ходи без вхідного символу). З іншого боку, DFA має один і тільки один хід із заданого стану на заданому вхідному символі.

Кроки для перетворення NFA на DFA:

Крок 1: Перетворіть даний NFA на еквівалентну таблицю переходів
Щоб перетворити NFA на еквівалентну таблицю переходів, нам потрібно перерахувати всі стани, вхідні символи та правила переходу. Правила переходу представлені у вигляді матриці, де рядки представляють поточний стан, стовпці представляють вхідний символ, а комірки представляють наступний стан.

Крок 2: Створіть початковий стан DFA
Початковий стан DFA — це набір усіх можливих початкових станів у NFA. Цей набір називається епсилон-закриттям початкового стану NFA. Епсилон-замикання — це набір усіх станів, які можуть бути досягнуті з початкового стану, дотримуючись переходів епсилон (?).

ipconfig для ubuntu

Крок 3: Створіть таблицю переходів DFA
Таблиця переходів DFA схожа на таблицю переходів NFA, але замість окремих станів рядки та стовпці представляють набори станів. Для кожного вхідного символу відповідна комірка в таблиці переходів містить епсилон-замикання набору станів, отриманих шляхом дотримання правил переходу в таблиці переходів NFA.

Крок 4: Створіть остаточні стани DFA
Кінцеві стани DFA — це набори станів, які містять принаймні один кінцевий стан із NFA.

Крок 5. Спростіть DFA
DFA, отриманий на попередніх кроках, може містити непотрібні стани та переходи. Щоб спростити DFA, ми можемо використати такі методи:

створення столів з латексу

• Видалити недосяжні стани: стани, які не можна отримати з початкового стану, можна видалити з DFA.
• Видалити мертві стани: стани, які не можуть привести до кінцевого стану, можна видалити з DFA.
• Об’єднати еквівалентні стани: стани, які мають однакові правила переходу для всіх вхідних символів, можна об’єднати в один стан.

Крок 6: повторюйте кроки 3-5, доки подальше спрощення не стане можливим
Після спрощення DFA ми повторюємо кроки 3-5, доки подальше спрощення не стане можливим. Остаточний отриманий DFA є мінімізованим DFA, еквівалентним заданому NFA.

приклад: Розглянемо наступний NFA, показаний на малюнку 1.

Нижче наведено різні параметри для NFA. Q = { q0, q1, q2 } ? = ( a, b ) F = { q2 } ? (Перехідна функція NFA)

оновлення від join sql

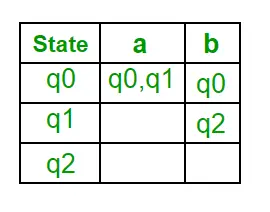
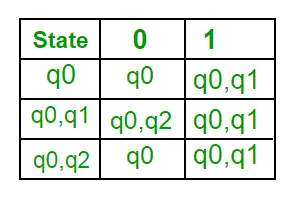
Крок 1: Q’ = ? Крок 2: Q’ = {q0} Крок 3: Для кожного стану в Q’ знайдіть стани для кожного вхідного символу. Наразі стан у Q’ дорівнює q0, знайдіть переміщення від q0 на вхідному символі a та b за допомогою функції переходу NFA та оновіть таблицю переходів DFA. ?’ (функція переходу DFA)

Тепер { q0, q1 } буде розглядатися як єдиний стан. Оскільки його запис не в Q’, додайте його до Q’. Отже, Q' = { q0, { q0, q1 } } Тепер переміщення зі стану { q0, q1 } на різних вхідних символах відсутні в таблиці переходів DFA, ми обчислимо це так: ?' ( { q0, q1 } , а ) = ? ( q0, a ) ? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? ( q0, b ) ? ? ( q1, b ) = { q0, q2 } Тепер ми оновимо таблицю переходів DFA. ?’ (функція переходу DFA)

Тепер { q0, q2 } буде розглядатися як один стан. Оскільки його запис не в Q’, додайте його до Q’. Отже, Q' = { q0, { q0, q1 }, { q0, q2 } } Тепер переміщення зі стану {q0, q2} на різних вхідних символах відсутні в таблиці переходів DFA, ми обчислимо це так: ?' ( { q0, q2 }, a ) = ? ( q0, a ) ? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? ( q0, b ) ? ? ( q2, b ) = { q0 } Тепер ми оновимо таблицю переходів DFA. ?’ (функція переходу DFA)

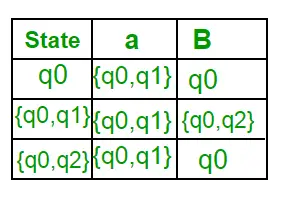
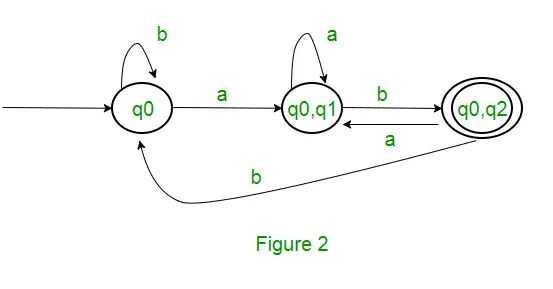
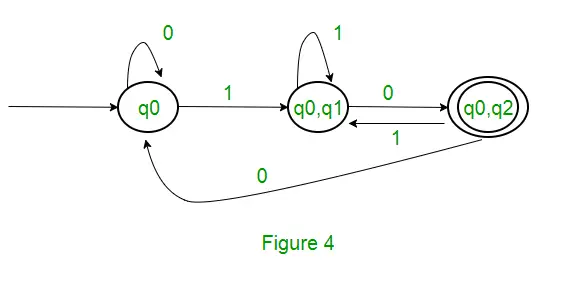
Оскільки новий стан не створено, ми завершили перетворення. Остаточним станом DFA буде стан, який має q2 як компонент, тобто { q0, q2 } Нижче наведено різні параметри для DFA. Q’ = { q0, { q0, q1 }, { q0, q2 } } ? = ( a, b ) F = { { q0, q2 } } і функція переходу ?’, як показано вище. Остаточний DFA для вищезазначеного NFA показано на малюнку 2.

Примітка : Іноді буває непросто перетворити регулярний вираз у DFA. Спочатку ви можете перетворити регулярний вираз на NFA, а потім NFA на DFA.

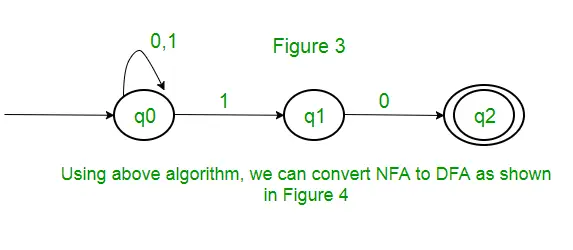
питання: Кількість станів у мінімальному детермінованому скінченному автоматі, що відповідає регулярному виразу (0 + 1)* (10), становить ____________.

рішення: Спочатку ми створимо NFA для наведеного вище виразу. Щоб зробити NFA для (0 + 1)*, NFA буде в тому самому стані q0 на вхідному символі 0 або 1. Потім для конкатенації ми додамо два ходи (q0 до q1 для 1 і q1 до q2 для 0), як показано на малюнку 3.

b+ дерева

Цю статтю надав Sonal Tuteja.