Алгоритм Форда-Фулкерсона є широко використовуваним алгоритмом для вирішення проблеми максимального потоку в потоковій мережі. Проблема максимального потоку передбачає визначення максимального обсягу потоку, який можна надіслати від вершини-джерела до вершини-приймача в спрямованому зваженому графі з урахуванням обмежень пропускної здатності на ребрах.
Алгоритм працює, ітеративно знаходячи шлях доповнення, який є шляхом від джерела до поглинача на залишковому графі, тобто графіку, отриманому шляхом віднімання поточного потоку від пропускної здатності кожного краю. Потім алгоритм збільшує потік уздовж цього шляху на максимально можливу величину, яка є мінімальною пропускною здатністю ребер уздовж шляху.
проблема:
Дано граф, який представляє мережу потоків, де кожне ребро має пропускну здатність. Крім того, дано дві вершини джерело «s» і раковина ‘t’ на графіку знайдіть максимально можливий потік від s до t із такими обмеженнями:
- Потік на краю не перевищує задану пропускну здатність краю.
- Вхідний потік дорівнює вихідному для кожної вершини, крім s і t.
Наприклад, розглянемо наступний графік із книги CLRS.
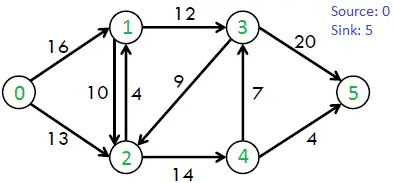
Максимальний можливий потік на наведеному вище графіку становить 23.

Необхідна умова: Вступ до проблеми максимального потоку
Алгоритм Форда-Фулкерсона
Ось проста ідея алгоритму Форда-Фулкерсона:
- Почніть з початкового потоку як 0.
- Хоча існує шлях доповнення від джерела до приймача:
- Знайдіть додатковий шлях за допомогою будь-якого алгоритму пошуку шляху, наприклад пошуку в ширину або в глибину.
- Визначте обсяг потоку, який можна направити вздовж доповнюючого шляху, який є мінімальною залишковою потужністю по краях шляху.
- Збільште потік уздовж шляху збільшення на визначену величину.
- Поверніть максимальний потік.
Часова складність: Часова складність наведеного вище алгоритму становить O(max_flow * E). Ми запускаємо цикл, поки є шлях доповнення. У гіршому випадку ми можемо додати 1 одиничний потік на кожній ітерації. Тому часова складність стає O(max_flow * E).
Як реалізувати наведений вище простий алгоритм?
Давайте спочатку визначимо концепцію Residual Graph, яка потрібна для розуміння реалізації.
Графік залишків потокової мережі – це графік, який вказує на додатковий можливий потік. Якщо в графі залишків є шлях від джерела до поглинача, то можна додати потік. Кожне ребро залишкового графа має значення, яке називається залишкова ємність що дорівнює початковій ємності краю за вирахуванням потоку струму. Залишкова ємність - це в основному поточна ємність краю.
Тепер поговоримо про деталі впровадження. Залишкова ємність дорівнює 0, якщо між двома вершинами залишкового графа немає ребра. Ми можемо ініціалізувати залишковий графік як початковий графік, оскільки початкового потоку немає, а початкова залишкова ємність дорівнює початковій ємності. Щоб знайти шлях доповнення, ми можемо зробити BFS або DFS залишкового графіка. Ми використали BFS у наведеній нижче реалізації. Використовуючи BFS, ми можемо дізнатися, чи є шлях від джерела до поглинача. BFS також створює масив parent[]. Використовуючи масив parent[], ми переходимо через знайдений шлях і знаходимо можливий потік через цей шлях, знаходячи мінімальну залишкову ємність уздовж шляху. Пізніше ми додаємо знайдений шлях до загального потоку.
Важливо те, що нам потрібно оновити залишкові потужності на графіку залишків. Ми віднімаємо потік шляху від усіх країв уздовж шляху та додаємо потік шляху вздовж зворотних країв. Нам потрібно додати потік шляху вздовж зворотних країв, тому що пізніше може знадобитися надіслати потік у зворотному напрямку (див. наступне посилання, наприклад).
Нижче наведено реалізацію алгоритму Форда-Фулкерсона. Для простоти графік представлено у вигляді двовимірної матриці.
C++
// C++ program for implementation of Ford Fulkerson> // algorithm> #include> #include> #include> #include> using> namespace> std;> // Number of vertices in given graph> #define V 6> /* Returns true if there is a path from source 's' to sink> >'t' in residual graph. Also fills parent[] to store the> >path */> bool> bfs(>int> rGraph[V][V],>int> s,>int> t,>int> parent[])> {> >// Create a visited array and mark all vertices as not> >// visited> >bool> visited[V];> >memset>(visited, 0,>sizeof>(visited));> >// Create a queue, enqueue source vertex and mark source> >// vertex as visited> >queue<>int>>q;> >q.push(s);> >visited[s] =>true>;> >parent[s] = -1;> >// Standard BFS Loop> >while> (!q.empty()) {> >int> u = q.front();> >q.pop();> >for> (>int> v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Якщо ми знайдемо з’єднання з вузлом-приймачем, // тоді в BFS більше немає сенсу. Ми // просто повинні встановити його батьківського елемента та можемо повернути // true if (v == t) { parent[ v] = u; повернути істину; } q.push(v); parent[v] = u; visited[v] = правда; } } } // Ми не досягли приймача в BFS, починаючи з джерела, тому // повертаємо false return false; } // Повертає максимальний потік від s до t у заданому графіку int fordFulkerson(int graph[V][V], int s, int t) { int u, v; // Створіть графік залишків і заповніть граф залишків // заданими ємностями у вихідному графіку як // залишкові ємності у графіку залишків int rGraph[V] [V]; // Залишковий графік, де rGraph[i][j] // вказує залишкову ємність ребра // від i до j (якщо ребро є. Якщо // rGraph[i][j] дорівнює 0, то його немає) for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; int parent[V]; // Цей масив заповнюється BFS і // зберігає шлях int max_flow = 0; // Спочатку потоку немає // Збільшити потік, поки є шлях від джерела до // sink while (bfs(rGraph, s, t, parent)) { // Знайти мінімальну залишкову ємність ребер вздовж // шляху, заповненого BFS. // знайдений максимальний потік int path_flow = INT_MAX; parent[v]; path_flow = min(path_flow, rGraph[u][v]); // оновити залишкові ємності ребер і // реверсувати ребра вздовж шляху для (v = t; v != s; v = parent[v]) { u = parent[v] -= path_flow; rGraph[v] += path_flow } // Додати потік шляху до загального потоку } // Повертає загальний потік return max_flow; } // Програма драйвера для тестування вищезазначених функцій int main() { // Давайте створимо графік, показаний у прикладі вище int graph[V][V] = { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7 , 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; cout<< 'The maximum possible flow is ' << fordFulkerson(graph, 0, 5); return 0; }> |
>
>
Java
c програма для порівняння рядків
// Java program for implementation of Ford Fulkerson> // algorithm> import> java.io.*;> import> java.lang.*;> import> java.util.*;> import> java.util.LinkedList;> class> MaxFlow {> >static> final> int> V =>6>;>// Number of vertices in graph> >/* Returns true if there is a path from source 's' to> >sink 't' in residual graph. Also fills parent[] to> >store the path */> >boolean> bfs(>int> rGraph[][],>int> s,>int> t,>int> parent[])> >{> >// Create a visited array and mark all vertices as> >// not visited> >boolean> visited[] =>new> boolean>[V];> >for> (>int> i =>0>; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited LinkedList queue = new LinkedList(); queue.add(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.size() != 0) { int u = queue.poll(); for (int v = 0; v if (visited[v] == false && rGraph[u][v]>0) { // Якщо ми знайдемо з’єднання з // вузлом-приймачем, тоді // більше немає сенсу в BFS. Нам просто потрібно встановити його батьківського // і може повернути true if (v == t) { parent[ v] = u; повернути істину; } queue.add(v); parent[v] = u; visited[v] = правда; } } } // Ми не досягли приймача в BFS, починаючи з джерела, // тому повертаємо false return false; } // Повертає максимальний потік від s до t у заданому // графіку int fordFulkerson(int graph[][], int s, int t) { int u, v; // Створіть залишковий граф і заповніть залишковий // граф заданими ємностями у вихідному графі // як залишкові ємності в залишковому графі // Залишковий граф, де rGraph[i][j] вказує // залишкову ємність ребра від i до j (якщо // є ребро. Якщо rGraph[i][j] дорівнює 0, то // немає) int rGraph[][] = new int[V][V]; for (u = 0; u for (v = 0; v rGraph[u][v] = graph[u][v]; // Цей масив заповнюється BFS і для зберігання шляху int parent[] = new int[ V]; int max_flow = 0; // Спочатку немає потоку // Збільшити потік, поки є шлях від джерела // до приймача while (bfs(rGraph, s, t, parent)) { // Знайти мінімальну залишкову ємність // вздовж шляху, заповненого BFS. // Знайти максимальний потік через знайдений шлях int path_flow = Integer.MAX_VALUE; ]) { u = parent[v]; path_flow = Math.min(path_flow, rGraph[u][v]); v != s; v = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] += path_flow; } // Додати шлях до загального flow max_flow += path_flow; } // Повертає загальний потік return max_flow } // Програма драйвера для перевірки вищезазначених функцій public static void main(String[] args) throws java.lang.Exception { // Створимо показаний графік у наведеному вище прикладі int graph[][] = new int[][] { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 }, { 0, 4 , 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 }, { 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } }; MaxFlow m = новий MaxFlow(); System.out.println('Максимальний можливий потік ' + m.fordFulkerson(graph, 0, 5)); } }> |
>
>
Python
# Python program for implementation> # of Ford Fulkerson algorithm> from> collections>import> defaultdict> # This class represents a directed graph> # using adjacency matrix representation> class> Graph:> >def> __init__(>self>, graph):> >self>.graph>=> graph># residual graph> >self>. ROW>=> len>(graph)> ># self.COL = len(gr[0])> >'''Returns true if there is a path from source 's' to sink 't' in> >residual graph. Also fills parent[] to store the path '''> >def> BFS(>self>, s, t, parent):> ># Mark all the vertices as not visited> >visited>=> [>False>]>*>(>self>.ROW)> ># Create a queue for BFS> >queue>=> []> ># Mark the source node as visited and enqueue it> >queue.append(s)> >visited[s]>=> True> ># Standard BFS Loop> >while> queue:> ># Dequeue a vertex from queue and print it> >u>=> queue.pop(>0>)> ># Get all adjacent vertices of the dequeued vertex u> ># If a adjacent has not been visited, then mark it> ># visited and enqueue it> >for> ind, val>in> enumerate>(>self>.graph[u]):> >if> visited[ind]>=>=> False> and> val>>0>:> ># If we find a connection to the sink node,> ># then there is no point in BFS anymore> ># We just have to set its parent and can return true> >queue.append(ind)> >visited[ind]>=> True> >parent[ind]>=> u> >if> ind>=>=> t:> >return> True> ># We didn't reach sink in BFS starting> ># from source, so return false> >return> False> > > ># Returns the maximum flow from s to t in the given graph> >def> FordFulkerson(>self>, source, sink):> ># This array is filled by BFS and to store path> >parent>=> [>->1>]>*>(>self>.ROW)> >max_flow>=> 0> # There is no flow initially> ># Augment the flow while there is path from source to sink> >while> self>.BFS(source, sink, parent) :> ># Find minimum residual capacity of the edges along the> ># path filled by BFS. Or we can say find the maximum flow> ># through the path found.> >path_flow>=> float>(>'Inf'>)> >s>=> sink> >while>(s !>=> source):> >path_flow>=> min> (path_flow,>self>.graph[parent[s]][s])> >s>=> parent[s]> ># Add path flow to overall flow> >max_flow>+>=> path_flow> ># update residual capacities of the edges and reverse edges> ># along the path> >v>=> sink> >while>(v !>=> source):> >u>=> parent[v]> >self>.graph[u][v]>->=> path_flow> >self>.graph[v][u]>+>=> path_flow> >v>=> parent[v]> >return> max_flow> > # Create a graph given in the above diagram> graph>=> [[>0>,>16>,>13>,>0>,>0>,>0>],> >[>0>,>0>,>10>,>12>,>0>,>0>],> >[>0>,>4>,>0>,>0>,>14>,>0>],> >[>0>,>0>,>9>,>0>,>0>,>20>],> >[>0>,>0>,>0>,>7>,>0>,>4>],> >[>0>,>0>,>0>,>0>,>0>,>0>]]> g>=> Graph(graph)> source>=> 0>; sink>=> 5> > print> (>'The maximum possible flow is %d '> %> g.FordFulkerson(source, sink))> # This code is contributed by Neelam Yadav> |
>
>
C#
// C# program for implementation> // of Ford Fulkerson algorithm> using> System;> using> System.Collections.Generic;> public> class> MaxFlow {> >static> readonly> int> V = 6;>// Number of vertices in> >// graph> >/* Returns true if there is a path> >from source 's' to sink 't' in residual> >graph. Also fills parent[] to store the> >path */> >bool> bfs(>int>[, ] rGraph,>int> s,>int> t,>int>[] parent)> >{> >// Create a visited array and mark> >// all vertices as not visited> >bool>[] visited =>new> bool>[V];> >for> (>int> i = 0; i visited[i] = false; // Create a queue, enqueue source vertex and mark // source vertex as visited List |
>
>
Javascript
> // Javascript program for implementation of Ford> // Fulkerson algorithm> // Number of vertices in graph> let V = 6;> // Returns true if there is a path from source> // 's' to sink 't' in residual graph. Also> // fills parent[] to store the path> function> bfs(rGraph, s, t, parent)> {> > >// Create a visited array and mark all> >// vertices as not visited> >let visited =>new> Array(V);> >for>(let i = 0; i visited[i] = false; // Create a queue, enqueue source vertex // and mark source vertex as visited let queue = []; queue.push(s); visited[s] = true; parent[s] = -1; // Standard BFS Loop while (queue.length != 0) { let u = queue.shift(); for(let v = 0; v { if (visited[v] == false && rGraph[u][v]>0) { // Якщо ми знайдемо з’єднання з // вузлом-приймачем, тоді // більше немає сенсу в BFS. Нам просто потрібно встановити його батьківського // і може повернути true if (v == t) { parent[ v] = u; повернути істину; } queue.push(v); parent[v] = u; visited[v] = правда; } } } // Ми не досягли приймача в BFS, починаючи // з джерела, тому повертаємо false return false; } // Повертає максимальний потік від s до t у // заданому графіку function fordFulkerson(graph, s, t) { let u, v; // Створіть граф залишків і заповніть // граф залишків заданими ємностями // у вихідному графіку як залишкові // ємності в графі залишків // Граф залишків, де rGraph[i][j] // вказує залишкову ємність краю / / від i до j (якщо є ребро. // Якщо rGraph[i][j] дорівнює 0, то його // немає) let rGraph = new Array(V); for(u = 0; u { rGraph[u] = new Array(V); for(v = 0; v rGraph[u][v] = graph[u][v]; } // Цей масив заповнюється BFS і зберегти шлях let parent = new Array(V); // Немає потоку спочатку let max_flow = 0; , parent) { // Знайти мінімальну залишкову ємність ребер // вздовж шляху, заповненого BFS. // Знайти максимальний потік через знайдений шлях ; v != s; v = parent[v]; path_flow = Math.min(path_flow, rGraph[u]); зворотні ребра вздовж шляху for(v = t; v != s; v = parent[v]) { u = parent[v]; rGraph[u][v] -= path_flow; rGraph[v][u] + = path_flow; } // Додати потік шляху до загального потоку max_flow } // Повернути загальний потік max_flow } // Створимо графік, показаний у прикладі вище let graph = [ 0 , 16, 13, 0, 0, 0 ], [ 0, 0, 10, 12, 0, 0 ], [ 0, 4, 0, 0, 14, 0 ], [ 0, 0, 9, 0, 0 , 20 ], [ 0, 0, 0, 7, 0, 4 ], [ 0, 0, 0, 0, 0, 0 ] ]; document.write('Максимальний можливий потік ' + fordFulkerson(graph, 0, 5)); // Цей код створено avanitrachhadiya2155> |
>
>Вихід
The maximum possible flow is 23>
Часова складність: O(|V| * E^2) , де E — кількість ребер, а V — кількість вершин.
Просторова складність: O(V), як ми створили чергу.
Вищеописана реалізація алгоритму Форда Фулкерсона називається Алгоритм Едмондса-Карпа . Ідея Едмондса-Карпа полягає у використанні BFS у реалізації Ford Fulkerson, оскільки BFS завжди вибирає шлях із мінімальною кількістю ребер. Коли використовується BFS, часова складність у найгіршому випадку може бути зменшена до O(VE2). У наведеній вище реалізації використовується представлення матриці суміжності, хоча BFS приймає O(V2) часу, часова складність вищевказаної реалізації становить O(EV3) (Див Книга CLRS для доказу складності часу)
Це важлива проблема, оскільки вона виникає в багатьох практичних ситуаціях. Приклади включають максимізацію транспортування з заданими обмеженнями трафіку, максимізацію потоку пакетів у комп’ютерних мережах.
Алгоритм Дінка для максимального потоку.
Вправа:
Змініть наведену вище реалізацію так, щоб вона працювала в O(VE2) час.
