The Алгоритм Флойда-Воршалла , названий на честь своїх творців Роберт Флойд і Стівен Уоршалл , є фундаментальним алгоритмом в інформатиці та теорії графів. Він використовується для пошуку найкоротших шляхів між усіма парами вузлів у зваженому графі. Цей алгоритм є високоефективним і може обробляти графіки з обома позитивний і п негативні ваги країв , що робить його універсальним інструментом для вирішення широкого кола проблем з мережею та підключенням.
Зміст
- Алгоритм Флойда Воршелла
- Ідея алгоритму Флойда Воршелла
- Алгоритм Флойда Уоршалла Алгоритм
- Псевдокод алгоритму Флойда Воршелла
- Ілюстрація алгоритму Флойда Воршелла
- Аналіз складності алгоритму Флойда Уоршолла
- Чому алгоритм Флойда-Варшалла кращий для щільних графів, а не для розріджених?
- Важливі запитання для співбесіди, пов’язані з Флойдом-Воршаллом
- Застосування алгоритму Флойда-Воршалла в реальному світі
Алгоритм Флойда Уоршолла:
The Алгоритм Флойда Воршелла це алгоритм найкоротшого шляху з усіма парами на відміну від Дейкстра і Беллман Форд які є алгоритмами найкоротшого шляху з одного джерела. Цей алгоритм працює як для спрямований і неорієнтований зважений графіки. Але це не працює для графів із від’ємними циклами (де сума ребер у циклі від’ємна). Це слідує Динамічне програмування підхід для перевірки кожного можливого шляху, що проходить через кожен можливий вузол, щоб обчислити найкоротшу відстань між кожною парою вузлів.
mylivecricket.in
Ідея алгоритму Флойда Воршелла:
Припустимо, у нас є графік G[][] з IN вершини з 1 до Н . Тепер ми маємо оцінити a матриця найкоротшого шляху[][] де s hortestPathMatrix[i][j] представляє найкоротший шлях між вершинами i і j .
Очевидно, найкоротший шлях між ними i до j буде мати деякі k кількість проміжних вузлів. Ідея алгоритму Флойда Уоршела полягає в обробці кожної вершини з 1 до Н як проміжний вузол один за одним.
На наступному малюнку показано наведену вище властивість оптимальної підструктури в алгоритмі Флойда Варшолла:
Алгоритм Флойда Уоршалла Алгоритм:
- На першому кроці ініціалізуйте матрицю рішення так само, як і матрицю вхідного графіка.
- Потім оновіть матрицю рішення, розглядаючи всі вершини як проміжні вершини.
- Ідея полягає в тому, щоб вибрати всі вершини одну за одною та оновити всі найкоротші шляхи, які включають вибрану вершину як проміжну вершину в найкоротшому шляху.
- Коли ми вибираємо номер вершини k як проміжну вершину ми вже розглянули вершини {0, 1, 2, .. k-1} як проміжні вершини.
- Для кожної пари (i, j) вихідної та кінцевої вершин відповідно, можливі два випадки.
- k не є проміжною вершиною на найкоротшому шляху від i до j . Ми зберігаємо цінність dist[i][j] так як є.
- k є проміжною вершиною на найкоротшому шляху від i до j . Ми оновлюємо значення dist[i][j] як dist[i][k] + dist[k][j], якщо dist[i][j]> dist[i][k] + dist[k][j]
Псевдокод алгоритму Флойда Воршелла:>
Для k = 0 до n – 1
Для i = 0 до n – 1
Для j = 0 до n – 1
Відстань[i, j] = min(Відстань[i, j], Відстань[i, k] + Відстань[k, j])де i = вихідний вузол, j = кінцевий вузол, k = проміжний вузол
Ілюстрація алгоритму Флойда Уоршолла:
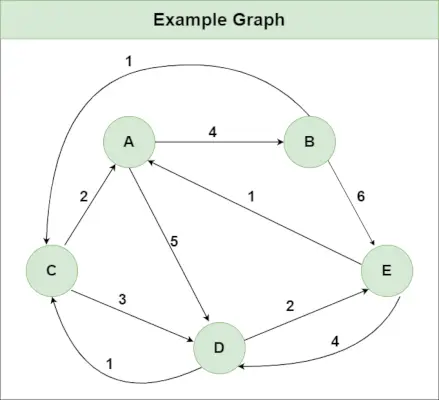
Рекомендована практика Спробуйте!Припустимо, у нас є графік, як показано на зображенні:
python перетворює байти на рядокКрок 1 : Ініціалізуйте матрицю Distance[][] за допомогою вхідного графіка так, щоб Distance[i][j]= вага краю від i до j , також Distance[i][j] = нескінченність, якщо немає краю від i до j.
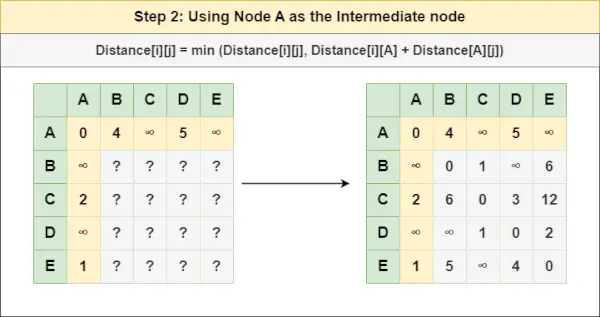
Крок 2 : Лікувати вузол А як проміжний вузол і обчислити відстань [][] для кожної пари вузлів {i,j} за формулою:
= Відстань[i][j] = мінімум (Відстань[i][j], (Відстань від i до А ) + (Відстань від А до j))
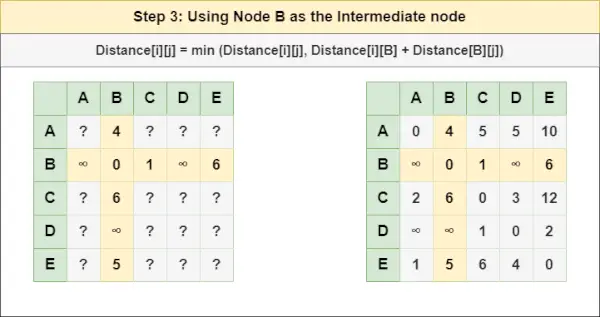
= Відстань[i][j] = мінімум (Відстань[i][j], Відстань[i][ А ] + Відстань[ А ][j])Крок 3 : Лікувати вузол Б як проміжний вузол і обчислити відстань [][] для кожної пари вузлів {i,j} за формулою:
= Відстань[i][j] = мінімум (Відстань[i][j], (Відстань від i до Б ) + (Відстань від Б до j))
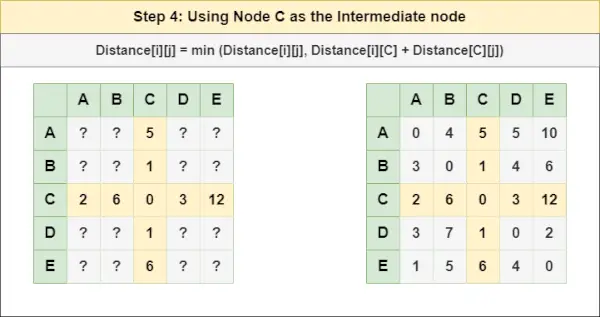
= Відстань[i][j] = мінімум (Відстань[i][j], Відстань[i][ Б ] + Відстань[ Б ][j])Крок 4 : Лікувати вузол C як проміжний вузол і обчислити відстань [][] для кожної пари вузлів {i,j} за формулою:
= Відстань[i][j] = мінімум (Відстань[i][j], (Відстань від i до C ) + (Відстань від C до j))
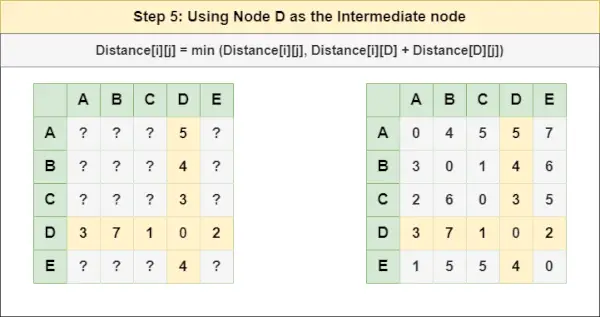
= Відстань[i][j] = мінімум (Відстань[i][j], Відстань[i][ C ] + Відстань[ C ][j])Крок 5 : Лікувати вузол Д як проміжний вузол і обчислити відстань [][] для кожної пари вузлів {i,j} за формулою:
наскільки великий екран мого комп'ютера= Відстань[i][j] = мінімум (Відстань[i][j], (Відстань від i до Д ) + (Відстань від Д до j))
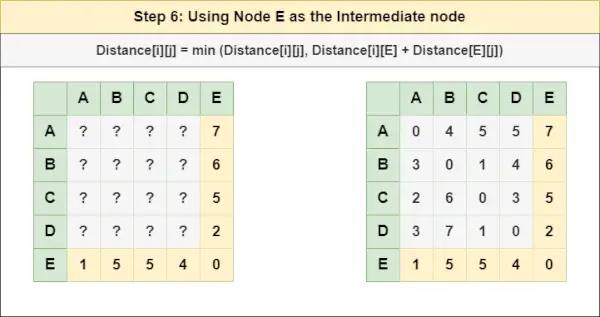
= Відстань[i][j] = мінімум (Відстань[i][j], Відстань[i][ Д ] + Відстань[ Д ][j])Крок 6 : Лікувати вузол І як проміжний вузол і обчислити відстань [][] для кожної пари вузлів {i,j} за формулою:
= Відстань[i][j] = мінімум (Відстань[i][j], (Відстань від i до І ) + (Відстань від І до j))
= Відстань[i][j] = мінімум (Відстань[i][j], Відстань[i][ І ] + Відстань[ І ][j])Крок 7 : Оскільки всі вузли розглядалися як проміжні вузли, тепер ми можемо повернути оновлену матрицю Distance[][] як нашу матрицю відповідей.
Нижче наведено реалізацію вищезазначеного підходу:
C++ // C++ Program for Floyd Warshall Algorithm #include using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Перед початком ітерації ми маємо найкоротші відстані між усіма парами вершин, так що найкоротші відстані розглядають лише вершини в наборі {0, 1, 2, .. k-1} як проміжні вершини. ----> Після закінчення ітерації вершина №. k додається до набору проміжних вершин, і набір стає {0, 1, 2, .. k} */ для (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path from // i to j, then update the value of // dist[i][j] if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Надрукувати матрицю найкоротшої відстані printSolution(dist); } /* Допоміжна функція для друку рішення */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest ' 'distances' ' between every pair of vertices
'; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] == INF) cout << 'INF' << ' '; else cout << dist[i][j] << ' '; } cout << endl; } } // Driver's code int main() { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } }; // Виклик функції floydWarshall(graph); повернути 0; } // Цей код створено Mythri J L> C // C Program for Floyd Warshall Algorithm #include // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value. This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Перед початком ітерації ми маємо найкоротші відстані між усіма парами вершин, так що найкоротші відстані розглядають лише вершини в наборі {0, 1, 2, .. k-1} як проміжні вершини. ----> Після закінчення ітерації вершина №. k додається до набору проміжних вершин, і набір стає {0, 1, 2, .. k} */ для (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path from // i to j, then update the value of // dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Print the shortest distance matrix printSolution(dist); } /* A utility function to print solution */ void printSolution(int dist[][V]) { printf( 'The following matrix shows the shortest distances' ' between every pair of vertices
'); for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] == INF) printf('%7s', 'INF'); else printf('%7d', dist[i][j]); } printf('
'); } } // driver's code int main() { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } }; // Виклик функції floydWarshall(graph); повернути 0; }> Java // Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath { final static int INF = 99999, V = 4; void floydWarshall(int dist[][]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Перед початком ітерації ми маємо найкоротші відстані між усіма парами вершин, так що найкоротші відстані розглядають лише вершини в наборі {0, 1, 2, .. k-1} як проміжні вершини. ----> Після закінчення ітерації вершина №. k додається до набору проміжних вершин, і набір стає {0, 1, 2, .. k} */ для (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path // from i to j, then update the value of // dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Print the shortest distance matrix printSolution(dist); } void printSolution(int dist[][]) { System.out.println( 'The following matrix shows the shortest ' + 'distances between every pair of vertices'); for (int i = 0; i < V; ++i) { for (int j = 0; j < V; ++j) { if (dist[i][j] == INF) System.out.print('INF '); else System.out.print(dist[i][j] + ' '); } System.out.println(); } } // Driver's code public static void main(String[] args) { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1}, { INF, INF, INF, 0 } }; AllPairShortestPath a = new AllPairShortestPath(); // Виклик функції a.floydWarshall(graph); } } // Надано Aakash Hasija> Python3 # Python3 Program for Floyd Warshall Algorithm # Number of vertices in the graph V = 4 # Define infinity as the large # enough value. This value will be # used for vertices not connected to each other INF = 99999 # Solves all pair shortest path # via Floyd Warshall Algorithm def floydWarshall(graph): ''' dist[][] will be the output matrix that will finally have the shortest distances between every pair of vertices ''' ''' initializing the solution matrix same as input graph matrix OR we can say that the initial values of shortest distances are based on shortest paths considering no intermediate vertices ''' dist = list(map(lambda i: list(map(lambda j: j, i)), graph)) ''' Add all vertices one by one to the set of intermediate vertices. --->Перед початком ітерації ми маємо найкоротші відстані між усіма парами вершин, так що найкоротші відстані розглядають лише вершини в наборі {0, 1, 2, .. k-1} як проміжні вершини. ----> Після закінчення ітерації вершина №. k додається до набору проміжних вершин, і набір стає {0, 1, 2, .. k} ''' для k в діапазоні (V): # вибрати всі вершини як джерело одну за одною для i в range(V): # Вибрати всі вершини як призначення для # вибраного вище джерела для j у діапазоні (V): # Якщо вершина k знаходиться на найкоротшому шляху від # i до j, тоді оновіть значення dist[i][ j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Допоміжна функція для друку рішення def printSolution (dist): print('Наступна матриця показує найкоротші відстані між кожною парою вершин') для i в діапазоні (V): для j в діапазоні (V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d ' % (dist[i][j]), end=' ') if j == V-1: print() # Код драйвера if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 ''' графік = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Виклик функції floydWarshall(graph) # Цей код створено Mythri J L> C# // C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath { readonly static int INF = 99999, V = 4; void floydWarshall(int[, ] graph) { int[, ] dist = new int[V, V]; int i, j, k; // Initialize the solution matrix // same as input graph matrix // Or we can say the initial // values of shortest distances // are based on shortest paths // considering no intermediate // vertex for (i = 0; i < V; i++) { for (j = 0; j < V; j++) { dist[i, j] = graph[i, j]; } } /* Add all vertices one by one to the set of intermediate vertices. --->Перед початком ітерації ми маємо найкоротші відстані між усіма парами вершин, так що найкоротші відстані розглядають лише вершини в наборі {0, 1, 2, .. k-1} як проміжні вершини. ---> Після закінчення ітерації вершина №. k додається до набору проміжних вершин, і набір стає {0, 1, 2, .. k} */ для (k = 0; k< V; k++) { // Pick all vertices as source // one by one for (i = 0; i < V; i++) { // Pick all vertices as destination // for the above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest // path from i to j, then update // the value of dist[i][j] if (dist[i, k] + dist[k, j] < dist[i, j]) { dist[i, j] = dist[i, k] + dist[k, j]; } } } } // Print the shortest distance matrix printSolution(dist); } void printSolution(int[, ] dist) { Console.WriteLine( 'Following matrix shows the shortest ' + 'distances between every pair of vertices'); for (int i = 0; i < V; ++i) { for (int j = 0; j < V; ++j) { if (dist[i, j] == INF) { Console.Write('INF '); } else { Console.Write(dist[i, j] + ' '); } } Console.WriteLine(); } } // Driver's Code public static void Main(string[] args) { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int[, ] graph = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } }; AllPairShortestPath a = new AllPairShortestPath(); // Виклик функції a.floydWarshall(graph); } } // Цю статтю надав // Abdul Mateen Mohammed> Javascript // A JavaScript program for Floyd Warshall All // Pairs Shortest Path algorithm. var INF = 99999; class AllPairShortestPath { constructor() { this.V = 4; } floydWarshall(graph) { var dist = Array.from(Array(this.V), () =>новий масив(this.V).fill(0)); змінна i, j, k; // Ініціалізація матриці рішення // так само, як матриця вхідного графа // Або ми можемо сказати, що початкові // значення найкоротших відстаней // засновані на найкоротших шляхах // без урахування проміжної // вершини для (i = 0; i< this.V; i++) { for (j = 0; j < this.V; j++) { dist[i][j] = graph[i][j]; } } /* Add all vertices one by one to the set of intermediate vertices. --->Перед початком ітерації ми маємо найкоротші відстані між усіма парами вершин, так що найкоротші відстані розглядають лише вершини в наборі {0, 1, 2, .. k-1} як проміжні вершини. ---> Після закінчення ітерації вершина №. k додається до набору проміжних вершин, і набір стає {0, 1, 2, .. k} */ для (k = 0; k< this.V; k++) { // Pick all vertices as source // one by one for (i = 0; i < this.V; i++) { // Pick all vertices as destination // for the above picked source for (j = 0; j < this.V; j++) { // If vertex k is on the shortest // path from i to j, then update // the value of dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) { dist[i][j] = dist[i][k] + dist[k][j]; } } } } // Print the shortest distance matrix this.printSolution(dist); } printSolution(dist) { document.write( 'Following matrix shows the shortest ' + 'distances between every pair of vertices ' ); for (var i = 0; i < this.V; ++i) { for (var j = 0; j < this.V; ++j) { if (dist[i][j] == INF) { document.write(' INF '); } else { document.write(' ' + dist[i][j] + ' '); } } document.write(' '); } } } // Driver Code /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ змінний графік = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ]; var a = new AllPairShortestPath(); // Друк рішення a.floydWarshall(graph); // Цей код надано rdtaank.> PHP // PHP Program for Floyd Warshall Algorithm // Solves the all-pairs shortest path problem // using Floyd Warshall algorithm function floydWarshall ($graph, $V, $INF) { /* dist[][] will be the output matrix that will finally have the shortest distances between every pair of vertices */ $dist = array(array(0,0,0,0), array(0,0,0,0), array(0,0,0,0), array(0,0,0,0)); /* Initialize the solution matrix same as input graph matrix. Or we can say the initial values of shortest distances are based on shortest paths considering no intermediate vertex. */ for ($i = 0; $i < $V; $i++) for ($j = 0; $j < $V; $j++) $dist[$i][$j] = $graph[$i][$j]; /* Add all vertices one by one to the set of intermediate vertices. --->Перед початком ітерації ми маємо найкоротші відстані між усіма парами вершин, так що найкоротші відстані розглядають лише вершини в наборі {0, 1, 2, .. k-1} як проміжні вершини. ----> Після закінчення ітерації вершина №. k додається до набору проміжних вершин, і набір стає {0, 1, 2, .. k} */ для ($k = 0; $k< $V; $k++) { // Pick all vertices as source one by one for ($i = 0; $i < $V; $i++) { // Pick all vertices as destination // for the above picked source for ($j = 0; $j < $V; $j++) { // If vertex k is on the shortest path from // i to j, then update the value of dist[i][j] if ($dist[$i][$k] + $dist[$k][$j] < $dist[$i][$j]) $dist[$i][$j] = $dist[$i][$k] + $dist[$k][$j]; } } } // Print the shortest distance matrix printSolution($dist, $V, $INF); } /* A utility function to print solution */ function printSolution($dist, $V, $INF) { echo 'The following matrix shows the ' . 'shortest distances between ' . 'every pair of vertices
'; for ($i = 0; $i < $V; $i++) { for ($j = 0; $j < $V; $j++) { if ($dist[$i][$j] == $INF) echo 'INF ' ; else echo $dist[$i][$j], ' '; } echo '
'; } } // Drivers' Code // Number of vertices in the graph $V = 4 ; /* Define Infinite as a large enough value. This value will be used for vertices not connected to each other */ $INF = 99999 ; /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ $graph = array(array(0, 5, $INF, 10), array($INF, 0, 3, $INF), array($ INF, $INF, 0, 1), масив ($INF, $INF, $INF, 0)); // Виклик функції floydWarshall($graph, $V, $INF); // Цей код створено Ryuga ?>> Вихід
The following matrix shows the shortest distances between every pair of vertices 0 5 8 9 INF 0 3 4 INF INF 0 1 INF INF INF 0>
Аналіз складності алгоритму Флойда Уоршолла:
- Часова складність: O(V3), де V — кількість вершин у графі, і ми запускаємо три вкладені цикли розміром V кожен
- Допоміжний простір: O(V2), щоб створити 2-D матрицю для збереження найкоротшої відстані для кожної пари вузлів.
Примітка : Програма вище друкує лише найкоротші відстані. Ми можемо модифікувати рішення для друку найкоротших шляхів, зберігаючи інформацію про попередника в окремій 2D-матриці.
java розділити рядок роздільником
Чому алгоритм Флойда-Варшалла кращий для щільних графів, а не для розріджених?
Щільний граф : граф, у якому кількість ребер значно перевищує кількість вершин.
Розріджений граф : граф, у якому кількість ребер дуже мала.Незалежно від того, скільки ребер є в графі Алгоритм Флойда Воршелла працює для O(V3) разів, тому він найкраще підходить для Щільні графи . У випадку розріджених графів Алгоритм Джонсона підходить більше.
Важливі питання для співбесіди, пов’язані з Флойдом-Воршаллом:
- Як виявити негативний цикл на графіку за допомогою алгоритму Флойда Уоршалла?
- Чим відрізняється алгоритм Флойда-Воршалла від алгоритму Дейкстри?
- Чим відрізняється алгоритм Флойда-Воршалла від алгоритму Беллмана-Форда?
Реальні застосування алгоритму Флойда-Воршалла:
- У комп’ютерних мережах алгоритм можна використовувати для пошуку найкоротшого шляху між усіма парами вузлів у мережі. Це називається як мережева маршрутизація .
- З’єднання польотів В авіаційній промисловості потрібно знайти найкоротший шлях між аеропортами.
- ГІС ( Геоінформаційні системи ) програми часто передбачають аналіз просторових даних, таких як дорожні мережі, щоб знайти найкоротші шляхи між місцями.
- Алгоритм Кліні який є узагальненням floyd warshall, можна використовувати для пошуку регулярного виразу для звичайної мови.