Що таке структура даних:
Структура даних — це сховище, яке використовується для зберігання та організації даних. Це спосіб упорядкування даних на комп’ютері для ефективного доступу та оновлення.
Структура даних використовується не тільки для організації даних. Він також використовується для обробки, отримання та зберігання даних. Майже в кожній розробленій програмі чи системі програмного забезпечення використовуються різні базові та розширені типи структур даних. Тому ми повинні добре знати структури даних.
Структури даних є невід'ємною частиною комп'ютерів, які використовуються для розміщення даних у пам'яті. Вони важливі й відповідають за організацію, обробку, доступ і ефективне зберігання даних. Але це не все. Різні типи структур даних мають свої характеристики, особливості, застосування, переваги та недоліки. Отже, як визначити структуру даних, яка підходить для конкретного завдання? Що означає термін «Структура даних»? Скільки існує типів структур даних і для чого вони використовуються?

Що таке структура даних: типи, класифікації та застосування
Ми допоможемо вам. Ми склали повний список усього, що таке структура даних, типи структур даних, класифікація структур даних, застосування кожної структури даних тощо. У цій статті ми обговоримо кожен аспект кожної структури даних, щоб допомогти вам вибрати найкращу за лічені хвилини.
Зміст
- Що таке структура даних?
- Як структура даних відрізняється від типу даних?
- Класифікація структури даних
- Масиви
- Зв'язаний список
- Стек
- Черга
- дерево
- Графік
- Висновок
Як структура даних відрізняється від типу даних:
Ми вже вивчили структуру даних. Часто трапляється, що люди плутають тип даних і структуру даних. Отже, давайте розглянемо кілька відмінностей між типом даних і структурою даних, щоб було зрозуміло.
| Тип даних | Структура даних |
|---|---|
| Тип даних — це форма змінної, якій можна присвоїти значення. Він визначає, що конкретна змінна призначатиме значення лише даного типу даних. | Структура даних — це сукупність різних видів даних. Усі ці дані можна представити за допомогою об’єкта та використовувати в усій програмі. |
| Він може зберігати значення, але не дані. Тому він не має даних. | Він може зберігати кілька типів даних в одному об’єкті. |
| Реалізація типу даних відома як абстрактна реалізація. зміщення та дисперсія | Реалізація структури даних відома як конкретна реалізація. |
| У випадку типів даних немає тимчасової складності. | В об’єктах структури даних складність у часі відіграє важливу роль. |
| У випадку типів даних значення даних не зберігається, оскільки воно представляє лише тип даних, який можна зберегти. | У той час як у випадку структур даних, дані та їх значення займають місце в основній пам’яті комп’ютера. Крім того, структура даних може містити різні види та типи даних в одному об’єкті. |
| Прикладами типів даних є int, float, double тощо. | Прикладами структури даних є стек, черга, дерево тощо. |
Класифікація структури даних:
Структура даних має багато різних застосувань у нашому повсякденному житті. Існує багато різних структур даних, які використовуються для вирішення різних математичних і логічних задач. Використовуючи структуру даних, можна організувати й обробити дуже велику кількість даних за відносно короткий період. Давайте розглянемо різні структури даних, які використовуються в різних ситуаціях.
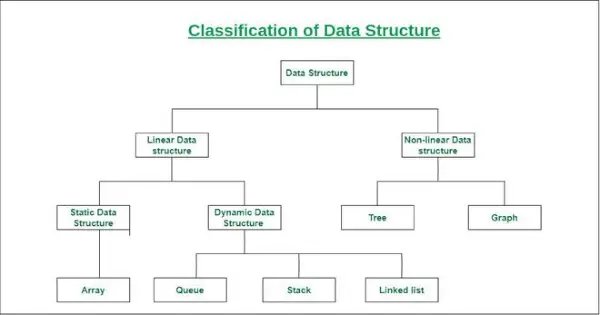
Класифікація структури даних
- Лінійна структура даних: Структура даних, у якій елементи даних розташовані послідовно або лінійно, де кожен елемент приєднаний до своїх попередніх і наступних сусідніх елементів, називається лінійною структурою даних.
Прикладами лінійних структур даних є масив, стек, черга, зв’язаний список тощо.- Статична структура даних: Статична структура даних має фіксований розмір пам'яті. Легше отримати доступ до елементів у статичній структурі даних.
Прикладом такої структури даних є масив. - Динамічна структура даних: У динамічній структурі даних розмір не є фіксованим. Його можна довільно оновлювати під час виконання, що можна вважати ефективним щодо складності пам’яті (простору) коду.
Прикладами такої структури даних є черга, стек тощо.
- Статична структура даних: Статична структура даних має фіксований розмір пам'яті. Легше отримати доступ до елементів у статичній структурі даних.
- Нелінійна структура даних: Структури даних, у яких елементи даних розміщені не послідовно або лінійно, називаються нелінійними структурами даних. У нелінійній структурі даних ми не можемо пройти всі елементи за один прогін.
Прикладами нелінійних структур даних є дерева та графи.
Необхідність структури даних:
Структура даних і синтез алгоритму відносні один до одного. Представлення даних повинно бути легким для розуміння, щоб розробник, а також користувач могли ефективно реалізувати операцію.
Структури даних забезпечують простий спосіб організації, пошуку, керування та зберігання даних.
Ось список потреб у даних.
- Змінити структуру даних легко.
- Це вимагає менше часу.
- Економія пам'яті для зберігання.
- Представлення даних просте.
- Легкий доступ до великої бази даних.
Масиви:
Масив — це лінійна структура даних, набір елементів, що зберігаються в безперервних місцях пам’яті. Ідея полягає в тому, щоб зберігати кілька предметів одного типу разом в одному місці. Це дозволяє обробляти велику кількість даних за відносно короткий період. Перший елемент масиву індексується нижнім індексом 0. У масиві можливі різні операції, як-от пошук, сортування, вставлення, обхід, реверсування та видалення.

Масив
Характеристики масиву:
Масив має різні характеристики, а саме:
- Масиви використовують структуру даних на основі індексу, яка допомагає легко ідентифікувати кожен елемент у масиві за допомогою індексу.
- Якщо користувач хоче зберігати кілька значень одного типу даних, тоді масив можна ефективно використовувати.
- Масив також може обробляти складні структури даних, зберігаючи дані в двовимірному масиві.
- Масив також використовується для реалізації інших структур даних, таких як стеки, черги, купи, хеш-таблиці тощо.
- Процес пошуку в масиві можна виконати дуже легко.
Операції, що виконуються над масивом:
- Ініціалізація : Масив можна ініціалізувати значеннями під час оголошення або пізніше за допомогою оператора присвоєння.
- Доступ до елементів: Доступ до елементів у масиві можна отримати за їх індексом, який починається з 0 і зростає до розміру масиву мінус одиниця.
- Пошук елементів : у масивах можна шукати певний елемент за допомогою алгоритмів лінійного або бінарного пошуку.
- Сортування елементів : Елементи в масиві можна сортувати за зростанням або спаданням за допомогою таких алгоритмів, як спливаюче сортування, сортування вставкою або швидке сортування.
- Вставка елементів: Елементи можна вставляти в масив у певному місці, але ця операція може зайняти багато часу, оскільки вимагає переміщення існуючих елементів у масиві.
- Видалення елементів: Елементи можна видалити з масиву, зсуваючи елементи, які йдуть після нього, щоб заповнити проміжок.
- Елементи оновлення: Елементи в масиві можна оновити або змінити, присвоївши нове значення певному індексу.
- Елементи траверси: Елементи в масиві можна обходити по порядку, відвідуючи кожен елемент один раз.
Це деякі з найпоширеніших операцій, які виконуються над масивами. Використовувані конкретні операції та алгоритми можуть відрізнятися залежно від вимог проблеми та мови програмування, що використовується.
Застосування масиву:
Нижче наведено різні застосування масиву:
- Масив використовується при розв’язуванні матричних задач.
- Записи бази даних також реалізуються масивом.
- Це допомагає реалізувати алгоритм сортування.
- Він також використовується для реалізації інших структур даних, таких як стеки, черги, купи, хеш-таблиці тощо.
- Масив можна використовувати для планування ЦП.
- Може використовуватися як таблиця пошуку в комп’ютерах.
- Масиви можна використовувати в обробці мовлення, де кожен мовний сигнал є масивом.
- Екран комп'ютера також відображається масивом. Тут ми використовуємо багатовимірний масив.
- Масив використовується в багатьох системах управління, таких як бібліотека, студенти, парламент тощо.
- Масив використовується в системі онлайн-бронювання квитків. У цьому масиві відображаються контакти на мобільному телефоні.
- У таких іграх, як онлайн-шахи, де гравець може зберігати свої минулі ходи, а також поточні ходи. Це вказує на натяк на позицію.
- Щоб зберегти зображення в певному розмірі на андроїд, наприклад, 360*1200
Застосування масиву в реальному житті:
- Масив часто використовується для зберігання даних для математичних обчислень.
- Використовується в обробці зображень.
- Він також використовується в управлінні записами.
- Сторінки книги також є реальними прикладами масиву.
- Він також використовується для замовлення коробок.
Хочете почати роботу з масивами? Ви можете спробувати наші підібрані статті та списки для найкращої практики:
- Вступ до структури даних масиву
- 50 основних проблем кодування масивів для співбесід
- Відпрацюйте задачу з масивом на techcodeview.com
Зв'язаний список:
Зв’язаний список — це лінійна структура даних, у якій елементи не зберігаються в безперервних місцях пам’яті. Елементи у зв’язаному списку зв’язуються за допомогою вказівників, як показано на зображенні нижче:
Типи пов'язаних списків:
- Однозв'язний список
- Двозв'язний список
- Круговий пов'язаний список
- Подвійний кільцевий пов’язаний список

Зв'язаний список
Характеристики пов’язаного списку:
Зв’язаний список має різні характеристики, а саме:
java string.format
- Зв’язаний список використовує додаткову пам’ять для зберігання посилань.
- Під час ініціалізації зв’язаного списку немає необхідності знати розмір елементів.
- Зв’язані списки використовуються для реалізації стеків, черг, графів тощо.
- Перший вузол пов’язаного списку називається Головою.
- Наступний покажчик останнього вузла завжди вказує на NULL.
- У пов’язаному списку можна легко вставляти та видаляти.
- Кожен вузол пов’язаного списку складається з покажчика/посилання, яке є адресою наступного вузла.
- Пов’язані списки можуть легко зменшуватися або розширюватися в будь-який момент часу.
Операції, що виконуються над пов’язаним списком:
Зв’язаний список — це лінійна структура даних, де кожен вузол містить значення та посилання на наступний вузол. Ось кілька поширених операцій, які виконуються над пов’язаними списками:
- Ініціалізація: Зв’язаний список можна ініціалізувати шляхом створення головного вузла з посиланням на перший вузол. Кожен наступний вузол містить значення та посилання на наступний вузол.
- Вставка елементів: Елементи можна вставляти в початок, хвіст або в певну позицію зв’язаного списку.
- Видалення елементів : елементи можна видалити зі зв’язаного списку, оновивши посилання попереднього вузла на наступний вузол, фактично видаливши поточний вузол зі списку.
- Пошук елементів : у пов’язаних списках можна шукати певний елемент, починаючи з головного вузла та дотримуючись посилань на наступні вузли, доки не буде знайдено потрібний елемент.
- Оновлення елементів : Елементи у зв’язаному списку можна оновлювати, змінюючи значення певного вузла.
- Елементи траверси: Елементи у зв’язаному списку можна обійти, починаючи з головного вузла та дотримуючись посилань на наступні вузли, доки не буде досягнуто кінець списку.
- Скасування пов’язаного списку : зв’язаний список можна змінити, оновивши посилання кожного вузла так, щоб вони вказували на попередній вузол замість наступного.
Це деякі з найпоширеніших операцій, які виконуються над пов’язаними списками. Використовувані конкретні операції та алгоритми можуть відрізнятися залежно від вимог проблеми та мови програмування, що використовується.
Програми пов’язаного списку:
Нижче наведено різні застосування пов’язаних списків:
- Зв’язані списки використовуються для реалізації стеків, черг, графів тощо.
- Зв’язані списки використовуються для виконання арифметичних операцій над довгими цілими числами.
- Використовується для представлення розріджених матриць.
- Він використовується для пов’язаного розміщення файлів.
- Це допомагає в управлінні пам'яттю.
- Він використовується в представленні поліноміальної маніпуляції, де кожен поліноміальний термін представляє вузол у зв’язаному списку.
- Зв’язані списки використовуються для відображення контейнерів зображень. Користувачі можуть переглядати минулі, поточні та наступні зображення.
- Вони використовуються для зберігання історії відвіданої сторінки.
- Вони використовуються для виконання операцій скасування.
- Пов’язані використовуються в розробці програмного забезпечення, де вони вказують на правильний синтаксис тегу.
- Зв’язані списки використовуються для відображення стрічок соціальних мереж.
Реальні програми пов’язаного списку:
- Зв’язаний список використовується в плануванні Round-Robin, щоб відстежувати хід у багатокористувацьких іграх.
- Він використовується у програмі перегляду зображень. Попереднє та наступне зображення пов’язані, тому до них можна отримати доступ за допомогою кнопок «попередній» і «наступний».
- У музичному списку відтворення пісні пов’язані з попередньою та наступною піснями.
Хочете почати роботу зі зв’язаного списку? Ви можете спробувати наші підібрані статті та списки для найкращої практики:
- Вступ до структури даних пов’язаного списку
- 20 найпопулярніших питань для співбесіди зі зв’язаним списком
- Відпрацюйте задачу пов’язаного списку на techcodeview.com
Стек:
Стек — це лінійна структура даних, яка дотримується певного порядку виконання операцій. Порядок є LIFO (останній прийшов, перший вийшов) . Введення та отримання даних можливе лише з одного боку. Введення та отримання даних також називається операцією push and pop у стеку. У стеку можливі різні операції, наприклад перевертання стека за допомогою рекурсії, сортування, видалення середнього елемента стека тощо.

Стек
Характеристики стека:
Стек має різні характеристики, які є такими:
- Стек використовується в багатьох різних алгоритмах, таких як Ханойська вежа, обхід дерева, рекурсія тощо.
- Стек реалізується через масив або зв'язаний список.
- Це слідує за операцією «Останній прийшов – перший вийшов», тобто елемент, який вставлено першим, з’явиться останнім і навпаки.
- Вставка та видалення виконуються з одного кінця, тобто з вершини стека.
- У стеку, якщо виділений простір для стека заповнений, і все одно хтось намагається додати більше елементів, це призведе до переповнення стеку.
Застосування Stack:
Нижче наведено різні програми Stack:
- Структура стекових даних використовується для обчислення та перетворення арифметичних виразів.
- Використовується для перевірки круглих дужок.
- Під час реверсування рядка також використовується стек.
- Стек використовується в управлінні пам'яттю.
- Він також використовується для обробки викликів функцій.
- Стек використовується для перетворення виразів з інфіксних у постфіксні.
- Стек використовується для виконання операцій скасування та повторення в текстових процесорах.
- Стек використовується у віртуальних машинах, таких як JVM.
- Стек використовується в медіаплеєрах. Корисно для відтворення наступної та попередньої пісні.
- Стек використовується в операціях рекурсії.
Операція, виконана в стеку;
Стек — це лінійна структура даних, яка реалізує принцип «останній прийшов першим вийшов» (LIFO). Ось кілька типових операцій, які виконуються над стеками:
- Поштовх : Елементи можна помістити на вершину стека, додаючи новий елемент на вершину стека.
- Поп : верхній елемент можна вилучити зі стеку, виконавши операцію висунення, фактично видаливши останній елемент, який було вставлено в стек.
- Подивіться: Верхній елемент можна перевірити, не виймаючи його зі стека, за допомогою операції перегляду.
- Пусто : Можна перевірити, чи стек порожній.
- Розмір : кількість елементів у стеку можна визначити за допомогою операції розміру.
Це деякі з найпоширеніших операцій, які виконуються над стеками. Використовувані конкретні операції та алгоритми можуть відрізнятися залежно від вимог проблеми та мови програмування, що використовується. Стеки зазвичай використовуються в таких програмах, як обчислення виразів, реалізація стеків викликів функцій у комп’ютерних програмах та багатьох інших.
Застосування Stack у реальному житті:
- Реальним прикладом стопки є шар тарілок, розташованих одна над одною. Коли ви знімаєте тарілку з купи, ви можете взяти тарілку на вершину купи. Але це саме та тарілка, яку нещодавно додали до купи. Якщо вам потрібна тарілка внизу купи, ви повинні видалити всі тарілки зверху, щоб дістатися до неї.
- Браузери використовують стекові структури даних для відстеження відвіданих раніше сайтів.
- Журнал викликів у мобільному телефоні також використовує стекову структуру даних.
Хочете почати роботу зі Stack? Ви можете спробувати наші підібрані статті та списки для найкращої практики:
життєвий цикл розробки програмного забезпечення
- Практична задача зі стеком на techcodeview.com
Черга:
Черга — це лінійна структура даних, яка відповідає певному порядку виконання операцій. Порядок є Першим увійшов, першим вийшов (FIFO) тобто першим буде доступ до елемента даних, збереженого першим. У цьому випадку введення та отримання даних не виконується лише з одного боку. Прикладом черги є будь-яка черга споживачів для ресурсу, де споживач, який прийшов першим, обслуговується першим. З чергою виконуються різні операції, як-от реверсування черги (з або без використання рекурсії), реверсування перших K елементів черги тощо. Кілька основних операцій, які виконуються в черзі, це введення в чергу, вилучення з черги, передня, задня тощо.
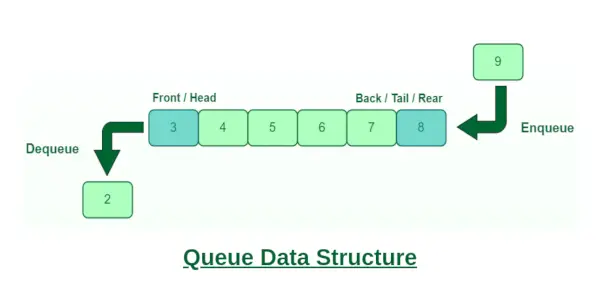
Черга
Характеристики черги:
Черга має різні характеристики, а саме:
- Черга є структурою FIFO (першим прийшов, першим вийшов).
- Щоб видалити останній елемент черги, потрібно видалити всі елементи, вставлені перед новим елементом у черзі.
- Черга — це впорядкований список елементів подібних типів даних.
Застосування черги:
Нижче наведено різні програми Queue:
- Черга використовується для обробки трафіку веб-сайту.
- Це допомагає підтримувати список відтворення в медіаплеєрах.
- Черга використовується в операційних системах для обробки переривань.
- Це допомагає обслуговувати запити на одному спільному ресурсі, як-от принтер, планування завдань ЦП тощо.
- Він використовується в асинхронній передачі даних, наприклад. канали, файловий IO та сокети.
- Черги використовуються для планування завдань в операційній системі.
- У соціальних мережах для завантаження кількох фотографій або відео використовується черга.
- Для надсилання електронного листа використовується структура даних черги.
- Для обробки трафіку веб-сайту одночасно використовуються черги.
- В операційній системі Windows для перемикання кількох програм.
Операція, виконана в черзі:
Черга — це лінійна структура даних, яка реалізує принцип «першим прийшов — першим вийшов» (FIFO). Ось кілька поширених операцій, які виконуються над чергами:
- Поставте в чергу : елементи можна додавати до кінця черги, додаючи новий елемент у кінець черги.
- Відповідно : передній елемент можна видалити з черги, виконавши операцію вилучення з черги, фактично видаливши перший елемент, який було додано до черги.
- Peek : передній елемент можна перевірити, не видаляючи його з черги за допомогою операції перегляду.
- Пусто : Можна перевірити, чи черга порожня.
- Розмір : кількість елементів у черзі можна визначити за допомогою операції розміру.
Це деякі з найпоширеніших операцій, які виконуються над чергами. Використовувані конкретні операції та алгоритми можуть відрізнятися залежно від вимог проблеми та мови програмування, що використовується. Черги зазвичай використовуються в таких програмах, як планування завдань, керування зв’язком між процесами та багато інших.
Застосування черги в реальному житті:
- Реальним прикладом черги є односмугова дорога з одностороннім рухом, де транспортний засіб, який в’їжджає першим, виїжджає першим.
- Більш реальний приклад можна побачити в черзі біля квиткових кас.
- Черга до каси в магазині також є прикладом черги.
- Люди на ескалаторі
Хочете почати роботу з чергою? Ви можете спробувати наші підібрані статті та списки для найкращої практики:
- Відпрацюйте проблему черги на techcodeview.com
дерево:
Дерево — це нелінійна ієрархічна структура даних, де елементи впорядковані у вигляді дерева. У дереві найвищий вузол називається кореневим вузлом. Кожен вузол містить деякі дані, і дані можуть бути будь-якого типу. Він складається з центрального вузла, структурних вузлів і підвузлів, які з’єднані ребрами. Різні деревовидні структури даних забезпечують швидший і легший доступ до даних, оскільки це нелінійна структура даних. Дерево має різні термінології, наприклад вузол, корінь, ребро, висота дерева, ступінь дерева тощо.
Існують різні види деревоподібних
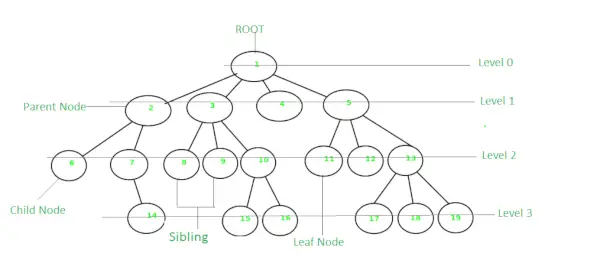
дерево
Характеристики дерева:
Дерево має різні характеристики, а саме:
- Дерево також відоме як рекурсивна структура даних.
- У дереві висоту кореня можна визначити як найдовший шлях від кореневого вузла до листкового вузла.
- У дереві також можна обчислити глибину від вершини до будь-якого вузла. Кореневий вузол має глибину 0.
Застосування дерева:
Нижче наведено різні програми Tree:
- Купа — це деревоподібна структура даних, яка реалізована за допомогою масивів і використовується для реалізації пріоритетних черг.
- B-Tree і B+ Tree використовуються для реалізації індексації в базах даних.
- Синтаксичне дерево допомагає сканувати, розбирати, генерувати код і оцінювати арифметичні вирази в компіляторі.
- K-D Tree — це дерево поділу простору, яке використовується для організації точок у K-вимірному просторі.
- Spanning Trees використовуються в маршрутизаторах комп'ютерних мереж.
Операція, виконана на дереві:
Дерево — це нелінійна структура даних, яка складається з вузлів, з’єднаних ребрами. Ось кілька поширених операцій, які виконуються з деревами:
- Вставка : до дерева можна додати нові вузли, щоб створити нову гілку або збільшити висоту дерева.
- Видалення : Вузли можна видалити з дерева, оновивши посилання батьківського вузла, щоб видалити посилання на поточний вузол.
- Пошук : елементи можна шукати в дереві, починаючи з кореневого вузла та обходячи дерево на основі значення поточного вузла, доки не буде знайдено потрібний вузол.
- Обхід : елементи в дереві можна обходити декількома різними способами, включно з обходом у порядку, попередньому порядку та після порядку.
- Висота : Висоту дерева можна визначити, підрахувавши кількість ребер від кореневого вузла до найдальшого вузла листа.
- Глибина : Глибину вузла можна визначити, підрахувавши кількість ребер від кореневого вузла до поточного вузла.
- Балансування : Дерево можна збалансувати, щоб забезпечити мінімізовану висоту дерева та максимально рівномірний розподіл вузлів.
Це одні з найпоширеніших операцій, які виконуються на деревах. Використовувані конкретні операції та алгоритми можуть відрізнятися залежно від вимог проблеми та мови програмування, що використовується. Дерева зазвичай використовуються в таких програмах, як пошук, сортування та зберігання ієрархічних даних.
Застосування дерева в реальному житті:
- У реальному житті структура даних дерева допомагає в розробці гри.
- Це також допомагає в індексації в базах даних.
- Дерево рішень — це ефективний інструмент машинного навчання, який зазвичай використовується в аналізі рішень. Він має структуру, схожу на блок-схему, яка допомагає зрозуміти дані.
- Сервер доменних імен також використовує деревовидну структуру даних.
- Найпоширенішим випадком використання дерева є будь-який сайт соціальної мережі.
Хочете почати роботу з Tree? Ви можете спробувати наші підібрані статті та списки для найкращої практики:
- 50 найпопулярніших питань для інтерв’ю про дерево
- Практична задача Tree на techcodeview.com
Графік:
Граф — це нелінійна структура даних, яка складається з вершин (або вузлів) і ребер. Він складається з кінцевого набору вершин і набору ребер, які з’єднують пару вузлів. Граф використовується для вирішення найскладніших і складних задач програмування. Він має різні термінології, як-от Шлях, Ступінь, Сусідні вершини, З’єднані компоненти тощо.
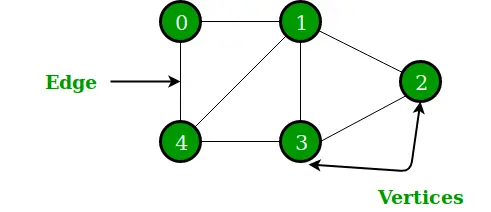
Графік
Характеристики графіка:
Графік має різні характеристики, а саме:
- Максимальна відстань від вершини до всіх інших вершин вважається ексцентриситетом цієї вершини.
- Вершина з мінімальним ексцентриситетом вважається центральною точкою графа.
- Мінімальне значення ексцентриситету з усіх вершин вважається радіусом зв'язного графа.
Застосування Graph:
Нижче наведено різні варіанти застосування Graphs:
- Графік використовується для представлення потоку обчислень.
- Використовується при моделюванні графів.
- Операційна система використовує Resource Allocation Graph.
- Також використовується у Всесвітній павутині, де веб-сторінки представляють вузли.
Операція, виконана на графіку:
Граф — це нелінійна структура даних, що складається з вузлів і ребер. Ось кілька поширених операцій, які виконуються на графіках:
- Додати вершину: Нові вершини можна додавати до графа, щоб представляти новий вузол.
- Додати край: Ребра можна додавати між вершинами, щоб представити зв’язок між вузлами.
- Видалити Vertex : Вершини можна видалити з графа, оновивши посилання на суміжні вершини, щоб видалити посилання на поточну вершину.
- Видаліть Edge : Ребра можна видалити, оновивши посилання на суміжні вершини, щоб видалити посилання на поточне ребро.
- Пошук у глибину (DFS) : Гра можна обійти за допомогою пошуку в глибину, відвідуючи вершини в глибину.
- Б пошук спочатку читання (BFS): Граф можна обійти за допомогою пошуку вшир, відвідуючи вершини в ширину.
- Найкоротший шлях: Найкоротший шлях між двома вершинами можна визначити за допомогою таких алгоритмів, як алгоритм Дейкстри або алгоритм A*.
- Підключені компоненти : З’єднані компоненти графа можна визначити, знайшовши набори вершин, які з’єднані одна з одною, але не з’єднані з іншими вершинами в графі.
- Виявлення циклу : Цикли в графі можна виявити шляхом перевірки задніх ребер під час пошуку в глибину.
Це одні з найпоширеніших операцій, які виконуються над графіками. Використовувані конкретні операції та алгоритми можуть відрізнятися залежно від вимог проблеми та мови програмування, що використовується. Графіки зазвичай використовуються в таких програмах, як комп’ютерні мережі, соціальні мережі та проблеми маршрутизації.
Застосування Graph у реальному житті:
- Одним із найпоширеніших реальних прикладів графа є Карти Google, де міста розташовані як вершини, а шляхи, що з’єднують ці вершини, розташовані як ребра графа.
- Соціальна мережа також є реальним прикладом графіка, де кожна особа в мережі є вузлом, а всі їхні друзі в мережі є краями графіка.
- Граф також використовується для вивчення молекул у фізиці та хімії.
Хочете почати роботу з Graph? Ви можете спробувати наші підібрані статті та списки для найкращої практики:
strsep
- Вступ до структури даних графа
- 50 найпопулярніших питань інтерв’ю Graph
- Відпрацюйте графічну задачу на techcodeview.com
Переваги структури даних:
- Покращена організація даних і ефективність зберігання.
- Швидший пошук і обробка даних.
- Полегшує розробку алгоритмів для вирішення складних задач.
- Полегшує завдання оновлення та підтримки даних.
- Забезпечує краще розуміння зв’язків між елементами даних.
Недолік структури даних:
- Збільшення накладних витрат на обчислення та пам’ять.
- Труднощі в проектуванні та реалізації складних структур даних.
- Обмежена масштабованість і гнучкість.
- Складність у налагодженні та тестуванні.
- Труднощі зі зміною існуючих структур даних.
Посилання:
Структури даних можна знайти в різних підручниках з інформатики та інтернет-ресурсах. Деякі популярні тексти включають:
- Вступ до алгоритмів Томаса Х. Кормена, Чарльза Е. Лейзерсона, Рональда Л. Ріввеста та Кліффорда Стайна.
- Структури даних і аналіз алгоритмів у Java, Марк Аллен Вайс.
- Посібник з розробки алгоритмів Стівена С. Скіени.
- Онлайн-ресурси, такі як Coursera, Udemy та Khan Academy, також пропонують курси зі структур даних і алгоритмів.
Висновок
Хоча це найбільш відомі та використовувані структури даних, існують також деякі інші форми структур даних, які використовуються в інформатиці, такі як структури даних на основі політики тощо. Але незалежно від того, яку структуру даних ви виберете, кожна з них має свої переваги та недоліки, без знання яких вибір неправильного типу структури даних може коштувати дуже дорого. Тому дуже важливо зрозуміти потреби ситуації, а потім вирішити, яка структура даних найкраще підходить для роботи.
