Складні відсотки – це відсотки, які нараховуються на суму позики чи депозиту, в якій відсотки нараховуються як на основну суму, так і на попередні отримані відсотки.

Загальна різниця між складними і простими відсотками полягає в тому, що в складні відсотки , відсотки розраховуються як на основну суму, так і на попередньо зароблені відсотки, тоді як прості відсотки залежать лише від основної суми інвестованого боргу.

Зміст

• Що таке складні відсотки?
• Формула складних відсотків
• Як розрахувати складні відсотки?
• Формула складних відсотків – виведення
• Піврічна формула складних відсотків
• Формула квартальних складних відсотків
• Формула місячних складних відсотків
• Формула щоденних складних відсотків
• Формула періодичної ставки компаундування
• Правило 72
• Складні відсотки за послідовні роки
• Формула постійного нарахування відсотків
• Деякі інші застосування складних відсотків
• Різниця між складними відсотками та простими відсотками
• Приклади складних відсотків
• Складні відсотки – практичні запитання

Що таке складні відсотки?

Складні відсотки — це відсотки на основну суму, а також відсотки, отримані на основну суму. Слово Compound Interest складається з двох слів Складний, що означає, що складається з двох або більше, а відсоток означає гроші, зароблені на позичанні суми. Таким чином, складні відсотки — це гроші, зароблені на кредитуванні, і вони складаються з двох видів відсотків, а саме:

• Відсотки на основну суму

• Відсотки на відсотки, зароблені на основну суму за період

Визначення складних відсотків

Складні відсотки це відсотки, нараховані на основну суму боргу та відсотки, отримані раніше. Позначається C.I. Це дуже корисно для інвестицій та погашення кредиту. Він також відомий як відсотки на відсотки.

колесо прокрутки не працює

Складні відсотки дуже корисний у банківському та фінансовому секторах, а також корисний в інших секторах. Деякі з його використання:

• Зростання чисельності населення країни
• Вартість інвестицій за певний період часу.
• Для виявлення завищених витрат і амортизованої вартості будь-якого товару.
• Для прогнозування зростання будь-якої установи чи країни.

Складні відсотки (C.I) = Сума – Основна сума

Формула складних відсотків

Складні відсотки розраховується після підрахунку загальної суми за період часу на основі процентної ставки та початкової основної суми. Для початкової основної суми P, процентної ставки на рік r, періоду часу t у роках, частоти нарахування відсотків щорічно n, формула для розрахунку CI виглядає так:

CI = P(1 + r/100) ^п – С

Наведену вище формулу для розрахунку складних відсотків додано у форму зображення нижче:

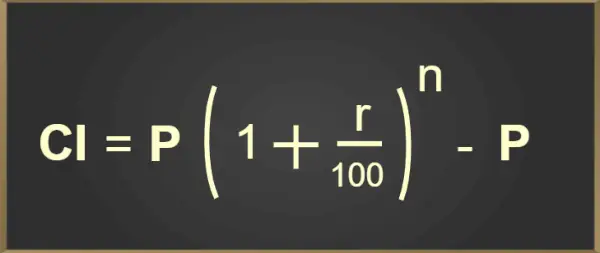
Формула складних відсотків

Де,

• P = Основний
• r = процентна ставка
• n = кількість разів нарахування відсотків на рік
• t = Час (у роках)

Ми можемо записати формулу складних відсотків так:

Складні відсотки = A – P

Де,

• А = Загальна сума грошей після складення
• P = Початкова основна сума

Складні відсотки = P(1 + r/n) ^nt -П

Де,

• P = Початкова основна сума
• r = річна процентна ставка
• n = кількість разів нарахування відсотків
• t = кількість років

Складні відсотки можна розраховувати щороку, півроку, кварталу, місяця, дня тощо відповідно до вимог.

Як розрахувати складні відсотки?

Складні відсотки це відсотки, сплачені як на основну суму, так і на накопичені відсотки. Відсотки, отримані за кожний інтервал, додаються до початкової основної суми, таким чином основна сума продовжує зростати.

Використовуйте наступні методи, щоб знайти складні відсотки.

Крок 1: Вказано примітку, основну суму, ставку та період часу

Крок 2. Обчисліть суму за формулою A = P(1 + r/100) ^п

Крок 3: Знайдіть складні відсотки за формулою CI = Сума – Основна сума

Через регулярні проміжки часу накопичені відсотки дорівнюють поточній основній сумі, а потім відсотки розраховується на нового принципала . Нова основна сума дорівнює сумі початкової основної суми та відсотків, накопичених до цього часу.

Складний відсоток = відсоток на основну суму + відсоток на основну суму (з другого року і далі)

Складні відсотки розраховуються через регулярні проміжки часу, як-от щорічно (щороку), півроку, щокварталу, щомісяця, тощо; Схоже на те, що реінвестування процентного доходу від інвестиції змушує гроші рости швидше з часом! Це саме те, що складні відсотки роблять з грошима. Банки або будь-які фінансові організації розраховують суму лише на основі складних відсотків.

Формула складних відсотків – виведення

Формула складних відсотків — це потужний інструмент, який використовується у фінансах для розрахунку відсотків, отриманих або сплачених на початкову основну суму, який включає як початкову основну суму, так і відсотки, накопичені за попередні періоди. Формула складних відсотків визначається так:

Де,

• A — майбутня вартість інвестицій або позики, включаючи відсотки
• P — основна сума (початкові інвестиції або сума кредиту)
• r – річна процентна ставка (у десятковому вигляді)
• n – кількість нарахувань відсотків на рік
• t – це час, на який інвестовано або позичено гроші, у роках

Проста формула відсотків

Прості відсотки нараховуються тільки на основну суму. Його можна представити формулою ,

Формула складних відсотків із безперервним нарахуванням відсотків

Коли відсотки нараховуються безперервно (нескінченно багато разів на рік), формула складних відсотків виводиться за формулою безперервного нарахування:

Де,

• e – число Ейлера (приблизно 2,71828)
• P — основна сума
• r — річна відсоткова ставка
• t – час у роках

Загальна формула складних відсотків

Щоб отримати загальну формулу складних відсотків, розглянемо нарахування відсотків n разів на рік.

Якщо P нараховується n разів на рік із річною відсотковою ставкою r, відсотки r діляться на n і застосовуються n разів на рік. Отже, через t років формула набуває вигляду:

Де,

• представляє процентну ставку за період нарахування.
• nt – загальна кількість періодів компаундування за t років.

Це Формула ілюструє, як початкова основна сума зростає з часом, коли відсотки нараховуються через регулярні проміжки часу . Коли n наближається до нескінченності (тобто безперервне компаундування), формула збігається до формули безперервного компаундування .

Підсумовуючи, формула складних відсотків є результатом безперервної формули компаундування, адаптованої для окремих періодів компаундування на рік. Це дозволяє розрахувати майбутню вартість інвестиції чи позики, враховуючи нараховані відсотки через регулярні проміжки часу.

Піврічна формула складних відсотків

Нехай основна сума інвестованого боргу дорівнює P, а відсоткова ставка R % річних, яка нараховується кожні півроку протягом «t» років

як складається кожні півроку, довіритель буде змінено в кінці 6 місяців, і відсотки, зароблені до того часу, будуть додані до основної суми, і тоді це стане новою основною сумою. Аналогічно розраховується остаточна сума.

Ми знаємо,

ставка = R% на рік, складена на півроку

швидкість = (R/2) %

btree і b дерево

час становить t років, ми знаємо, що минуло t років 2т півроку.

тепер,

A = P (1 + R/200) ^2т

CI = A – P

Формула квартальних складних відсотків

Нехай основна сума вкладених коштів дорівнює P, а відсоткова ставка R % річних, яка нараховується щокварталу протягом t років.

як вона складається щоквартально, основна сума буде змінена в кінці 3 місяців, і відсотки, отримані до того моменту, будуть додані до основної суми, і тоді це стане новою основною сумою. Аналогічно розраховується остаточна сума.

ми знаємо,

ставка = R% річних, що складається щоквартально

швидкість = (R/4)%

час становить t років, ми знаємо, що минуло t років 4т чверті.

тепер,

A = P(1 + R/400) ^4т

CI = A – P

перевірити: Квартальна формула складних відсотків

Формула місячних складних відсотків

Якщо відсотки нараховуються щомісяця, кількість нарахувань становитиме 12 разів, а відсотки кожного місяця становитимуть 1/12 річних складних відсотків. Отже, формула місячних складних відсотків наводиться як

A = P[1 + (R/1200)] ^12т

CI = A – P

перевірити: Формула місячних складних відсотків

Формула щоденних складних відсотків

Якщо відсотки нараховуються щодня, тоді.

Нова відсоткова ставка становитиме R/365 %

n = 365

Отже, щоденна формула складного відсотка подається як

A = P[1 + (R/36500)] ^365т

CI = A – P

Формула періодичної ставки компаундування

Загальна сума, включаючи основну суму P та нараховані відсотки CI, визначається за формулою:

A = P[1 + (r/n)] ^nt

де,

• P = Основний
• A = Остаточна сума
• r = річна процентна ставка
• n = кількість разів нарахування відсотків
• t = Час (у роках)

Отже, складні відсотки це:

CI = A – P

Правило 72

Правило 72 — це формула, яка використовується для оцінки того, через скільки років наші гроші подвоюються, якщо їх щорічно складати. для приклад , якщо наші гроші вкладені в r % щороку, то потрібно 72 роки, щоб наші гроші подвоїлися.

Цей розрахунок також корисний для розрахунку завищеної вартості наших грошей, тобто це показує, через скільки років вартість нашого активу зменшується вдвічі, якщо він щорічно амортизується.

Формула правила 72

Наступна формула використовується для приблизного розрахунку кількості років, протягом яких наші інвестиції подвоюються.

N = 72 / р

де,

• Н це приблизна кількість років, коли наші гроші подвоюються
• r це ставка, за якою наші гроші нараховуються щорічно

Приклад правила 72

Припустімо, що Кабір інвестував 10 00 000 рупій у борговий фонд, який дає 8% прибутку. Знайдіть, через скільки років його гроші подвоюються, якщо вони складаються щорічно.

Використовуючи наведену вище формулу: N = 72/8 = 9 років

Таким чином, потрібно 9 років, щоб гроші Кабіра подвоїлися.

Складні відсотки за послідовні роки

Якщо ми маємо однакову суму й однакову процентну ставку. C.I. окремого року завжди більше, ніж C.I попереднього року. (ДІ 3-го року більше, ніж ДІ 2-го року). Різниця між CI за будь-які два послідовні роки є відсотками за один рік від C.I попереднього року.

C.I 3-го року – C.I 2-го року = C.I 2-го року × r × 1/100

Різниця між сумами будь-яких двох послідовних років є відсотками за один рік від суми попереднього року.

Сума 3-го року – Сума 2-го року = Сума 2-го року × r × 1/100

Ключові результати

Коли ми маємо однакову суму та однакову ставку ,

C.I за n-й рік = C.I за (n – 1)-й рік + відсотки за один рік на C.I за (n – 1)-й рік

Формула постійного нарахування відсотків

Формула безперервного компаундування використовується у фінансах для розрахунку остаточної вартості інвестицій, які піддаються безперервному компаундуванню протягом різних періодів і вартість яких додається з часом. Формула безперервного компаундування подана як

Кінцева вартість = поточна вартість × e ^{кімнатна температура}

де,

• r — процентна ставка
• t це час

Вивчайте більше, Формула безперервного компаундування

Деякі інші застосування складних відсотків

Зростання: Це в основному використовується для зростання, якщо галузі пов’язані.

Виробництво через n років = початкове виробництво × (1 + r/100) ^п

Амортизація: коли вартість продукту знецінюється на r% щороку, його вартість через n років дорівнює

Поточне значення × (1 + r/100) ^п

Проблеми населення: коли населення міста чи села збільшується з певною швидкістю на рік.

Населення через n років = поточне населення × (1 + r/100) ^п

Різниця між складними відсотками та простими відсотками

Про різницю між складними відсотками та простими відсотками можна дізнатися нижче в цій статті

Приклади складних відсотків

Деякі приклади формул складних відсотків:

Приклад 1: Знайдіть складний відсоток, якщо основна сума = 6000 рупій, ставка = 10% річних і час = 2 роки.

рішення:

Відсотки за перший рік = (6000 × 10 × 1)/100 = 600

Сума на кінець першого року = 6000 + 600 = 6600

Відсотки за другий рік = (6600 × 10 × 1) / 100 = 660

пружинний каркас

Сума наприкінці другого року = 6600 + 660 = 7260

Складні відсотки = 7260 – 6000 = 1260

Приклад 2: Якими будуть складні відсотки на 8000 рупій через два роки, якщо відсоткова ставка становить 2% річних?

рішення:

враховуючи,

• Основний P = 8000
• Ставка r = 2%
• Термін = 2 роки

за формулою

A = P (1 + R/100) ^п

A = 8000 (1 + 2/100)²= 8000 (102/100)²

А = 8323

Складні відсотки = A – P = 8323 – 8000 = 323 рупії

Приклад 3: Харі вніс на депозит рупій. 4000 у фінансовій компанії на 2 роки під 5% річних. Який складний відсоток отримує Рохіт через 2 роки?

рішення:

враховуючи,

• Основний P = 4000
• Ставка r = 5%
• Час = 2 роки

За формулою,

A = P (1 + R/100)^п

A= 4000 (1 + 5/100)²

A= 4000 (105/100)²

A = 4410

Складні відсотки = A – P = 4410 – 4000 = 410

Приклад 4: Знайдіть складні відсотки на рупій. 2000 р. за ставкою 4 % річних на 1,5 роки. Коли відсотки нараховуються кожні півроку?

рішення:

враховуючи,

• Основний p = 2000
• Ставка r = 4%
• Час = 1,5 (тобто 3 півроку)

за формулою,

A = P (1 + R/200) ^2н

A = 2000 (1 + 4/200) ³

A = 2000 (204/200) ³

А = 2122

Складні відсотки = A – P = 2122 – 2000 = 122

Приклад 5: Який складний відсоток на 10000 за один рік за ставкою 20% річних, якщо відсотки нараховуються щокварталу?

рішення:

враховуючи,

• Основний P = 10000 рупій
• Ставка R = 12% (12/4 = 3% за квартал рік)
• Час = 1 рік (1 × 4 = 4 квартали)

За формулою,

A = P (1 + R/100) ^п

A = 10000 (1 + 3/100) ⁴

A = 10000 (103/100) ⁴

А = 11255

Складні відсотки = A – P = 11255 – 10000 = 1255

Приклад 6: Знайдіть складний відсоток за ставкою 5% річних протягом 2 років на основну суму, яка через 2 роки за ставкою 5% річних дасть руп. 400 як прості відсотки.

рішення:

враховуючи,

• Прості відсотки, ЯКЩО = 400
• Ставка R = 5%
• Час T = 2 роки

За формулою,

Прості відсотки = (P × T × R)/100

⇒ P = (SI × 100)/T × R

P = (400 × 100)/2 × 5 Ставка складних відсотків = 5%

P = 40000/10 = 4000 рупій

Термін = 2 роки

За формулою,

A = P (1 + R/100)

A = 4000 (1 + 5/100)

А = 4410

Складні відсотки = A – P = 4410 – 4000 = 410

Приклад 7: Знайдіть складні відсотки на 30 000 рупій за 7% відсотка щорічно протягом двох років.

рішення:

• Основний P = 30000 рупій
• Ставка R = 7%
• Термін = 2 роки

За формулою,

A = P (1 + R/100) ^п

A = 30000 (1 + 7/100) ²

A = 30000 (107/100) ²

А = 34347

Складні відсотки = A – P = 34347 – 30000 = 4347

Пов’язане читання:

• Щоденні складні відсотки
• Щомісячні складні відсотки
• Розв’язання складних відсотків класу 8
• Складні відсотки – запитання та відповіді щодо здібностей
• Простий інтерес

Складні відсотки – практичні запитання

Різноманітні практичні запитання щодо складних відсотків:

Q1. Знайдіть суму, яку потрібно сплатити через 3 роки, якщо суму 10 000 позичено за ставкою 4% щорічно.

Q2. Знайдіть відсотки, які необхідно сплатити через 1,5 роки, якщо суму 2500 позичено за ставкою 6% на півроку.

Q3. Розрахувати складні відсотки на позичену суму 9000 за ставкою 5% щокварталу протягом 15 місяців.

Q4. Розрахувати складні відсотки на суму 20000 позичених за ставкою 12% на 3 місяці, нараховуючи щомісяця

Висновок про складні відсотки

Складні відсотки - це a потужна фінансова концепція, яка дозволяє інвестиціям або позикам зростати або накопичуватися з часом. На відміну від прості відсотки, які обчислюють лише відсотки на початкову основну суму, складні відсотки враховує відсотки, отримані як на початкову основну суму, так і на будь-які накопичені відсотки за попередні періоди.

Складні відсотки – поширені запитання

Що означають складні відсотки?

Складні відсотки — це відсотки, нараховані на основну суму, а також на попередні відсотки, отримані протягом фіксованого періоду часу

Як розрахувати складні відсотки?

Для розрахунку складних відсотків спочатку розраховується остаточна сума, потім вона віднімається від основної суми, щоб отримати остаточний складний відсоток. Сума розраховується за формулою,

A = P(1 + R/100) ^t

сортування вставкою в java

CI = A – P

Чи складні відсотки кращі за прості відсотки для інвесторів?

Так, для інвесторів складні відсотки набагато кращі, ніж прості відсотки.

Що таке формула складних відсотків, якщо вони нараховуються щодня?

Припустімо, що дана основна сума дорівнює P, ставка дорівнює R, а часовий інтервал дорівнює T років, тоді формула складних відсотків, коли вони нараховуються щодня, є:

A = P(1 + R/365) ^{{365 × T}}

Яка різниця між CI та SI?

Основна різниця між CI та SI полягає в тому, що SI – це відсотки, що нараховуються на основну суму, тоді як CI – це відсотки, які нараховуються на основну суму, а також на відсотки, накопичені на основну суму