До розуміння B дерево і Дерево B+ відмінності, ми повинні знати дерево B і дерево B+ окремо.
Що таке дерево B?
B дерево є самобалансуючим деревом, і це m-way дерево, де m визначає порядок дерева. Btree є узагальненням Двійкове дерево пошуку у якому вузол може мати більше ніж один ключ і більше двох дочірніх елементів залежно від значення м . У дереві B дані вказуються у відсортованому порядку з нижчими значеннями в лівому піддереві та вищими значеннями в правому піддереві.
c програма для двовимірного масиву
Властивості дерева В
Нижче наведено властивості дерева B:
- У дереві B усі листові вузли повинні бути на одному рівні, тоді як у випадку бінарного дерева листові вузли можуть бути на різних рівнях.
Розберемо цю властивість на прикладі.
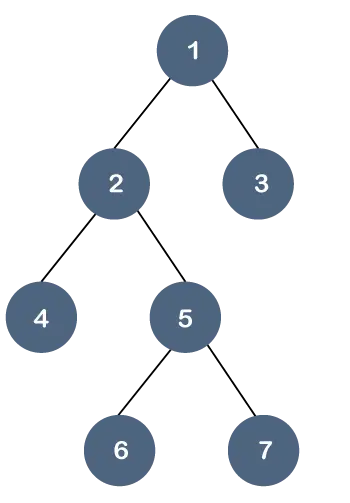
У наведеному вище дереві всі листкові вузли розташовані не на одному рівні, але вони мають найбільше двох дочірніх елементів. Тому можна сказати, що вищевказане дерево є a бінарне дерево але не дерево B.
- Якщо Btree має порядок m, то кожен вузол може мати максимум м У випадку мінімальних дочірніх вузлів листові вузли мають нуль дочірніх елементів, кореневий вузол має двох дочірніх вузлів, а внутрішні вузли мають стелю м/2.
- Кожен вузол може мати максимум (m-1) ключів. Наприклад, якщо значення m дорівнює 5, то максимальне значення ключів дорівнює 4.
- Кореневий вузол має мінімум один ключ, тоді як усі інші вузли, крім кореневого вузла, мають (стелю m/2 мінус - 1) мінімальні ключі.
- Якщо ми виконуємо вставку в дерево B, то вузол завжди вставляється в листовий вузол.
Припустімо, ми хочемо створити дерево B порядку 3, вставивши значення від 1 до 10.
Крок 1: Спочатку ми створюємо вузол із 1 значенням, як показано нижче:

крок 2: Наступний елемент — 2, який йде після 1, як показано нижче:

крок 3: Наступний елемент – 3, і він вставляється після 2, як показано нижче:

Оскільки ми знаємо, що кожен вузол може мати максимум 2 ключі, тому ми розділимо цей вузол через середній елемент. Середній елемент дорівнює 2, тому він переміщується до свого батька. Вузол 2 не має батьківського вузла, тому він стане кореневим вузлом, як показано нижче:

крок 4: Наступний елемент — 4. Оскільки 4 більше за 2 і 3, його буде додано після 3, як показано нижче:

крок 5: Наступний елемент — 5. Оскільки 5 більше за 2, 3 і 4, його буде додано після 4, як показано нижче:

Оскільки ми знаємо, що кожен вузол може мати максимум 2 ключі, тому ми розділимо цей вузол через середній елемент. Середній елемент дорівнює 4, тому він переміщується до свого батька. Батьківським є вузол 2; отже, 4 буде додано після 2, як показано нижче:

Крок 6: Наступний елемент — 6. Оскільки 6 більше за 2, 4 і 5, тому 6 буде після 5, як показано нижче:

Крок 7: Наступний елемент — 7. Оскільки 7 більше за 2, 4, 5 і 6, тому 7 буде після 6, як показано нижче:

Оскільки ми знаємо, що кожен вузол може мати максимум 2 ключі, тому ми розділимо цей вузол через середній елемент. Середній елемент має 6, тому він переміщується до свого батька, як показано нижче:

Але 6 не можна додати після 4, оскільки вузол може мати максимум 2 ключі, тому ми розділимо цей вузол через середній елемент. Середній елемент дорівнює 4, тому він переміщується до свого батька. Оскільки вузол 4 не має жодного батька, вузол 4 стане кореневим вузлом, як показано нижче:

Що таке дерево B+?
The Дерево B+ також відомий як просунуте самозбалансоване дерево, оскільки кожен шлях від кореня дерева до листя дерева має однакову довжину. Тут однакова довжина означає, що всі листові вузли розташовані на одному рівні. Не станеться так, що частина листкових вузлів буде на третьому рівні, а частина — на другому.
Індекс дерева B+ вважається багаторівневим індексом, але структура дерева B+ не схожа на послідовні файли багаторівневого індексу.
Чому використовується дерево B+?
Дерево B+ використовується для дуже ефективного зберігання записів, зберігаючи записи в індексованому вигляді за допомогою індексованої структури дерева B+. Завдяки багаторівневій індексації доступ до даних стає швидшим і простішим.
Деревоподібна структура B+
Структура вузлів дерева B+ містить покажчики та ключові значення, показані на малюнку нижче:

Як ми можемо помітити у наведеній вище структурі вузла дерева B+, він містить n-1 ключових значень (k1до кn-1) і n покажчиків (стор1до сторп).
Значення ключів пошуку, розміщені у вузлі, зберігаються в порядку сортування. Таким чином, якщо i
Обмеження на різні типи вузлів
Нехай 'b' буде порядком дерева B+.
Non-Leaf вузол
Нехай «m» представляє кількість дітей вузла, тоді зв’язок між порядком дерева та кількістю дітей можна представити як:

Нехай k представляє значення ключів пошуку. Відношення між порядком дерева та ключем пошуку можна представити як:
Оскільки ми знаємо, що кількість покажчиків дорівнює значенням ключа пошуку плюс 1, математично це можна записати так:
Кількість вказівників (або дітей) = кількість клавіш пошуку + 1
Таким чином, максимальна кількість покажчиків буде 'b', а мінімальна кількість покажчиків буде максимальною функцією b/2.
Листковий вузол
Ліцевий вузол — це вузол, який знаходиться на останньому рівні B+ дерева, і кожен листовий вузол використовує лише один вказівник для з’єднання один з одним, щоб забезпечити послідовний доступ на листовому рівні.
У листовому вузлі максимальна кількість дочірніх елементів:

Максимальна кількість ключів пошуку:

Кореневий вузол
Максимальна кількість дітей у випадку кореневого вузла: b
Мінімальна кількість дітей: 2
Особливі випадки в дереві B+
Випадок 1: Якщо кореневий вузол є єдиним вузлом у дереві. У цьому випадку кореневий вузол стає листовим вузлом.
У цьому випадку максимальна кількість дочірніх елементів дорівнює 1, тобто сам кореневий вузол, тоді як мінімальна кількість дочірніх елементів дорівнює b-1, що є таким же, як і для листкового вузла.
Представлення листового вузла в B+ дереві

На наведеному вище малюнку «.» представляє вказівник, тоді як 10, 20 і 30 є ключовими значеннями. Покажчик містить адресу, за якою зберігається значення ключа, як показано на малюнку вище.
Приклад дерева B+
Кет тимпф чистий капітал

На наведеному вище малюнку вузол містить три ключові значення, тобто 9, 16 і 25. Покажчик, який з’являється перед 9, містить ключові значення менше 9, представлені ki. Покажчик, який з’являється перед 16, містить ключові значення, що перевищують або дорівнюють 9, але менше 16, представлені kj. Покажчик, який з’являється перед 25, містить ключові значення, що перевищують або дорівнюють 16, але менше 25, представлені kп.
Відмінності між B деревом і B+ деревом

Нижче наведено відмінності між деревом B і деревом B+:
| B дерево | Дерево B+ |
|---|---|
| У дереві B усі ключі та записи зберігаються як у внутрішніх, так і в листових вузлах. | У дереві B+ ключі – це індекси, що зберігаються у внутрішніх вузлах, а записи зберігаються у листових вузлах. |
| У дереві B ключі не можуть зберігатися повторно, що означає відсутність дублювання ключів або записів. | У дереві B+ може бути надмірність у появі ключів. У цьому випадку записи зберігаються у кінцевих вузлах, тоді як ключі зберігаються у внутрішніх вузлах, тому надлишкові ключі можуть бути присутніми у внутрішніх вузлах. |
| У дереві B листові вузли не пов’язані один з одним. | У дереві B+ листові вузли пов’язані один з одним, щоб забезпечити послідовний доступ. |
| У Btree пошук не дуже ефективний, оскільки записи зберігаються або в листі, або у внутрішніх вузлах. | У дереві B+ пошук дуже ефективний або швидший, оскільки всі записи зберігаються в листових вузлах. |
| Видалення внутрішніх вузлів є дуже повільним і трудомістким процесом, оскільки нам також потрібно враховувати дочірній елемент видаленого ключа. | Видалення в дереві B+ відбувається дуже швидко, оскільки всі записи зберігаються в листових вузлах, тому нам не потрібно враховувати дочірній елемент вузла. |
| У Btree послідовний доступ неможливий. | У дереві B+ усі листові вузли з’єднані один з одним через покажчик, тому можливий послідовний доступ. |
| У Btree виконується більша кількість операцій поділу, завдяки чому висота збільшується порівняно з шириною, | Дерево B+ має більшу ширину порівняно з висотою. |
| У Btree кожен вузол має принаймні дві гілки, і кожен вузол містить деякі записи, тому нам не потрібно переходити до листкових вузлів, щоб отримати дані. | У дереві B+ внутрішні вузли містять лише покажчики, а листкові вузли містять записи. Усі листові вузли знаходяться на одному рівні, тому нам потрібно пройти до листових вузлів, щоб отримати дані. |
| Кореневий вузол містить принаймні від 2 до m дітей, де m — порядок дерева. | Кореневий вузол містить принаймні від 2 до m дітей, де m — порядок дерева. |
