Бінарне дерево є збалансованим, якщо висота дерева дорівнює O(Log n), де n – кількість вузлів. Наприклад, дерево AVL підтримує висоту O(Log n), переконавшись, що різниця між висотами лівого та правого піддерев становить не більше 1. Червоно-чорні дерева підтримують висоту O(Log n), переконавшись, що число чорних вузлів на кожному шляху від кореня до листа є однаковим і що немає суміжних червоних вузлів. Збалансовані двійкові дерева пошуку хороші з точки зору продуктивності, оскільки вони забезпечують O(log n) часу для пошуку, вставки та видалення.

Збалансоване бінарне дерево – це двійкове дерево, яке відповідає 3 умовам:

• Висота лівого і правого дерева для будь-якого вузла не відрізняється більше ніж на 1.
• Ліве піддерево цього вузла також збалансоване.
• Праве піддерево цього вузла також збалансоване.

Один вузол завжди збалансований. Його також називають бінарним деревом із збалансованою висотою.

просте число в java

приклад :

що таке uri

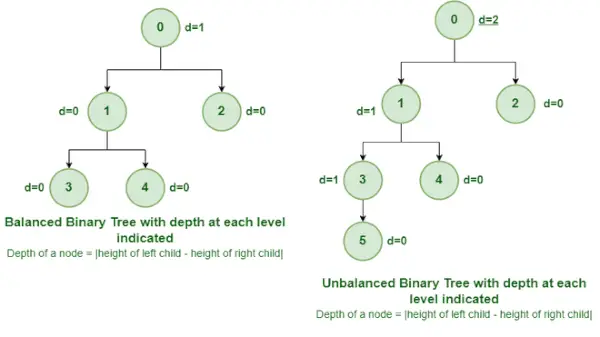
Збалансоване та незбалансоване бінарне дерево

Це тип бінарного дерева, в якому різниця між висотою лівого та правого піддерева для кожного вузла дорівнює 0 або 1. На малюнку вище кореневий вузол, що має значення 0, є незбалансованим із глибиною 2 одиниці. .

Застосування збалансованого бінарного дерева:

• Дерева AVL
• Червоне чорне дерево
• Збалансоване бінарне дерево пошуку

Переваги збалансованого бінарного дерева:

• Неруйнівні оновлення підтримуються збалансованим бінарним деревом з такою ж асимптотичною ефективністю.
• Діапазонні запити та ітерація в правильній послідовності стали можливими завдяки збалансованому бінарному дереву.