У геометрії кут є суттєвою мірою геометричної фігури. Кут визначається як ступінь повороту навколо точки перетину двох прямих або площин, які необхідні для приведення однієї у відповідність з іншою. Існують різні види кутів, засновані на вимірюванні кута. Вимірюється в градусах або радіанах. Кут — це фігура, утворена двома лініями або променями, які розходяться із спільної точки, яка називається вершиною. При перетині двох променів, тобто при проектуванні півпрямих із спільним кінцем, утворюється кут. Тепер загальні кінцеві точки називаються вершинами, а промені — рукавами.
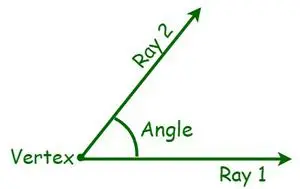
Види кутів

- Гострий кут: Гострий кут — це кут, який більше 0 градусів і менше 90 градусів, тобто коливається від 0° до 90° (обидва винятки).
- Прямий кут: Прямим кутом називають кут, який дорівнює рівно 90 градусам.
- Тупий кут: Тупим кутом називається кут, який перевищує 90 градусів і менше 180 градусів, тобто коливається від 90° до 180° (обидва винятки).
- Прямий кут: Прямим кутом називають кут, який дорівнює рівно 180 градусам.
- Кут рефлексу: Кут рефлексу – це кут, який перевищує 180 градусів і менше 360 градусів, тобто коливається від 180° до 360° (обидва виняткові).
- Повний кут або повний поворот: Повним кутом називають кут, який дорівнює рівно 360 градусам.
Існують також інші типи кутів, наприклад додаткові кути, додаткові кути, а також суміжні та несуміжні кути.
- Додаткові кути: Два кути називаються додатковими, якщо їх сума дорівнює прямому куту, тобто 90°.
- Додаткові кути: Два кути називаються додатковими, якщо їх сума дорівнює 180°.
- Суміжні кути: Два кути називаються суміжними, якщо вони мають спільну вершину і спільне плече.
- Несуміжні кути: Два кути називаються несуміжними, якщо вони не мають спільної вершини та спільного плеча.
Формула знаходження кутів
Існують різні види формул для знаходження кута; деякі з них — формула центрального кута, формула подвійного кута, формула півкута, формула складеного кута, формула внутрішнього кута тощо.
- Використовуємо формулу центрального кута, щоб визначити кут сегмента в колі.
- Ми використовуємо формулу суми внутрішніх кутів, щоб визначити відсутній кут у багатокутнику.
- Ми використовуємо тригонометричні співвідношення, щоб знайти відсутній кут прямокутного трикутника.
- Ми використовуємо закон синусів або закон косинусів, щоб знайти відсутній кут непрямокутного трикутника.
Назва формули | Формула | Як знайти невідомий кут? |
|---|---|---|
| Формула центрального кута | θ =(s × 360°)/2прТут s — довжина дуги, а r — радіус кола | Підставивши значення довжини дуги та радіуса кола, визначте кут відрізка, складеного в колі. |
| Формула суми внутрішніх кутів | 180°(n-2)Тут n — кількість сторін багатокутника | Щоб визначити невідомий внутрішній кут багатокутника, спочатку обчисліть суму всіх внутрішніх кутів за цією формулою, а потім відніміть суму всіх відомих кутів із результату. |
| Тригонометричні співвідношення | sin θ = протилежна сторона/гіпотенузаcos θ = прилегла сторона/гіпотенузаtan θ = протилежна сторона/прилегла сторона | Залежно від наявних двох сторін прямокутного трикутника виберіть одне з цих тригонометричних співвідношень, щоб знайти невідомий кут. рядок конвертера на дату |
| Закон синусів | a/sin A = b/sin B = c/sin CТут A, B і C — внутрішні кути трикутника, а a, b і c — їх відповідні протилежні сторони. | Коли ми знаємо дві сторони та невключений кут (або) два кути та невключену сторону, тоді закон синусів можна використовувати для визначення невідомих кутів трикутника. |
| Закон косинусів | a2= b2+ c2– 2bc cos Ab2= c2+ а2– 2ca cos Bв2= а2+ б2– 2ab cos CТут A, B і C — внутрішні кути трикутника, а a, b і c — їх відповідні протилежні сторони. | Коли нам відомі три сторони (або) дві сторони та включений кут, тоді закон косинусів можна використовувати для визначення невідомих кутів трикутника. |
Приклади запитань
Завдання 1. Знайти кут при вершині B даного трикутника за однією з тригонометричних формул для знаходження кутів.

рішення:
для кожного машинопису
враховуючи,
BC = 3 одиниці = прилегла сторона θ.
AC = 4 одиниці = протилежна сторона θ.
У цьому випадку ми знаємо як протилежну, так і суміжну сторони θ. Отже, ми можемо використовувати формулу дотичної, щоб знайти θ.
⇒ tan θ = протилежна сторона/прилегла сторона
⇒ tan θ = 4/3
⇒ θ = загар-1(4/3) ⇒ θ = 53,1°
Отже, кут при вершині В дорівнює 53,1°.
Запитання 2: Знайдіть кути при вершинах X і Y, якщо ∠Z = 35° і x = 3 дюйми, y = 8 дюймів і z = 3,5 дюйма.

рішення:
враховуючи,
∠Z = 35° і x = 6 дюймів, y = 3 дюйми і z = 3,5 дюймів
Оскільки ми знаємо всі три сторони та кут, ми можемо скористатися формулою правила синуса.
З формули правила синуса ми маємо
x/sin X = y/sin Y = z/sin Z
тепер,
y/sin Y = z/sin Z
⇒ 3/sin Y = 3,5/sin 35°
⇒ 3/без Y = 3,5/0,574 {Оскільки sin 35° = 0,574}
⇒ sin Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = sin−1(0,492) = 29,47°
Ми знаємо, що сума трьох кутів трикутника дорівнює 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
dateformat.format⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Отже, ∠X = 115,53° і ∠Y = 29,47°.
Запитання 3: Обчисліть п’ятий внутрішній кут п’ятикутника, якщо чотири з його внутрішніх кутів дорівнюють 110°, 85°, 136° і 105°.
рішення:
Кількість сторін п'ятикутника (n) = 5.
Тепер сума всіх 5 внутрішніх кутів п'ятикутника = 180 (n -2)°
= 180 (5 – 2)° = 540°.
Сума даних 4 внутрішніх кутів = 110°+ 85°+ 136°+ і 105°= 436°.
Отже, п’ятий внутрішній кут = 540° – 436° = 104°
Отже, п’ятий внутрішній кут п’ятикутника дорівнює 104°.
Запитання 4: Визначте значення у, а також міру кутів на даному малюнку.
мікролітичне ядро

рішення:
З наведеного малюнка видно, що (4y – 6)° і (3y + 5)° є додатковими кутами, тобто сума (4y – 6)° і (3y + 5)° дорівнює 90 °.
⇒ (4y – 6)° + (3y + 5)° = 90°
⇒ (7y – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Тепер (4y – 6)° = (4 × 13 – 6)° = (52 – 6)° = 46°
(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
Завдання 5. Знайти кут при вершині Q у даному трикутнику за допомогою однієї з формул для знаходження кутів.

рішення:
Дано p = QR = 6 см, q = PR = 9 см і r = PQ = 7 см.
Оскільки ми знаємо всі три сторони та кут, ми можемо використовувати формулу правила косинуса, щоб знайти вершину кута Q.
⇒ q2= стор2+ р2– 2pr cos Q
⇒ 92= 62+ 72– 2 (6)(7) cos Q
⇒ 81 = 36 + 49 – 84 cos Q
⇒ 81 = 85 – 84cos Q
⇒84 cos Q = 81 – 85
⇒ 84 cos Q = -4
рядок масиву в c⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Отже, кут при вершині Q, ∠Q = 92,72°.
Завдання 6: Обчисліть кут сегмента в колі, якщо довжина дуги дорівнює 12π, а радіус 9 см.
рішення:
враховуючи,
Довжина дуги = 12π
Радіус (r) = 9 см
Тепер формула кута:
⇒ θ = (s×360°)/2пр
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 ×360°/10
⇒ θ = 240°
Отже, кут дорівнює 240°.
