Об'єм трикутної піраміди знаходять за формулою V = 1/3A.H . Трикутна піраміда, також відома як тетраедр, — це тип піраміди з трикутною основою та трьома трикутними гранями, які стикаються в одній точці, яка називається вершиною.

У цій статті ми детально дізнаємося про визначення піраміди, визначення трикутної піраміди, формулу трикутної піраміди, приклади та інші.

Зміст

переваги електрики

• Що таке піраміда?
• Визначення трикутної піраміди
• Формула трикутної піраміди
• Площа поверхні трикутної піраміди
• Об'єм трикутної піраміди

Що таке піраміда?

А піраміда класифікується на різні типи залежно від форми основи, наприклад, трикутна піраміда, квадратна піраміда, п’ятикутна піраміда, шестикутна піраміда тощо. Вершина — це точка зустрічі бічних поверхонь або бічних граней піраміди. . Перпендикулярна відстань від вершини піраміди до центру її основи є висотою або висотою піраміди. Перпендикулярна відстань між вершиною та основою похилої висоти бічної поверхні піраміди.

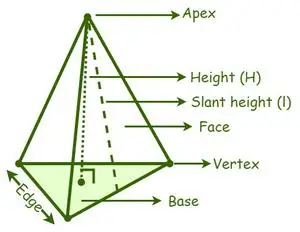
Піраміда

Визначення трикутної піраміди

Трикутна піраміда це піраміда, в основі якої лежить трикутник. Він також відомий як тетраедр і має три грані трикутної форми та одну трикутну основу, де трикутна основа може бути скалярною, рівнобедреною або рівностороннім трикутником. Трикутник далі класифікується на три типи, тобто правильна трикутна піраміда, неправильна трикутна піраміда та правильна трикутна піраміда.

• Правильна трикутна піраміда: Трикутна піраміда, чотири грані якої є рівносторонніми трикутниками, називається правильною трикутною пірамідою. Оскільки піраміда складається з рівносторонніх трикутників, то всі її внутрішні кути дорівнюють 60°.

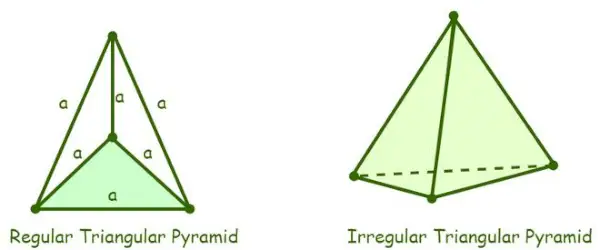
Визначення трикутної піраміди

• Неправильна трикутна піраміда: Неправильна трикутна піраміда - це така, у якої ребра основи не рівні, тобто основа неправильної трикутної піраміди є або трикутником у масштабі, або рівнобедреним трикутником. Усі трикутні піраміди вважаються правильними трикутними пірамідами, якщо тільки трикутна піраміда не вказана як неправильна.

• Правильна трикутна піраміда: Правильна трикутна піраміда — це піраміда, основою якої є прямокутний трикутник, а вершина розташована над центром основи.

Формула трикутної піраміди

Для трикутної піраміди є дві формули: площа поверхні трикутної піраміди та об’єм трикутної піраміди.

• Площа поверхні трикутної піраміди
  • Площа бічної поверхні трикутної піраміди
  • Загальна площа поверхні трикутної піраміди
• Об'єм трикутної піраміди

Площа поверхні трикутної піраміди

Площа поверхні піраміди має два типи площ поверхні, а саме: площа бічної поверхні та загальна площа поверхні, де площа поверхні піраміди є сумою площ бічних поверхонь, або бічних граней, і площі основи піраміди.

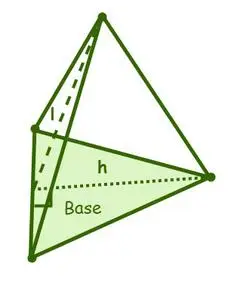
Площа поверхні трикутної піраміди

Площа бічної поверхні трикутної піраміди

Площа бічної поверхні трикутної піраміди обчислюється за формулою:

Площа бічної поверхні трикутної піраміди (LSA) = ½ × периметр × похила висота

Загальна площа поверхні трикутної піраміди

Загальна площа поверхні піраміди (TSA) = площа бічної поверхні піраміди + площа основи

Отже, TSA = ½ × периметр × похила висота + ½ × основа × висота

Загальна площа поверхні трикутної піраміди (TSA) = ½ × P × l + ½ bh

де,

• П це периметр основи
• л це похила висота піраміди
• b є основою трикутника в основі
• ч це висота піраміди

Об'єм трикутної піраміди

Об'єм піраміди - це загальний простір, укладений між усіма гранями піраміди. Об’єм піраміди зазвичай позначають літерою V, а її формула дорівнює одній третині добутку площі основи на висоту піраміди.

Формула об’єму піраміди задається так:

Об’єм трикутної піраміди = 1/3 × площа основи × висота

V = 1/3 × AH кубічних одиниць

де,

• IN є об'ємом піраміди
• А це площа основи піраміди
• Х це висота або висота піраміди

Формула об’єму правильної трикутної піраміди задається так

Об’єм правильної трикутної піраміди = a ³ /6√2 кубічних одиниць

Де a це довжина ребер

Стаття, що стосується трикутної піраміди:

• Прямокутна піраміда
• Квадратна піраміда
• П'ятикутна піраміда
• Шестикутна піраміда
• Об'єм формули піраміди
• Формула площі поверхні піраміди

Приклади на формулу трикутної піраміди

Приклад 1. Визначте об’єм трикутної піраміди з площею основи та висотою 50 см ² і 12 см відповідно.

рішення:

Дані дані,

• Площа основи трикутника = 100 см²
• Висота піраміди = 12 см

ми це знаємо,

Об’єм трикутної піраміди (V) = 1/3 × Площа трикутної основи × Висота

H = 1/3 × 50 × 12 = 200 см³

Отже, об’єм даної трикутної піраміди дорівнює 200 см³.

Приклад 2: Знайдіть загальну площу поверхні правильної трикутної піраміди, якщо довжина кожного ребра дорівнює 8 дюймів.

рішення:

Дані дані,

• Довжина кожного ребра правильної трикутної піраміди (а) = 8 дюймів

ми це знаємо,

Загальна площа поверхні правильної трикутної піраміди = √3a²

⇒ TSA = √3 × 8²

= 64√3 = 110,851 кв. дюйм

Отже, загальна площа поверхні правильної трикутної піраміди становить 110,851 кв.

Приклад 3: Визначте об’єм правильної трикутної піраміди, якщо довжина ребра дорівнює 10 см.

рішення:

Дані дані,

• Довжина кожного ребра правильної трикутної піраміди (а) = 10 см

ми це знаємо,

Об’єм правильної трикутної піраміди = а³/6√2

⇒ V = (10)³/6√2

= 1000/6√2 = 117,85 см³

Отже, об'єм правильної трикутної піраміди дорівнює 117,85 куб. см.

Приклад 4: Знайдіть похилу висоту трикутної піраміди, якщо площа її бічної поверхні дорівнює 600 квадратних дюймів, а периметр основи дорівнює 60 дюймів.

java випадкова математика випадкова

рішення:

Дані дані,

• Площа бічної поверхні = 600 кв
• Периметр основи = 60 дюймів

ми це знаємо,

Площа бічної поверхні = ½ × периметр × похила висота

600 = ½ × 60 × л

l = 600/30 = 20 дюймів

Отже, похила даної піраміди дорівнює 20 дюймів.

Приклад 5: Визначте повну площу поверхні трикутної піраміди, площа основи якої дорівнює 28 см2, периметр трикутника — 18 см, а похила висота піраміди — 20 см.

рішення:

Дані дані,

• Площа трикутної основи = 28 см²
• Висота нахилу (l) = 20 см
• Периметр (P) = 18 см

ми це знаємо,

Загальна площа поверхні (TSA) трикутної піраміди = ½ × периметр × похила висота + площа основи

⇒ TSA = ½ × 18 × 20 + 28

= 180 + 28 = 208 см кв

Отже, повна площа поверхні даної піраміди дорівнює 208 кв.см.

Практичні завдання на формулу трикутної піраміди

Q1. Дано трикутну піраміду з площею основи 15 квадратних одиниць і висотою 10 одиниць. Який об’єм піраміди?

Q2. Дано правильну трикутну піраміду з кожним ребром основи рівностороннього трикутника, що дорівнює 6 одиницям, яка загальна площа поверхні піраміди?

Q3. Дано правильну трикутну піраміду, кожне ребро рівносторонньої трикутної основи має розміри 4 одиниці та висоту 5 одиниць, які об’єм і загальна площа поверхні піраміди?

Q4. Якщо довжини сторін основи трикутної піраміди дорівнюють 3 одиницям, 4 одиницям і 5 одиницям, а висота піраміди дорівнює 12 одиницям, чому дорівнює об’єм піраміди?

Q5. Яка повна площа трикутної піраміди з основою у формі прямокутного трикутника з катетами 3 і 4 одиниці та гіпотенузою 5 одиниць, якщо висота піраміди від основи до вершини становить 10 одиниць ?

Поширені запитання щодо формули трикутної піраміди

Що таке визначення трикутної піраміди?

Трикутна піраміда - це геометрична фігура, яка має трикутну основу і три трикутні грані, що мають спільну вершину.

Скільки граней і вершин має трикутна піраміда?

Трикутна піраміда має чотири грані і чотири вершини. Одна вершина є спільною для всіх трьох граней піраміди.

Що таке основна формула для піраміди?

Основні формули піраміди:

• LSA = ½ × периметр × нахилена висота
• TSA = ½ × P × l + ½ bh
• V = 1/3 × AH

Які бувають види трикутних пірамід?

Існує три типи трикутних пірамід

• Правильна трикутна піраміда
• Неправильна трикутна піраміда
• Прямокутна трикутна піраміда

Що таке формула для трикутників?

Формула площі трикутника:

• (Площа)A = 1/2 × b × h