Можна виміряти три виміри: довжину, ширину та висоту будь-якого об’єкта, який ви можете побачити або торкнутися. Існують певні розміри нашого дому, в якому ми живемо. Прямокутний екран/монітор, на який ви дивитеся, має ширину та ширину своєї довжини. Для кожної тривимірної геометричної структури вимірюється площа поверхні та об’єм.
Повітря, покрите поверхнею об’єкта, — це площа поверхні будь-якого об’єкта. Тоді як кількість простору, доступного в об’єкті, є об’ємом.
Зміст
- Область поверхні
- Загальна площа поверхні
- Площа вигнутої поверхні/площа бічної поверхні
- Обсяг
- Приклади на площі поверхонь та об’єми
- Поширені запитання про формули площі поверхні та об’єму
Область поверхні
Площу поверхні та об’єм можна обчислити для будь-якої тривимірної (3D)геометричної форми. Поверхня будь-якої області - це область, зайнята поверхнею предмета. Об’єм – це кількість простору, доступного в об’єкті. У нас є різні типи форм, наприклад півсфера, сфера, куб, куб, циліндр тощо. Усі тривимірні форми мають площу та об’єм. Але двовимірні форми, такі як квадрати, прямокутники, трикутники, кола тощо.
Тут у двох вимірах ми можемо виміряти лише площу. Площа, яку займає тривимірний об'єкт своєю зовнішньою поверхнею, називається площею поверхні. Вимірюється в квадратних одиницях.
Область буває двох видів:
- Загальна площа поверхні
- Площа вигнутої поверхні/площа бічної поверхні
Загальна площа поверхні
Площа, включаючи основу (основи) і вигнуту частину, відповідає загальній площі поверхні. Це розмір площі, обмеженої поверхнею об’єкта. Якщо форма має вигнуту основу та поверхню, то сума двох областей буде загальною площею. Загальну площу поверхні можна визначити як загальну площу, покриту об’єктом, включаючи його основу, а також вигнуту частину. Якщо об'єкт має і базову, і вигнуту площі, тоді загальна площа поверхні дорівнюватиме сумі основи та вигнутої площі.
- Загальна площа поверхні — це загальна площа, яку займає об’єкт.
- Наприклад, візьмемо кубоїд як приклад, кубоїд має 6 граней, 12 ребер і 8 вершин.
Загальна площа поверхні = площа основи + вигнута площа
відкинути в sql
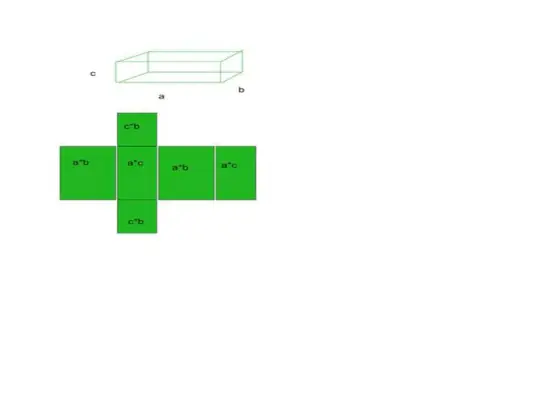
- Сума всіх цих 6 площ буде нашою загальною площею поверхні конкретної форми
приклад:
Нижче показано паралелепіпед, розміри якого дорівнюють довжині = 8 см, ширині = 4 см і висоті = 6 см. Знайдіть TSA кубоподібного паралелепіпеда.
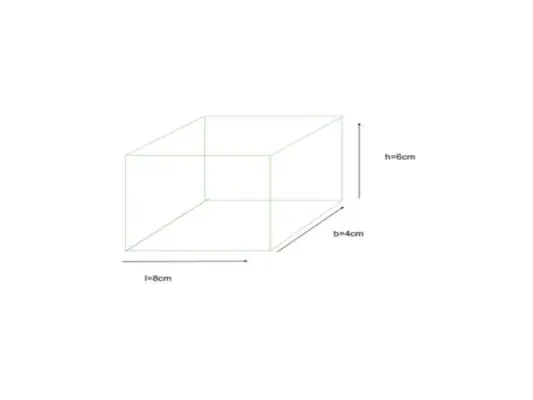
задано l = 8 см, b = 4 см, h = 6 см
TSA = 2((l * b) + (l * h) + (b * h))
= 2((8 * 4) + (8 * 6) + (4 * 6))
= 2((32) + (48) + (24))
= 2(104)
= 208
TSA кубоїда дорівнює 208 см.
Площа вигнутої поверхні/площа бічної поверхні
Площа вигнутої поверхні, за винятком її центру, відповідає площі лише вигнутої частини фігури (фігур). Для таких форм, як конус, її часто називають площею бічної поверхні. Площу бічної поверхні можна визначити як площу, яка включає лише вигнуту площу поверхні об’єкта або площу бічної поверхні об’єкта за винятком базової площі об’єкта. Площа бічної поверхні також відома як площа вигнутої поверхні.
Більшість фігур або об’єктів відносяться до площі вигнутої поверхні, форма або подібний до об’єкта циліндр відноситься до неї як до бічної поверхні. Простіше кажучи, область, яку ми видимі, називається площею бічної поверхні. Наприклад, розглянемо циліндр, як показано на малюнку нижче.
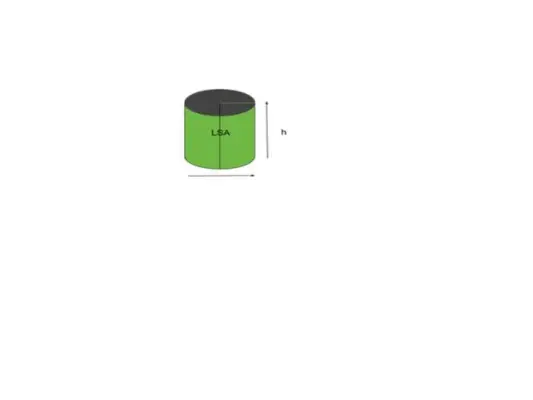
Обсяг
Об’єм – це кількість простору в певному 3D-об’єкті. Загальний обсяг простору, який займає предмет або речовина, називається об’ємом. Вимірюється в кубічних одиницях.
Формули площі поверхні та об’єму
Наведена таблиця містить загальну площу поверхні, площу вигнутої поверхні/площу бічної поверхні та об’єм різних форм.
| Назва форми | Площа вигнутої поверхні | Загальна площа поверхні | Обсяг |
|---|---|---|---|
| Кубоподібний | 2h(l + b) | 2 (lb + bh + hl) | l * b * h |
| куб | 4а2 | 6а2 | a3 |
| Циліндр | 2πrh | 2π(r + h) | πr2ч |
| Сфера | 4πр2 що таке вулик | 4πр2 | 4/3π р3 |
| Конус | πrl | πr(r + l) | 1/3π r2ч |
| Півкуля | 2пр2 | 3πр2 | 2/3π r3 |
Детальніше:
- Площа поверхні піраміди
- Площа поверхні циліндра
- Площа поверхні півкулі
- Площа поверхні сфери
- Площа поверхні кубоїда
Приклади на площі поверхонь та об’єми
Приклад 1: 2 кубики об’ємом 512 см кожен 3 з’єднуються впритул. Знайдіть площу поверхні отриманого кубоїда?
рішення:
враховуючи,
Об’єм (V) кожного куба = 512 см3
тепер ми можемо припустити, що a3= 512 см3
∴ Сторона куба, тобто a = 8 см
Тепер ширина і довжина отриманого прямокутного паралелепіпеда становитимуть 8 см кожна, а його висота становитиме 16 см.
Отже, площа поверхні кубоїда (TSA) = 2 (lb + bh + lh)
Тепер, склавши значення, ми отримаємо,
= 2(8 × 16 + 8 × 8 + 16 × 8) см 2
= (2 × 320) = 640 см 2
Отже, TSA кубоїда = 640 см 2
Приклад 2: У нас є циліндрична свічка діаметром 14 см і довжиною 2 см. Його розплавляють, утворюючи кубоподібну свічку розмірами 7 см × 11 см × 1 см. Скільки кубичних свічок можна отримати?
рішення:
Розміри циліндричної свічки:
Радіус циліндричної свічки = 14/2 см = 7 см
Висота/Товщина=2 см
Об'єм однієї циліндричної свічки = πr2h = π x 7 x 7 x (2) см3= 308 см3.
Об'єм кубоїда свічка = 7 х 11 х 1 = 77 см3
Отже, кількість кубоподібних свічок = об’єм кубоподібної свічки/об’єм однієї циліндричної свічки = 308/77 = 4
Отже, ми можемо отримати 4 свічки кубічної форми.
Приклад 3: Жінка хоче побудувати з глини сферичну іграшкову кулю, радіус якої дорівнює радіусу браслета, який вона носить. Враховуючи, що браслет має круглу форму, вона також хоче, щоб площа браслета дорівнювала об’єму кулі. Дізнайтеся радіус браслета, який вона носить?
рішення:
Нехай r — радіус браслета, а також сфери,
Нам дано, що об’єм кулі дорівнює площі браслета:
Отже,
πr2= 4/3 πр3
⇒ r = 3/4
Отже, радіус браслета дорівнює 3/4 одиниць.
Приклад 4: Дано, що похила прямого кругового конуса дорівнює 25 см, а його висота 24 см. Знайдіть площу кривої поверхні конуса?
рішення:
Формула площі вигнутої поверхні конуса дорівнює πrl. Де r — радіус конуса, а l — похила висота конуса.
Тут конус є правим круговим конусом.
Таким чином, радіус конуса буде:
r= sqrt{l^2 – h^2}
=>r = sqrt{25^2 – 24^2}
=> r = 7 см.
Тепер розрахунок кривої поверхні:
Необхідна площа = (22/7) * 7 * 25 = 550 см2
Отже, площа кривої поверхні конуса дорівнює 550 см 2 .
Приклад 5: Знайдіть площу бічної поверхні циліндра з радіусом основи 6 дюймів і висотою 14 дюймів.
підручник javafx
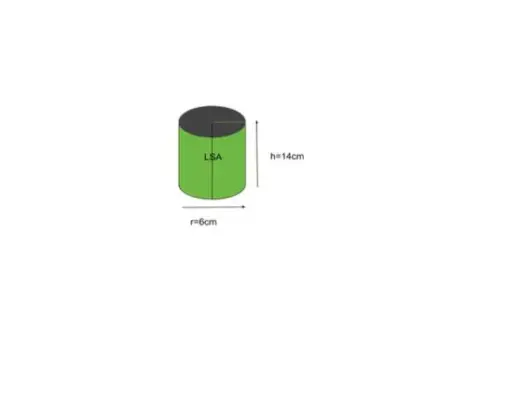
рішення:
Дано радіус r = 6, висота h = 14
LSA = 2∏п
= 2 * ∏ * 6 * 14
= 168∏
= 527 787
= 528.
LSA даного циліндра дорівнює 528 см .
Практичне запитання про площі поверхонь та об’єми
різноманітні Практичні запитання щодо площі поверхні та об’єму формули:
Q1. Знайдіть площу поверхні куба зі стороною 5 см.
Q2. Обчисліть об’єм кулі радіусом 3 метри.
Q3. Визначте повну площу поверхні циліндра з радіусом 4 см і висотою 8 см.
Q4. Знайдіть об’єм конуса з радіусом 6 дюймів і висотою 10 дюймів.
Q5. Обчисліть площу поверхні прямокутної призми довжиною 7 м, шириною 4 м і висотою 6 м.
Поширені запитання про формули площі поверхні та об’єму
Які формули для площі поверхні та об’єму?
У статті вище додано різні формули площі поверхні та об’єму.
Яка формула для об’єму площі поверхні, клас 10?
Формула для площі поверхні та об'єму класу 10 містить:
| Назва форми | Площа вигнутої поверхні | Загальна площа поверхні | Обсяг |
|---|---|---|---|
| Кубоподібний тип змінної Java | 2h(l + b) | 2 (lb + bh + hl) | l × b × h |
| куб | 4а2 | 6а2 | a3 |
| Циліндр | 2πrh | 2π(r + h) | πr2ч |
| Сфера | 4πр2 | 4πр2 | 4/3π р3 |
| Конус | πrl | πr(r + l) | 1/3π r2ч |
| Півкуля | 2пр2 | 3πр2 | 2/3π r3 |
Яка формула кубоїда за площею поверхні та об’ємом?
- Площа поверхні кубоїда = 2 (lb + bh + hl)
- Об'єм Cubiod = l × b × h
Що таке площа поверхні та об’єм?
Площа поверхні - це площа всіх поверхонь твердого тіла, а його об'єм - це простір, який займає тверде тіло.
