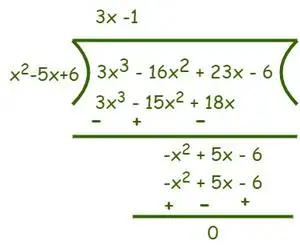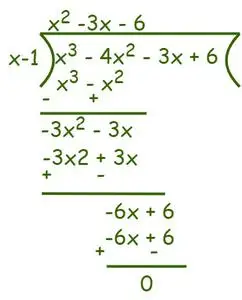Кубічне рівняння це математичне рівняння, в якому поліном третього ступеня прирівнюється до константи або іншого поліному максимального ступеня 2. Стандартним представленням кубічного рівняння є сокира ³ +bx ² +cx+d = 0 де a, b, c і d — дійсні числа. Деякі приклади кубічного рівняння x ³ – 4 рази ² + 15x – 9 = 0, 2x ³ – 4 рази ² = 0 тощо

Зміст

• Означення полінома
• Степінь рівняння
• Визначення кубічного рівняння
• Як розв'язувати кубічні рівняння?
• Розв’язування кубічних рівнянь
• Розв’язування кубічного рівняння за допомогою множників
• Розв’язування кубічного рівняння графічним методом
• Задачі на розв’язування кубічних рівнянь
• Тренувальні завдання на розв’язування кубічних рівнянь

Щоб навчитися розв’язувати кубічні рівняння, ми повинні спочатку дізнатися про поліноми, ступінь полінома та інші. У цій статті ми детально дізнаємось про багаточлени, поліноміальні рівняння, розв’язування кубічних рівнянь або як розв’язувати кубічні рівняння тощо.

Означення полінома

Поліном визначається наступним чином,

А поліном — алгебраїчний вираз, у якому ступінь змінної є цілим невід’ємним числом. Загальний вигляд многочлена — а₀x^п+ а₁x^n-1+ а₂x^n-2+… + а_п. Залежно від максимального ступеня змінної поліном можна класифікувати як моном, біном, тричлен тощо.

Що таке рівняння?

Рівняння визначається наступним чином:

Рівняння - це поліном, який прирівнюється до числового значення або будь-якого іншого многочлена. Наприклад, x + 2 — поліном, а x + 2 = 5 — рівняння. Аналогічно, 2x + 3 = x + 1 також є рівнянням, тоді як 2x + 3 і x + 1 є поліномами окремо.

Степінь рівняння

Визначення ступеня рівняння наведено нижче:

string.valueof java

Степінь рівняння визначається як максимальна потужність, якою володіє змінна в рівнянні.

Залежно від рівня рівняння, рівняння можна класифікувати таким чином:

• Лінійне рівняння
• Квадратне рівняння
• Кубічне рівняння
• Біквадратне рівняння

Лінійне рівняння

Рівняння, у якому максимальний ступінь змінної дорівнює 1, називається лінійним рівнянням.

• Наприклад, 3x +1 = 0

Квадратний поліном

Рівняння, у якому максимальний ступінь змінної дорівнює 2, є квадратним рівнянням.

• Наприклад 3x²+x+1 = 0

Кубічне рівняння

Рівняння, в якому максимальний ступінь змінної дорівнює 3, називається кубічним рівнянням.

• Наприклад 5x³+3x²+x+1 = 0

Біквадратичний поліном

Рівняння, у якому максимальний ступінь змінної дорівнює 4, називається біквадратичним поліномом або квадратним поліномом.

• Наприклад 5x⁴+4х³+3x²+2x+1 = 0

Визначення кубічного рівняння

Кубічне рівняння є алгебраїчним рівнянням, де найвищий ступінь полінома дорівнює 3. Деякі приклади кубічних рівнянь мають 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 тощо.

Загальний вигляд кубічного рівняння такий:

сокира ³ + bx ² + cx + d = 0, a ≠ 0

Де,

• а, б, і в – коефіцієнти змінної та їх експоненти і d є константою, а
• а, б, в і d є дійсними числами.

Як розв'язувати кубічні рівняння?

Кубічне рівняння — це рівняння третього ступеня. Він має три рішення, і його можна легко вирішити, виконавши кроки, додані нижче,

Крок 1: Знайдіть один розв’язок кубічного рівняння за допомогою методу «вдари та спробуй». Припустимо, що у нас є кубічне рівняння P(x), тоді знайдіть для будь-якого x = a, P(a) = 0, взявши x = 0, ±1, ±2, ±3, … і так далі.

Крок 2: Коли ми отримаємо P(a) = 0, знайдіть коефіцієнт (x – a) для P(x)

крок 3: Розділіть P(x) на (x – a), щоб отримати квадратне рівняння, скажімо Q(x), використовуючи поліноміальне ділення.

крок 4: Факторизуйте квадратне рівняння Q(x), щоб отримати множники (x – b) і (x – c).

крок 5: (x – a), (x – b) і (x – c) є множниками P(x), і розв’язуючи кожен множник, ми отримуємо корені рівняння as, a, b і c.

Дізнайтеся більше про, Ділення многочлена

Розв’язування кубічних рівнянь

А Кубічне рівняння можна вирішити двома способами

• Зводячи його до квадратного рівняння, а потім розв’язуючи його розкладанням на множники або квадратною формулою
• Графічним методом

А Кубічне рівняння має три корені. Ці корені можуть бути реальними або уявними. Крім того, можуть бути різні корені або два однакових і один різний корінь і всі три однакові корені.

Слід зазначити, що для будь-якого рівняння, в т.ч Кубічні рівняння , перш ніж розв’язувати рівняння, рівняння завжди потрібно оформляти в стандартній формі.

Наприклад, якщо дане рівняння дорівнює 2x²-5 = x + 4/x, тоді ми маємо переформатувати це у стандартну форму, тобто 2x³-x²-5x-4 = 0. Тепер ми можемо розв’язати рівняння будь-яким відповідним методом.

Розв’язування кубічного рівняння за допомогою множників

Розв’язання кубічного рівняння за допомогою факторної теореми пояснюється на прикладі, доданому нижче,

Приклад: Знайдіть корені рівняння f(x) = 3x ³ −16x ² + 23x − 6 = 0.

рішення:

Дано вираз: f(x) = 3x³−16x²+ 23x − 6 = 0

Спочатку розкладіть поліном на множники, щоб отримати корені

Оскільки константа дорівнює -6, можливі множники 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

карта проти набору

f(6) = 648 – 576 + 138 – 6 ≠ 0

Ми це знаємо, згідно з Факторна теорема якщо f(a) = 0, то (x-a) є фактором f(x)

Отже, (x – 2) і (x – 3) є множниками f(x). Отже, добуток (x – 2) і (x – 3) також буде множником f(x). Тепер, щоб знайти множники, що залишилися, скористайтеся методом довгого ділення та поділіть f(x) на добуток (x – 2) і (x – 3)

Отже, дільник = (x – 2)(x – 3) = (x²– 5x + 6) і Дивіденд = 3x³−16x²+ 23x − 6. Тепер розділіть, як показано нижче,

Після ділення ми отримуємо (3x-1) як приватне, а залишок дорівнює 0. Тепер згідно з Алгоритм ділення ми це знаємо Дивіденд = дільник × частка + залишок.

⇒ f(x) = (3x³−16x²+ 23x − 6) = (x²– 5x + 6)(3x-1)

Оскільки f(x) = 0

⇒ (x²– 5x + 6)(3x-1) = 0

⇒ x²– 5x + 6 = 0 або 3x-1 = 0

Тепер візьмемо 3x-1 = 0 ⇒ x = 1/3, оскільки ми вже знаємо два корені з x²– 5x + 6, що дорівнює 2 і 3

Так,

Коріння даного Кубічне рівняння дорівнюють 1/3, 2 і 3.

Розв’язування кубічного рівняння графічним методом

Кубічне рівняння розв’язується графічно, якщо ви не можете розв’язати дане рівняння за допомогою інших методів. Отже, нам потрібен точний малюнок даного кубічного рівняння. Корені рівняння – це точки(и), в яких графік перетинає вісь X, якщо рівняння складається з x, а якщо рівняння – з y, то корені рівняння – це точки, в яких графік розрізає вісь Y.

Кількість дійсних розв’язків кубічного рівняння дорівнює кількості разів, коли графік кубічного рівняння перетинає вісь X.

Приклад: знайдіть корені рівняння f(x) = x ³ − 4х ² − 9x + 36 = 0, використовуючи графічний спосіб.

рішення:

Дано вираз: f(x) = x³− 4х²− 9x + 36 = 0.

Тепер просто підставте випадкові значення для x на графік для заданої функції:

x	-4	-3	-2	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24	10	0	0	16

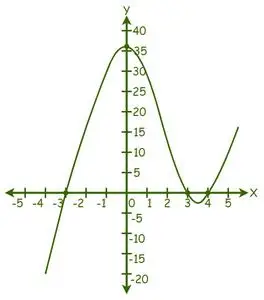
Ми бачимо, що графік перетинає вісь X у 3 точках, отже, існує 3 дійсних рішення.

З графіка розв’язки такі: x = -3, x = 3 і x = 4.

Отже, корені даного рівняння дорівнюють -3, 3 і 4.

Детальніше,

• Лінійне рівняння
• Розв’язування квадратного рівняння
• Розкладання поліномів на множники

Задачі на розв’язування кубічних рівнянь

Задача 1: Знайдіть корені f(x) = x ³ – 4 рази ² -3x + 6 = 0.

рішення:

Дано вираз: f(x) = x³– 4 рази²-3x + 6 = 0.

Спочатку розкладіть поліном на множники, щоб отримати корені.

c кодовий масив рядків

Оскільки константа дорівнює +6, можливі множники 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Отже, згідно з Факторна теорема (x – 1) є множником даного рівняння. Тепер, щоб знайти решту множників, використовуйте метод довгого ділення.

Відповідно до Алгоритм ділення ми можемо написати,

Отже, f(x) = x³– 4 рази²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 або (x²– 3x – 6) = 0

Ми знаємо, що корені квадратного рівняння ax²+ bx + c = 0 є,

x = [-b ± √(b²-4ac)]/2a

Отже, для (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Отже, корені даного кубічного рівняння дорівнюють 1, (3+√33)/2 і (3–√33)/2.

Задача 2: Знайдіть корені рівняння f(x) = 4x ³ – 10x ² + 4x = 0.

рішення:

Дано вираз: f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 або 4x – 2 = 0, x – 2 = 0

⇒ x = 0 або x = 1/2 або x = 2

Отже, корені даного рівняння дорівнюють 0, 1/2 і 2.

Задача 3: Знайдіть корені рівняння f(x) = x ³ + 3х ² + x + 3 = 0.

рішення:

Дано вираз: f(x) = x³+ 3х²+ x + 3 = 0.

⇒ x²(x + 3) + 1(x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 або x²+1 = 0

⇒ x = -3, ±i

Отже, задане рівняння має дійсний корінь, тобто -3, і два уявні корені, тобто ±i.

Задача 4: Знайдіть корені рівняння f(x) = x ³ – 7 разів ² – x + 7 = 0.

рішення:

Дані вирази,

f(x) = x³– 3 рази²– 5x + 7 = 0

Спочатку розкладіть рівняння на множники f(x): x³– 3 рази²– 5x + 7= 0

Його можна розкласти на (x-7)(x+1)(x-1) = 0

Розклавши поліном на множники, ми можемо знайти корені, прирівнявши кожен множник до нуля. Наприклад:

протоколи канального рівня

• x – 7 = 0, тому x = 7
• x + 1 = 0, тому x = -1
• x – 1 = 0, тому x = 1

Отже, корені рівняння f(x): x³– 3 рази²– 5x + 7 = 0 є

• х = 7
• х = -1
• х = 1

Задача 5: Знайдіть корені рівняння f(x) = x ³ − 6x ² + 11x − 6 = 0, використовуючи графічний метод.

рішення:

Дано вираз: f(x) = x³− 6x²+ 11x − 6 = 0.

Тепер просто підставте випадкові значення для x на графік для заданої функції:

x	1	2	3	4	5
f(x)	0	0	0	6	24

Ми бачимо, що графік перетинає вісь X у 3 точках, отже, існує 3 дійсних рішення.

З графіка розв’язки такі: x = 1, x = 2 і x = 3.

Отже, корені даного рівняння дорівнюють 1, 2 і 3.

Тренувальні завдання на розв’язування кубічних рівнянь

Нижче додано різні практичні задачі, пов’язані з кубічними рівняннями. Розв’яжіть ці задачі, щоб повністю зрозуміти концепцію Як розв’язати кубічне рівняння?

P1. Розв’яжіть кубічне рівняння, 3x³+ 2х²– 11x + 7 = 0.

P2. Знайдіть корені кубічного рівняння 4x³– 12 разів²+ 17 = 0.

P3. Розв’яжіть кубічне рівняння x³+ 4х²– x + 3 = 0 графічним методом.

P4. Знайдіть число, яке задовольняє -9x³+ 11x²– 8x + 2 = 0.

Поширені запитання щодо розв’язування кубічних рівнянь

1. Що таке кубічні рівняння?

Кубічні рівняння — це алгебраїчні рівняння, у яких максимальний ступінь змінної дорівнює 3

2. Як розкласти кубічне рівняння на множники?

Ми можемо розкласти кубічне рівняння двома способами. Спочатку взявши загальний лінійний вираз із заданого кубічного рівняння, тоді ми матимемо лінійний і квадратичний вираз як добуток. Це квадратне рівняння можна додатково розкласти на множники, щоб отримати всі множники. Другий спосіб полягає в тому, щоб знайти нуль даного кубічного рівняння шляхом приведення випадкових значень. Значення, для якого значення рівняння дорівнює нулю, буде одним із нулів даного кубічного рівняння. Тепер, використовуючи факторну теорему, сформуйте лінійний вираз, скажімо, x-a, і розділіть дане кубічне рівняння на цей вираз, який дасть квадратне рівняння як приватне. Отримане квадратне рівняння можна розкласти на множники, щоб отримати всі множники.

3. Як графічно розв’язати кубічне рівняння?

Щоб розв’язати кубічне рівняння, графічно помістіть випадкові значення x у задане кубічне рівняння та розв’яжіть, ви отримаєте значення y. Нанесіть отримані значення на графік. Знайдіть координати, в яких графік перетинає вісь х. Ці координати є рішенням кубічного рівняння.

4. Чи всі кубічні рівняння можна розв’язати точно?

Будь-яке рівняння непарного ступеня повинно мати один дійсний корінь. Отже, кубічне рівняння повинно мати принаймні один дійсний корінь, на відміну від квадратного рівняння, де обидва корені можуть бути уявними, коли дискримінант менше нуля.

5. Чи може кубічне рівняння мати декілька розв’язків?

Так, кубічні рівняння можуть мати кілька розв’язків, оскільки кубічне рівняння може мати до трьох різних дійсних коренів.

6. Що ви розумієте під ступенем рівняння?

Максимальна потужність, яку має змінна в рівнянні, називається ступенем полінома.

7. Яка різниця між многочленом і рівнянням?

Поліном — це просто алгебраїчне рівняння, у якому ступінь змінної є цілим невід’ємним числом. Коли цей поліном прирівнюється (=) до числового значення або іншого полінома, він називається рівнянням.

8. Що таке факторна теорема для кубічних рівнянь?

Факторна теорема стверджує, що якщо r є коренем (розв’язком) кубічного рівняння ax³+ bx²+ cx + d = 0, то x – r є множником рівняння.

cdr повна форма

9. Що робити, якщо я не можу знайти точні рішення за допомогою формул?

Якщо знайти точні рішення здається неможливим, ми можемо використати чисельні методи, такі як ітераційні методи (наприклад, метод Ньютона), щоб наблизити корені рівняння.

Дізнайтеся більше про Метод Ньютона Рафсона .