Реляційна алгебра є процедурною мовою запитів. Він надає крок за кроком процес отримання результату запиту. Він використовує оператори для виконання запитів.
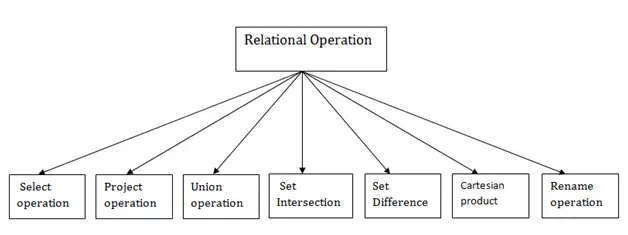
Типи реляційних операцій
1. Виберіть операцію:
- Операція select вибирає кортежі, які задовольняють заданий предикат.
- Позначається сигмою (σ).
Notation: σ p(r)
Де:
стор використовується для прогнозування вибору
r використовується для віднош
стор використовується як формула пропозиційної логіки, яка може використовувати такі сполучники, як: І АБО та НІ. Ці оператори відношення можна використовувати як оператори відношення, наприклад =, ≠, ≧, , ≦.
Наприклад: відносини ПОЗИКИ
| НАЗВА ГІЛКИ | LOAN_NO | СУМА |
|---|---|---|
| Центр міста | L-17 | 1000 |
| Секвоя | L-23 | 2000 рік |
| Перрірайд | L-15 | 1500 |
| Центр міста | L-14 | 1500 |
| Міанус | L-13 | 500 |
| Roundhill | L-11 | 900 |
| Перрірайд | L-16 | 1300 |
введення:
σ BRANCH_NAME='perryride' (LOAN)
Вихід:
python генерує uuid
| НАЗВА ГІЛКИ | LOAN_NO | СУМА |
|---|---|---|
| Перрірайд | L-15 | 1500 |
| Перрірайд | L-16 | 1300 |
2. Операція проекту:
- Ця операція показує список тих атрибутів, які ми хочемо відобразити в результаті. Решта атрибутів вилучаються з таблиці.
- Його позначають ∏.
Notation: ∏ A1, A2, An (r)
Де
A1 , A2 , A3 використовується як ім'я атрибута відношення r .
Приклад: ВІДНОСИНИ З КЛІЄНТАМИ
| ІМ'Я | ВУЛИЦЯ | МІСТО |
|---|---|---|
| Джонс | Головна | Гаррісон |
| Сміт | північ | Жито |
| Хейс | Головна | Гаррісон |
| Каррі | північ | Жито |
| Джонсон | Душа | Бруклін |
| Брукс | Сенатор | Бруклін |
введення:
∏ NAME, CITY (CUSTOMER)
Вихід:
алфавіт з цифрами
| ІМ'Я | МІСТО |
|---|---|
| Джонс | Гаррісон |
| Сміт | Жито |
| Хейс | Гаррісон |
| Каррі | Жито |
| Джонсон | Бруклін |
| Брукс | Бруклін |
3. Операція профспілки:
- Припустимо, є два кортежі R і S. Операція об’єднання містить усі кортежі, які знаходяться в R або S або обидва в R & S.
- Це усуває повторювані кортежі. Його позначають ∪.
Notation: R ∪ S
Операція об’єднання повинна відповідати такій умові:
- R і S повинні мати атрибут одного номера.
- Повторювані кортежі видаляються автоматично.
приклад:
ВІДНОСИНИ ВЛАДНИКА
| ІМ'Я КЛІЄНТА | НОМЕР РАХУНКУ |
|---|---|
| Джонсон | А-101 |
| Сміт | А-121 |
| Mayes | А-321 |
| Тернер | А-176 |
| Джонсон | А-273 |
| Джонс | А-472 |
| Ліндсей | А-284 |
ВІДНОСИНИ ПОЗИКИ
| ІМ'Я КЛІЄНТА | LOAN_NO |
|---|---|
| Джонс | L-17 |
| Сміт | L-23 |
| Хейс | L-15 |
| Джексон | L-14 |
| Каррі | L-93 |
| Сміт | L-11 |
| Вільямс | L-17 |
введення:
∏ CUSTOMER_NAME (BORROW) ∪ ∏ CUSTOMER_NAME (DEPOSITOR)
Вихід:
javatpoint java
| ІМ'Я КЛІЄНТА |
|---|
| Джонсон |
| Сміт |
| Хейс |
| Тернер |
| Джонс |
| Ліндсей |
| Джексон |
| Каррі |
| Вільямс |
| Mayes |
4. Встановити перетин:
- Припустимо, є два кортежі R і S. Операція перетину набору містить усі кортежі, які є в обох R і S.
- Його позначають перетином ∩.
Notation: R ∩ S
приклад: Використовуючи наведену вище таблицю DEPOSITOR і таблицю BORROW
введення:
∏ CUSTOMER_NAME (BORROW) ∩ ∏ CUSTOMER_NAME (DEPOSITOR)
Вихід:
| ІМ'Я КЛІЄНТА |
|---|
| Сміт |
| Джонс |
5. Встановити різницю:
- Припустимо, є два кортежі R і S. Операція перетину набору містить усі кортежі, які знаходяться в R, але не в S.
- Позначається перетином мінус (-).
Notation: R - S
приклад: Використовуючи наведену вище таблицю DEPOSITOR і таблицю BORROW
введення:
∏ CUSTOMER_NAME (BORROW) - ∏ CUSTOMER_NAME (DEPOSITOR)
Вихід:
| ІМ'Я КЛІЄНТА |
|---|
| Джексон |
| Хейс |
| Вільямс |
| Каррі |
6. Декартів добуток
- Декартовий добуток використовується для поєднання кожного рядка в одній таблиці з кожним рядком в іншій таблиці. Він також відомий як перехресний добуток.
- Він позначається X.
Notation: E X D
приклад:
СПІВРОБІТНИК
| EMP_ID | EMP_NAME | EMP_DEPT |
|---|---|---|
| 1 | Сміт | А |
| 2 | Гаррі | C |
| 3 | Джон | Б |
ВІДДІЛ
q1 q2 q3 q4
| DEPT_NO | DEPT_NAME |
|---|---|
| А | Маркетинг |
| Б | Продажі |
| C | юридичний |
введення:
EMPLOYEE X DEPARTMENT
Вихід:
| EMP_ID | EMP_NAME | EMP_DEPT | DEPT_NO | DEPT_NAME |
|---|---|---|---|---|
| 1 | Сміт | А | А | Маркетинг |
| 1 | Сміт | А | Б | Продажі |
| 1 | Сміт | А | C | юридичний |
| 2 | Гаррі | C | А | Маркетинг |
| 2 | Гаррі | C | Б | Продажі |
| 2 | Гаррі | C | C | юридичний |
| 3 | Джон | Б | А | Маркетинг |
| 3 | Джон | Б | Б | Продажі |
| 3 | Джон | Б | C | юридичний |
7. Операція перейменування:
Операція перейменування використовується для перейменування вихідного відношення. Він позначається ро (p).
приклад: Ми можемо використовувати оператор перейменування, щоб перейменувати відношення STUDENT на STUDENT1.
ρ(STUDENT1, STUDENT)
