Квантиль-квантиль (діаграма q-q) — це графічний метод для визначення, чи відповідає набір даних певному розподілу ймовірностей, чи дві вибірки даних походять з одного населення чи ні. Графіки Q-Q особливо корисні для оцінки того, чи є набір даних нормально розподілені або якщо він відповідає якомусь іншому відомому розподілу. Вони зазвичай використовуються в статистиці, аналізі даних і контролі якості для перевірки припущень і виявлення відхилень від очікуваних розподілів.
Квантилі та процентилі
Квантилі — це точки в наборі даних, які ділять дані на інтервали, що містять рівні ймовірності або частки загального розподілу. Вони часто використовуються для опису поширення або поширення набору даних. Найпоширеніші квантилі:
- Медіана (50 процентиль) : Медіана – це середнє значення набору даних, упорядковане від найменшого до найбільшого. Він ділить набір даних на дві рівні половини.
- Квартилі (25-й, 50-й і 75-й процентилі) : Квартилі ділять набір даних на чотири рівні частини. Перший квартиль (Q1) – це значення, нижче якого опускається 25% даних, другий квартиль (Q2) – це медіана, а третій квартиль (Q3) – це значення, нижче якого опускається 75% даних.
- Процентилі : Процентилі подібні до квартилів, але ділять набір даних на 100 рівних частин. Наприклад, 90-й процентиль – це значення, нижче якого опускається 90% даних.
Примітка:
- Графік q-q — це графік квантилів першого набору даних проти квантилів другого набору даних.
- Для довідкових цілей також нанесено лінію 45%; для якщо вибірки з однієї сукупності, то точки розташовані вздовж цієї лінії.
Нормальний розподіл:
Нормальний розподіл (він же розподіл Гаусса, крива Белла) — це неперервний розподіл ймовірностей, що представляє розподіл, отриманий із випадково згенерованих дійсних значень.
. 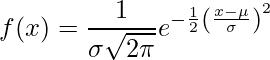

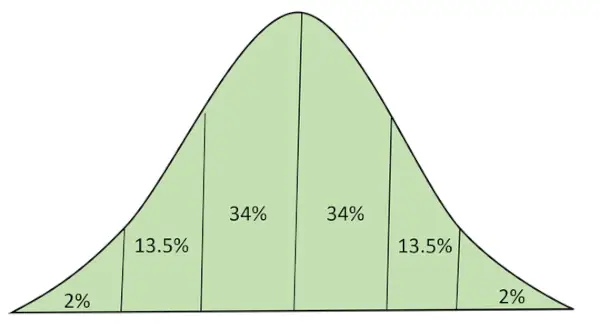
Нормальний розподіл із площею під кривою
Як намалювати діаграму Q-Q?
Щоб намалювати графік квантиль-квантиль (Q-Q), виконайте такі дії:
- Зберіть дані : Зберіть набір даних, для якого ви хочете створити графік Q-Q. Переконайтеся, що дані є чисельними та являють собою випадкову вибірку з досліджуваної сукупності.
- Сортування даних : упорядкуйте дані в порядку зростання або спадання. Цей крок важливий для точного обчислення квантилів.
- Виберіть теоретичний розподіл : визначте теоретичний розподіл, з яким ви хочете порівняти свій набір даних. Загальні варіанти включають нормальний розподіл, експоненціальний розподіл або будь-який інший розподіл, який добре відповідає вашим даним.
- Обчисліть теоретичні квантилі : обчисліть квантилі для вибраного теоретичного розподілу. Наприклад, якщо ви порівнюєте з нормальним розподілом, вам слід використати функцію оберненого інтегрального розподілу (CDF) нормального розподілу, щоб знайти очікувані квантилі.
- Складання сюжетів :
- Нанесіть відсортовані значення набору даних на вісь X.
- Нанесіть відповідні теоретичні квантилі на вісь ординат.
- Кожна точка даних (x, y) представляє пару спостережуваних і очікуваних значень.
- З’єднайте точки даних, щоб візуально перевірити зв’язок між набором даних і теоретичним розподілом.
Інтерпретація графіка Q-Q
- Якщо точки на графіку розташовані приблизно вздовж прямої лінії, це означає, що ваш набір даних відповідає передбачуваному розподілу.
- Відхилення від прямої вказують на відхилення від передбачуваного розподілу, що вимагає подальшого дослідження.
Вивчення подібності розподілу за допомогою графіків Q-Q
Дослідження подібності розподілу за допомогою графіків Q-Q є фундаментальним завданням статистики. Порівняння двох наборів даних, щоб визначити, чи походять вони з одного розподілу, є життєво важливим для різних аналітичних цілей. Коли виконується припущення про загальний розподіл, об’єднання наборів даних може підвищити точність оцінки параметрів, наприклад для розташування та масштабу. Графіки Q-Q, скорочення від квантильно-квантильних графіків, пропонують візуальний метод оцінки подібності розподілу. На цих графіках квантилі з одного набору даних порівнюються з квантилями з іншого. Якщо точки щільно вирівнюються вздовж діагональної лінії, це свідчить про подібність між розподілами. Відхилення від цієї діагональної лінії вказують на відмінності в характеристиках розподілу.
Хоча тести, як хі-квадрат і Колмогорова-Смирнова тести можуть оцінити загальні відмінності розподілу, діаграми Q-Q забезпечують детальну перспективу шляхом прямого порівняння квантилів. Це дає змогу аналітикам розпізнати конкретні відмінності, такі як зміни в місці розташування або зміни в масштабі, які можуть бути неочевидними лише за допомогою формальних статистичних тестів.
Реалізація графіка Q-Q на Python
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Вихід:
Графік Q-Q
Тут, оскільки точки даних приблизно йдуть прямою лінією на графіку Q-Q, це означає, що набір даних узгоджується з припущеним теоретичним розподілом, який у цьому випадку ми припустили як нормальний розподіл.
Переваги діаграми Q-Q
- Гнучке порівняння : графіки Q-Q можуть порівнювати набори даних різних розмірів без вимагають однакових розмірів вибірки.
- Безрозмірний аналіз : вони безрозмірні, що робить їх придатними для порівняння наборів даних різні одиниці або шкали.
- Візуальна інтерпретація : забезпечує чітке візуальне представлення розподілу даних порівняно з теоретичним розподілом.
- Чутливий до відхилень : легко виявляє відхилення від передбачуваних розподілів, допомагаючи у виявленні розбіжностей у даних.
- Діагностичний інструмент : допомагає в оцінці припущень щодо розподілу, виявленні викидів і розумінні моделей даних.
Застосування квантильно-квантильної графіки
Діаграма «Квантиль-Квантиль» використовується для таких цілей:
- Оцінка припущень щодо розподілу : графіки Q-Q часто використовуються для візуальної перевірки того, чи відповідає набір даних певному розподілу ймовірностей, наприклад нормальному розподілу. Порівнюючи квантилі даних спостереження з квантилями припущеного розподілу, можна виявити відхилення від припущеного розподілу. Це має вирішальне значення в багатьох статистичних аналізах, де достовірність припущень щодо розподілу впливає на точність статистичних висновків.
- Виявлення викидів : Викиди – це точки даних, які значно відрізняються від решти набору даних. Графіки Q-Q можуть допомогти визначити викиди, виявляючи точки даних, які далекі від очікуваної моделі розподілу. Викиди можуть відображатися як точки, які відхиляються від очікуваної прямої лінії на графіку.
- Порівняння розподілів : графіки Q-Q можна використовувати для порівняння двох наборів даних, щоб побачити, чи походять вони з одного розподілу. Це досягається шляхом побудови графіка квантилів одного набору даних проти квантилів іншого набору даних. Якщо точки розташовані приблизно вздовж прямої лінії, це означає, що два набори даних взято з одного розподілу.
- Оцінка нормальності : графіки Q-Q особливо корисні для оцінки нормальності набору даних. Якщо точки даних на графіку точно йдуть по прямій лінії, це означає, що набір даних розподілено приблизно нормально. Відхилення від лінії свідчать про відхилення від нормального, що може вимагати подальшого дослідження або непараметричних статистичних методів.
- Перевірка моделі : у таких галузях, як економетрика та машинне навчання, графіки Q-Q використовуються для перевірки прогнозних моделей. Порівнюючи квантилі спостережуваних відповідей з квантилями, передбаченими моделлю, можна оцінити, наскільки добре модель відповідає даним. Відхилення від очікуваної моделі можуть вказувати на області, де модель потребує вдосконалення.
- Контроль якості : Графіки Q-Q використовуються в процесах контролю якості для моніторингу розподілу виміряних або спостережуваних значень у часі або між різними партіями. Відхилення від очікуваних моделей у сюжеті можуть сигналізувати про зміни в основних процесах, спонукаючи до подальшого дослідження.
Типи графіків Q-Q
Існує кілька типів графіків Q-Q, які зазвичай використовуються в статистиці та аналізі даних, кожен з яких підходить для різних сценаріїв або цілей:
- Нормальний розподіл : симетричний розподіл, де графік Q-Q показуватиме точки приблизно вздовж діагональної лінії, якщо дані дотримуються нормального розподілу.
- Правосторонній розподіл : розподіл, де графік Q-Q відображатиме шаблон, де спостережувані квантилі відхиляються від прямої лінії до верхнього кінця, що вказує на довший хвіст з правого боку.
- Лівосторонній розподіл : розподіл, де графік Q-Q демонструватиме шаблон, де спостережувані квантилі відхиляються від прямої лінії до нижнього кінця, що вказує на довший хвіст з лівого боку.
- Недостатній розподіл : розподіл, де графік Q-Q показує спостережувані квантилі, згруповані щільніше навколо діагональної лінії порівняно з теоретичними квантилями, що свідчить про меншу дисперсію.
- Надрозпорошений розподіл : Розподіл, де графік Q-Q відображатиме спостережувані квантилі, більш розширені або відхиляючись від діагональної лінії, що вказує на вищу дисперсію або дисперсію порівняно з теоретичним розподілом.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Вихід:
Графік Q-Q для різних розподілів
преіті зінта
