Момент інерції — властивість тіла при обертальному русі. Момент інерції — властивість обертових тіл, яка прагне протидіяти зміні обертального руху тіла. Вона подібна до інерції будь-якого тіла при поступальному русі. Математично момент інерції визначається як сума добутку маси кожної частинки на квадрат відстані від осі обертання. Вимірюється в одиницях кгм 2 .
Давайте докладніше дізнаємося про момент інерції в статті нижче.
Зміст
- Момент інерції Визначення
- Формула моменту інерції
- Фактори, що впливають на момент інерції
- Як розрахувати момент інерції?
- Формула моменту інерції для різних фігур
- Радіус обертання
- Теореми про момент інерції
- Моменти інерції для різних об'єктів
Момент інерції Визначення
Момент інерції - це схильність тіла до обертального руху, яка протидіє зміні його обертальний рух через зовнішні сили. Момент інерції поводиться як кутова маса і називається обертальною інерцією. Момент інерції аналогічний механічному Інертність тіла.
MOI визначається як величина, виражена сумою добутку маса кожної частинки з квадратом її відстані від осі обертання для будь-якої частинки, що здійснює обертальний рух.
Одиниця моменту інерції
Момент інерції — це скалярна величина, а одиницею моменту інерції в СІ є кгм 2 .
Розмірна формула моменту інерції
Оскільки момент інерції подається як добуток маси на квадрат відстані. Його розмірна формула визначається добутком розмірної формули маси на квадрат розмірної формули довжини. Розмірна формула моменту інерції: ML 2
Що таке інерція?
Інертність — властивість матерії, завдяки якій вона прагне чинити опір зміні стану свого руху. Це означає, що тіло в стані спокою намагається залишатися в стані спокою і протистояти будь-якій силі, яка намагається привести його в рух, а тіло в русі намагається продовжувати рух і протистояти будь-якій силі, яка намагається змусити його змінити величину його руху. З точки зору кількості, це дорівнює максимальній силі, яка намагається змінити свій стан руху .
Дізнайтеся більше про Інертність .
Формула моменту інерції
Момент інерції - це a скалярна величина . Математично добуток квадрата маси частинки на відстань до осі обертання називається моментом інерції частинки відносно осі обертання.
Загальна формула для визначення моменту інерції будь-якого об’єкта така:
Я = пан 2
де,
м є маса об'єкта'
r – відстань від осі обертання
Для тіла, що складається з безперервних нескінченно малих частинок, для обчислення моменту інерції використовується інтегральна форма моменту інерції.
I = ∫dI
Я =
int_{0}^{M} r^2 dm
Момент інерції системи частинок
Момент інерції системи частинок визначається формулою
I = ∑m i r i 2
де,
r i є перпендикулярною відстанню iтисчастинка від осі
м i є масою iтисчастинка
Наведене вище рівняння моменту інерції говорить про те, що момент інерції для системи частинок дорівнює сумі добутку маси кожної з них на квадрат відстані від осі обертання кожної частинки.
Для малюнка, наведеного нижче,
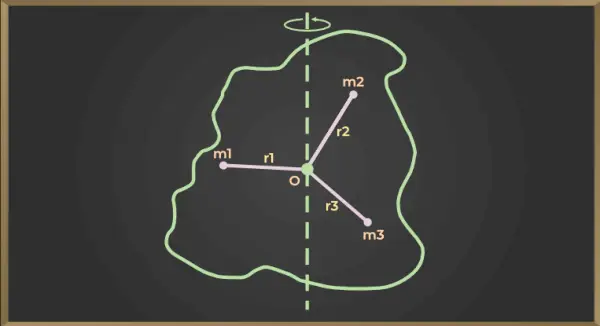
Момент інерції першої частинки = m1×r12
Момент інерції другої частинки = m2×r22
Момент інерції третьої частинки = m3×r32
Так само
Момент інерції nтисчастка = mп×rп2
Тепер момент інерції всього тіла відносно осі обертання АВ дорівнюватиме сумі моментів інерції всіх частинок, отже
I = m1×r12+ м2×r22+ м3×r32+……+мп×rп2
cout
I = Σm i ×r i 2
де,
я являють собою момент інерції тіла відносно осі обертання
м i є масою iтисчастинка,
r i є радіусом iтисчастинка
С являє собою суму.
З рівняння можна сказати, що момент інерції тіла відносно нерухомої осі дорівнює сумі добутку маси кожної частинки цього тіла на квадрат її перпендикулярної відстані від нерухомої осі.
Фактори, що впливають на момент інерції
Момент інерції будь-якого об'єкта залежить від наступних величин:
- Форма і розмір предмета
- Щільність матеріалу предмета
- Вісь обертання
Як розрахувати момент інерції?
Використовується кілька способів розрахувати момент інерції будь-якого об'єкта, що обертається.
- Для однорідних об’єктів момент інерції обчислюється шляхом добутку його маси на квадрат його відстані від осі обертання (r2).
- Для неоднорідних об’єктів ми обчислюємо момент інерції, беручи суму добутку мас окремих точок на кожному різному радіусі, для цього використовується формула:
I = ∑m i r i 2
Формула моменту інерції для різних фігур
У цій таблиці обговорюються вирази для моменту інерції для деяких симетричних об’єктів разом із віссю їх обертання:

| Об'єкт | Вісь | Вираз моменту інерції |
|---|---|---|
| Порожнистий циліндр тонкостінний | Центральний | Я = пан2 |
| Тонке кільце | Діаметр | I = 1/2 мр2 |
| Кільцеподібне кільце або порожнистий циліндр | Центральний | I = 1/2 M(r22+ р12) |
| Суцільний циліндр | Центральний | I = 1/2 мр2 |
| Однорідний диск | Діаметр | I = 1/4 мр2 |
| Порожниста сфера | Центральний | I = 2/3 мр2 |
| Тверда сфера | Центральний | I = 2/5 Mr2 |
| Однорідна симетрична сферична оболонка | Центральний | |
| Однорідна пластина або прямокутний паралелепіпед | Центральний | I = 1/12 M(a2+ б2) |
| Тонкий стрижень | Центральний | I = 1/12 Mr2 |
| Тонкий стрижень | Наприкінці Роду | I = 1/3 мр2 |
Радіус обертання
The Радіус обертання тіла визначається як перпендикулярна відстань від осі обертання до точки маси, маса якої дорівнює масі всього тіла, а момент інерції дорівнює фактичному моменту інерції об’єкта, як це було визначено. припустив, що там зосереджена вся маса тіла. Це уявна відстань. Радіус обертання позначається K.
Якщо маса і радіус обертання тіла М і К відповідно, то момент інерції тіла дорівнює
I = MK 2 ……(1)
Таким чином, радіус обертання тіла перпендикулярний до осі обертання, квадрат якого, помножений на масу цього тіла, дає момент інерції цього тіла відносно цієї осі.
Знову за рівнянням (1), К2= I/M
K = √(I/m)
Таким чином, радіус обертання тіла навколо осі дорівнює квадратному кореню з відношення тіла навколо цієї осі.
Теореми про момент інерції
Існує два типи теорем, які є дуже важливими щодо моменту інерції:
- Теорема паралельної осі
- Теорема про перпендикулярну вісь
Теорема про перпендикулярну вісь
Теорема про перпендикулярну вісь стверджує, що сума моментів інерції тіла відносно двох взаємно перпендикулярних осей, розташованих у площині тіла, дорівнює моменту інерції тіла відносно третьої осі, яка перпендикулярна до двох осей і проходить через їх точку. перетину.

На наведеному вище малюнку OX і LTD це дві осі в площині тіла, перпендикулярні одна одній. Третя вісь OZ яка перпендикулярна до площини тіла і проходить через точку перетину в OX і LTD сокири. Якщо я х , я і , і я с – це моменти інерції тіла відносно осі OX , LTD , і OZ осей відповідно, то згідно цієї теореми
я х + Я і = Я с
Теорема паралельної осі
Відповідно до Теорема паралельної осі , момент інерції тіла відносно даної осі дорівнює сумі моменту інерції відносно осі, що проходить через центр мас цього тіла, і добутку квадрата маси тіла на перпендикулярну відстань між дві осі.

Нехай на наведеному вище малюнку ми повинні знайти момент інерції я О тіла, що проходить через точку О і відносно осі, перпендикулярної до площини, а момент інерції тіла, що проходить через центр мас C а відносно осі, паралельної даній осі я C , то згідно з цією теоремою
я О = Я C + Ml 2
де
М це маса всього тіла
л — перпендикулярна відстань між двома осями.
Моменти інерції для різних об'єктів
Нижче в цій статті розглядається момент інерції різних об’єктів
Момент інерції прямокутної пластини
Якщо маса пластини дорівнює М, довжина l і ширина b, то момент інерції проходить через центр ваги і навколо осі, перпендикулярної площині пластини.

I = M(l 2 + б 2 / 12)
Момент інерції диска
Якщо диск має масу M і радіус r, то момент інерції відносно геометричної осі диска дорівнює

I = 1/2(Mr 2 )
Момент інерції стрижня
Якщо маса стрижня дорівнює M, а довжина l, то момент інерції відносно осі, перпендикулярної до довжини стержня і проходить через його центр тяжіння

I = ML 2 /12
Момент інерції кола
Якщо маса кільця дорівнює М, а радіус кільця дорівнює r, то момент інерції відносно осі, що проходить перпендикулярно до центру кільця, дорівнює

Я = пан 2
Момент інерції кулі
Якщо суцільна сфера має масу M і радіус r, то момент інерції відносно її діаметра дорівнює

I = 2/5Mr 2
Момент інерції суцільного циліндра
Момент інерції суцільного циліндра радіуса «R» і маси M визначається як

I = 1/2MR 2
Момент інерції порожнистого циліндра
Порожнистий циліндр має два радіуси, а саме внутрішній радіус і зовнішній радіус. Момент інерції порожнистого циліндра масою M, зовнішнім радіусом R1, а внутрішній радіус R2дається як
код фібоначчі java

I = 1/2M(R 1 2 + Р 2 2 )
Момент інерції твердої кулі
Момент інерції твердої кулі маси «M» і радіуса «R» подається як

I = 2/5MR 2
Момент інерції порожнистої кулі
Момент інерції порожнистої сфери масою M і радіусом «R» задається як

I = 2/3MR 2
Момент інерції кільця
Момент інерції кільця наведено для двох випадків, коли вісь обертання проходить через центр і коли вісь обертання проходить через діаметр.
Момент інерції кільця відносно осі, що проходить через центр, визначається як
перетворити рядок на int

Я = MR 2
Момент інерції кільця відносно осі, що проходить через діаметр, визначається як

Я = пан 2 /2
Момент інерції квадрата
Момент інерції квадрата сторони «а» подано як

Я = а 4 /12
Момент інерції квадратної пластини зі стороною довжини «l» і масою M задається як
I = 1/6ML 2
Момент інерції трикутника
Момент інерції трикутника дається для 3 ситуацій: перша, коли вісь проходить через центр, друга, коли вісь проходить через основу, і третя, коли вісь перпендикулярна до основи. Давайте подивимося на формулу для них одну за одною. Для трикутника з основою «b» і висотою «h» формула моменту інерції задається так:

Коли вісь проходить через центроїд
I = bh 3 /36
Коли вісь проходить через основу
I = bh 3 /12
Коли вісь перпендикулярна до основи
I = (hb/36)(b 2 – б 1 b + b 1 2 )
Різниця між моментом інерції та інерцією
Різниця між інерцією та моментом інерції наведена в таблиці нижче:
| Так ні. | Інертність | Момент інерції |
|---|---|---|
| 1. | Його важливість полягає в прямолінійному русі. | Його значення полягає в обертальному русі. |
| 2. | Це властивість об’єкта, яка протидіє зміні стану об’єкта під час прямолінійного руху. | Момент інерції - це така властивість об'єкта, яка протидіє зміні стану об'єкта при обертальному русі. |
| 3. | Інертність об'єкта залежить тільки від його маси. | Момент інерції тіла залежить від його маси та розподілу маси відносно осі обертання. |
| 4. | Інерція об'єкта фіксована. | Момент інерції об’єкта змінюється відносно різних осей обертання. |
Кінетична енергія тіла обертання
Припустимо, що тіло масою «m» обертається зі швидкістю v на відстані «r» від осі обертання. Тоді його кутова швидкість визначається як ω = v/r, тоді v = rω. Тепер ми знаємо, що Кінетична енергія тіла дається
KE = 1/2mv 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2ох2
⇒ KE = 1/2Iω 2
Отже, кінетична енергія тіла, що обертається, дорівнює половині добутку моменту інерції на кутова швидкість тіла. Також називають кінетичну енергію тіла, що обертається Кінетична енергія обертання . Формула кінетичної енергії обертання подана як
KE = 1/2Iω 2
Момент інерції (I) не залежить від кутової швидкості тіла. Вона є функцією маси тіла, що обертається, і відстані тіла від осі обертання. Отже, ми помічаємо, що кутовий рух аналогічний прямолінійному, це означає, що значення моменту інерції полягає в тому, що він дає уявлення про те, як маси розподіляються на різних відстанях від осі обертання в тілі, що обертається.
Застосування моменту інерції
Момент інерції має різні застосування, деякі з яких обговорюються нижче:
- Завдяки більшому моменту інерції Земля обертається навколо своєї осі з однаковою кутовою швидкістю.
- Під дитячим ігровим двигуном розміщено маленьке рухоме колесо. Після тертя цього колеса землею і виходу з двигуна завдяки моменту інерції колеса двигун ще деякий час продовжує працювати.
- Кожен двигун складається з великого і важкого колеса, прикріпленого до його валу, більша частина його маси знаходиться по колу. Тому його момент інерції великий. Це колесо називається маховиком. Крутний момент, який приводить в рух вал двигуна, продовжує зростати. Тому обертання вала може бути нерівномірним, але через наявність рухомого колеса з більшою інерцією вал продовжує обертатися з майже рівномірною швидкістю.
- У колесі волової вози, рикші, скутера, велосипеда тощо більша частина маси зосереджена на його колі чи ободі. цей обруч або рутина кріпиться до осі колеса жорсткими спицями. При цьому його момент інерції збільшується. Тому, коли під час їзди на велосипеді ноги перестають рухатися, колесо ще деякий час продовжує обертатися.
Також перевірте
- Кінематика обертального руху
- Рух Твердого Тіла
- Котильний рух
Розв’язані приклади на моменти інерції
Приклад 1: Тіло масою 500 г обертається навколо осі. відстань центру мас тіла від осі обертання 1,2 м. Знайдіть момент інерції тіла відносно осі обертання.
рішення:
Враховуючи, що M = 500 г = 0,5 кг, r = 1,2 м.
Очевидно, що всю масу тіла можна вважати розміщеною в його центрі мас. Тоді момент інерції тіла відносно осі обертання.
Я = пан2
I = 0,5 × (1,2)2
I = 0,72 кг·м2
Приклад 2. Радіус обертання тіла масою 1,2 кг навколо осі, віддаленої на 12 см від центру мас, дорівнює 13 см. Обчисліть радіус обертання і момент інерції відносно осі, що проходить через центр мас.
рішення:
Враховуючи, що M = 1,0 кг, K = 13 см, l = 12 см, KСМ= ?, яСМ= ?
З теореми про паралельність осі I = IСМ+ Ml2
К2= КCM2+ л2
або КCM2= К2– л2
КCM2 = (13)2– (12)2= 25
КСМ= 5
Тепер момент інерції ІСМ= МКCM2
яСМ= 1,0 × (0,05)2= 2,5 × 10-3кг м2
Приклад 3: Тіло масою 0,1 кг обертається навколо осі. якщо відстань центру мас тіла від осі обертання дорівнює 0,5 м, то знайти момент інерції тіла.
різниця між левом і тигром
рішення:
Враховуючи, що M = 0,1 кг і r = 0,5 м
тому я = пан2
I = 0,1 × (0,5)2
I = 0,025 кг·м2
Приклад 4: Момент інерції кілець відносно осі, що проходить через його центр перпендикулярно до площини круглого кільця, дорівнює 200 г/см. 2 . Яким буде момент інерції відносно його діаметра?
рішення:
Момент інерції кругового кільця відносно осі, що проходить через інший центр перпендикулярно його площині
МІСТЕР2= 200 г/см2
Момент інерції приблизно до діаметра
= 1/2 MR2
= 1/2 × 200 = 100 г/см2
Поширені запитання про моменти інерції
Як розрахувати момент інерції?
Основна формула для знаходження моменту інерції будь-якого однорідного тіла:
Я = пан 2
де,
м є маса об'єкта'
r – відстань від осі обертання
Як обчислити момент інерції балки?
Момент інерції балки вздовж центру та горизонтальної осі розраховується за формулою
I = ML 2 / 12
Від чого залежить момент інерції тіла?
Момент інерції будь-якого об'єкта залежить від наведених нижче факторів:
- Маса тіла,
- Вісь обертання
- Форма і розмір предмета
Що таке одиниця моменту інерції?
Одиницею моменту інерції є кгм 2
Чи може момент інерції бути негативним?
Ні, момент інерції ніколи не може бути негативним.
Що таке момент інерції маси?
Момент інерції маси — це вимірювання опору тіла зміні його кутового моменту або напрямку. Момент інерції маси для точкової маси визначається як I = mr2а для системи частинок момент інерції маси заданий як I = Σiмiri2
Що таке момент інерції площі?
Момент інерції площі — це властивість двовимірної фігурної площини, яка показує, як точки розосереджені відносно довільної осі на площині. Момент інерції площі також відомий як другий момент площі або квадратичний момент площі. Формула для площі моменту інерції в площині xy подана як Ixy= ∫xy dxdxy = ∫xy dA
