У реальному світі машинне навчання додатки зазвичай мають багато відповідних функцій, але лише частина з них може бути спостережуваною. Маючи справу зі змінними, які іноді спостерігаються, а іноді ні, справді можна використовувати випадки, коли ця змінна є видимою або спостерігається, щоб вивчати та робити прогнози для випадків, коли вона не спостерігається. Цей підхід часто називають обробкою відсутніх даних. Використовуючи доступні випадки, коли змінну можна спостерігати, алгоритми машинного навчання можуть вивчати закономірності та зв’язки зі спостережуваних даних. Потім ці вивчені шаблони можна використовувати для прогнозування значень змінної у випадках, коли вона відсутня або не спостерігається.
Алгоритм очікування-максимізації можна використовувати для обробки ситуацій, коли змінні частково спостерігаються. Коли певні змінні можна спостерігати, ми можемо використовувати ці випадки, щоб дізнатися та оцінити їх значення. Тоді ми можемо передбачити значення цих змінних у випадках, коли їх не можна спостерігати.
EM-алгоритм був запропонований і названий у основоположній статті, опублікованій у 1977 році Артуром Демпстером, Нан Лейрдом і Дональдом Рубіном. Їхня робота формалізувала алгоритм і продемонструвала його корисність у статистичному моделюванні та оцінці.
Алгоритм EM застосовний до латентних змінних, тобто змінних, які не спостерігаються безпосередньо, але виводяться зі значень інших спостережуваних змінних. Використовуючи відому загальну форму розподілу ймовірностей, що керує цими прихованими змінними, алгоритм EM може передбачити їхні значення.
Алгоритм EM служить основою для багатьох алгоритмів неконтрольованої кластеризації в області машинного навчання. Він забезпечує структуру для пошуку локальних параметрів максимальної правдоподібності статистичної моделі та виведення прихованих змінних у випадках, коли дані відсутні або неповні.
Алгоритм очікування-максимізації (EM).
Алгоритм очікування-максимізації (EM) — це ітеративний метод оптимізації, який поєднує різні неконтрольовані машинне навчання алгоритми для знаходження максимальної правдоподібності або максимальної апостеріорної оцінки параметрів у статистичних моделях, які включають неспостережувані приховані змінні. Алгоритм EM зазвичай використовується для моделей латентних змінних і може обробляти відсутні дані. Він складається з кроку оцінювання (E-крок) і кроку максимізації (M-крок), утворюючи ітераційний процес для покращення відповідності моделі.
- На кроці E алгоритм обчислює приховані змінні, тобто очікування логарифмічної ймовірності, використовуючи поточні оцінки параметрів.
- На кроці M алгоритм визначає параметри, які максимізують очікувану логарифм правдоподібності, отриману на кроці E, і відповідні параметри моделі оновлюються на основі оцінених прихованих змінних.

Очікування-максимізація в алгоритмі EM
Ітеративно повторюючи ці кроки, алгоритм EM прагне максимізувати ймовірність спостережуваних даних. Він зазвичай використовується для неконтрольованих завдань навчання, таких як кластеризація, де виводяться приховані змінні, і має застосування в різних сферах, включаючи машинне навчання, комп’ютерне зір і обробку природної мови.
Ключові терміни в алгоритмі очікування-максимізації (EM).
Деякі з найбільш часто використовуваних ключових термінів в алгоритмі очікування-максимізації (EM) такі:
- Приховані змінні: приховані змінні – це неспостережувані змінні в статистичних моделях, які можна зробити лише опосередковано через їхній вплив на спостережувані змінні. Їх неможливо безпосередньо виміряти, але можна виявити за їхнім впливом на спостережувані змінні. Вірогідність: це ймовірність спостереження даних за параметрами моделі. В алгоритмі EM мета полягає в тому, щоб знайти параметри, які максимізують імовірність. Логарифм правдоподібності: це логарифм функції правдоподібності, який вимірює відповідність між даними спостереження та моделлю. Алгоритм EM прагне максимізувати логарифм правдоподібності. Оцінка максимальної правдоподібності (MLE): MLE — це метод оцінки параметрів статистичної моделі шляхом знаходження значень параметрів, які максимізують функцію правдоподібності, яка вимірює, наскільки добре модель пояснює спостережувані дані. Апостеріорна ймовірність: у контексті байєсівського висновку алгоритм EM може бути розширений для оцінки максимальних апостериорних (MAP) оцінок, де апостеріорна ймовірність параметрів обчислюється на основі попереднього розподілу та функції ймовірності. Крок очікування (E): Е-крок алгоритму EM обчислює очікуване значення або апостеріорну ймовірність прихованих змінних, враховуючи спостережувані дані та поточні оцінки параметрів. Він передбачає обчислення ймовірностей кожної прихованої змінної для кожної точки даних. Крок максимізації (M): Крок M алгоритму EM оновлює оцінки параметрів шляхом максимізації очікуваної логарифмічної ймовірності, отриманої з E-кроку. Це передбачає пошук значень параметрів, які оптимізують функцію правдоподібності, зазвичай за допомогою числових методів оптимізації. Конвергенція: конвергенція відноситься до умови, коли алгоритм EM досягає стабільного рішення. Зазвичай це визначається шляхом перевірки того, чи зміна логарифмічної правдоподібності або оцінок параметрів опускається нижче попередньо визначеного порогу.
Як працює алгоритм очікування-максимізації (EM):
Суть алгоритму очікування-максимізації полягає у використанні доступних спостережених даних набору даних для оцінки відсутніх даних, а потім використання цих даних для оновлення значень параметрів. Давайте детально розберемося з алгоритмом ЕМ.

Блок-схема алгоритму ЕМ
- Ініціалізація:
- Спочатку розглядається набір початкових значень параметрів. Набір неповних спостережених даних надається системі з припущенням, що спостережувані дані походять від певної моделі.
- Обчисліть апостеріорну ймовірність або відповідальність кожної латентної змінної, враховуючи дані спостережень і поточні оцінки параметрів.
- Оцініть відсутні або неповні значення даних, використовуючи поточні оцінки параметрів.
- Обчисліть логарифм правдоподібності спостережуваних даних на основі поточних оцінок параметрів і оцінених відсутніх даних.
- Оновіть параметри моделі шляхом максимізації очікуваної повної правдоподібності журналу даних, отриманої на E-етапі.
- Зазвичай це включає розв’язання задач оптимізації, щоб знайти значення параметрів, які максимізують логарифм правдоподібності.
- Конкретний метод оптимізації, що використовується, залежить від характеру проблеми та моделі, що використовується.
- Перевірте збіжність, порівнюючи зміну логарифмічної правдоподібності або значень параметрів між ітераціями.
- Якщо зміна нижча за попередньо визначене порогове значення, зупиніться та вважайте, що алгоритм узгоджений.
- В іншому випадку поверніться до E-етапу та повторюйте процес, доки не буде досягнуто конвергенції.
Покрокова реалізація алгоритму очікування-максимізації
Імпортуйте необхідні бібліотеки
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
>
>
Створіть набір даних із двома компонентами Гауса
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
>
Вихід :

Графік щільності
Ініціалізація параметрів
Python3
jsp
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Виконайте ЕМ алгоритм
- Повторює задану кількість епох (у цьому випадку 20).
- У кожній епосі Е-крок обчислює відповідальність (значення гамми) шляхом оцінки щільності ймовірності Гауса для кожного компонента та зважування їх за відповідними пропорціями.
- М-крок оновлює параметри шляхом обчислення середнього зваженого значення та стандартного відхилення для кожного компонента
Python3
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
Вихід :

Епоха проти логарифмічної ймовірності
Нанесіть кінцеву оціночну щільність
Python3
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Вихід :
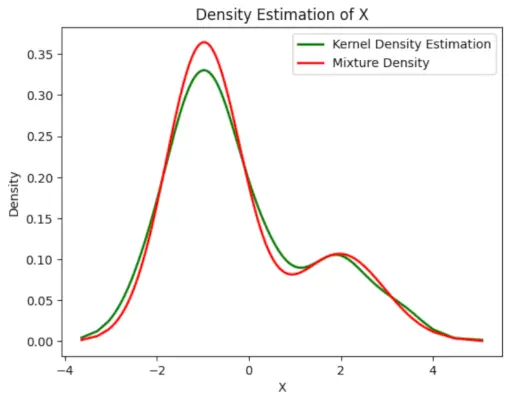
Розрахункова щільність
Застосування Алгоритм ЕМ
- Його можна використовувати для заповнення відсутніх даних у зразку.
- Його можна використовувати як основу неконтрольованого навчання кластерів.
- Його можна використовувати з метою оцінки параметрів прихованої марковської моделі (HMM).
- Його можна використовувати для виявлення значень прихованих змінних.
Переваги ЕМ-алгоритму
- Завжди гарантується, що ймовірність зростатиме з кожною ітерацією.
- Е-крок і М-крок часто досить прості для багатьох проблем з точки зору реалізації.
- Рішення М-кроків часто існують у закритому вигляді.
Недоліки ЕМ-алгоритму
- Має повільну конвергенцію.
- Він здійснює збіжність лише до локальних оптимумів.
- Вона вимагає обох ймовірностей, прямої та зворотної (числова оптимізація вимагає лише прямої ймовірності).
