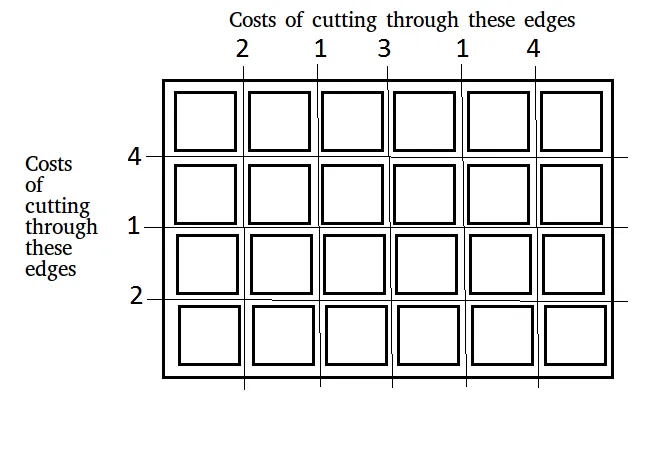
Дана дошка розмірів n × m який потрібно розрізати на n × m квадратів. Вартість виконання різу по горизонтальній або вертикальній кромці надається в двох масивах:

• x[] : Скорочення витрат уздовж вертикальних країв (по довжині).
• і [] : Скорочення витрат уздовж горизонтальних країв (по ширині).

Знайдіть мінімальну загальну вартість, необхідну для оптимального розрізання дошки на квадрати.

приклади: 

введення: x[] = [2 1 3 1 4] y[] = [4 1 2] n = 4 m = 6
Вихід: 42
Пояснення:

Спочатку ні. горизонтальних сегментів = 1 & немає. вертикальних відрізків = 1.
Оптимальний спосіб нарізки на квадрат:
Виберіть 4 (з x) -> вертикальний розріз Вартість = 4 × горизонтальні сегменти = 4
 Тепер горизонтальні сегменти = 1 вертикальні сегменти = 2.
Виберіть 4 (від y) -> горизонтальний розріз Вартість = 4 × вертикальні сегменти = 8
 Тепер горизонтальні сегменти = 2 вертикальні сегменти = 2.
Виберіть 3 (з x) -> вертикальний розріз Вартість = 3 × горизонтальні сегменти = 6
 Тепер горизонтальні сегменти = 2 вертикальні сегменти = 3.
Виберіть 2 (з x) -> вертикальний розріз Вартість = 2 × горизонтальні сегменти = 4
 Тепер горизонтальні сегменти = 2 вертикальні сегменти = 4.
Виберіть 2 (з y) -> горизонтальний розріз Вартість = 2 × вертикальні сегменти = 8
 Тепер горизонтальні сегменти = 3 вертикальні сегменти = 4.
Виберіть 1 (з x) -> вертикальний розріз Вартість = 1 × горизонтальні сегменти = 3
Тепер горизонтальні сегменти = 3 вертикальні сегменти = 5.
Виберіть 1 (з x) -> вертикальний розріз Вартість = 1 × горизонтальні сегменти = 3
Тепер горизонтальні сегменти = 3 вертикальні сегменти = 6.
Виберіть 1 (з y) -> горизонтальний розріз Вартість = 1 × вертикальні сегменти = 6
Тепер горизонтальні сегменти = 4 вертикальні сегменти = 6.
Отже, загальна вартість = 4 + 8 + 6 + 4 + 8 + 3 + 3 + 6 = 42.

введення: x[] = [1 1 1] y[] = [1 1 1] n = 4 m = 4
Вихід: 15
Пояснення:
Спочатку ні. горизонтальних сегментів = 1 & немає. вертикальних відрізків = 1.
Оптимальний спосіб нарізки на квадрат:
Виберіть 1 (з y) -> горизонтальний розріз Вартість = 1 × вертикальні сегменти = 1
Тепер горизонтальні сегменти = 2 вертикальні сегменти = 1.
Виберіть 1 (з y) -> горизонтальний розріз Вартість = 1 × вертикальні сегменти = 1
Тепер горизонтальні сегменти = 3 вертикальні сегменти = 1.
Виберіть 1 (з y) -> горизонтальний розріз Вартість = 1 × вертикальні сегменти = 1
Тепер горизонтальні сегменти = 4 вертикальні сегменти = 1.
Виберіть 1 (з x) -> вертикальний розріз Вартість = 1 × горизонтальні сегменти = 4
Тепер горизонтальні сегменти = 4 вертикальні сегменти = 2.
Виберіть 1 (з x) -> вертикальний розріз Вартість = 1 × горизонтальні сегменти = 4
Тепер горизонтальні сегменти = 4 вертикальні сегменти = 3.
Виберіть 1 (з x) -> вертикальний розріз Вартість = 1 × горизонтальні сегменти = 4
Тепер горизонтальні сегменти = 4 вертикальні сегменти = 4
Отже, загальна вартість = 1 + 1 + 1 + 4 + 4 + 4 = 15.

Зміст

• [Наївний підхід] Спробуйте всі перестановки - O((n+m)!×(n+m)) часу та O(n+m) простору
• [Очікуваний підхід] Використання жадібної техніки - O( n (log n)+m (log m)) час і O(1) простір

[Наївний підхід] Спробуйте всі перестановки - O((n+m)!×(n+m)) часу та O(n+m) простору

Ідея полягає в тому, щоб створити всі можливі перестановки заданих розрізів, а потім обчислити вартість для кожної перестановки. Нарешті поверніть мінімальну вартість серед них.

Примітка: Цей підхід неможливий для більших вхідних даних, оскільки кількість перестановок факторіально зростає як (m+n-2)!.
Для кожної перестановки ми повинні обчислити вартість за O(m+n) часу. Отже, загальна часова складність стає O((m+n−2)!×(m+n)).

[Очікуваний підхід] Використання жадібної техніки - O( n (log n)+m (log m)) час і O(1) простір

Ідея полягає в тому, щоб спочатку зробити найдорожчі розрізи за допомогою a жадібний підхід . Спостереження полягає в тому, що вибір найвищого зниження витрат на кожному кроці зменшує майбутні витрати, впливаючи на кілька частин одночасно. Ми сортуємо витрати на вертикальне (x) і горизонтальне (y) скорочення в порядку спадання, а потім послідовно обираємо більший, щоб максимізувати економію. Решта розрізів обробляються окремо, щоб усі секції були оптимально розділені.

Що відбувається, коли ми робимо розріз?

• Горизонтальний зріз → ви ріжете по ширині, тому кількість горизонтальних смуг збільшується (hCount++). Але вартість множиться на vCount (кількість вертикальних смуг), оскільки горизонтальний розріз має проходити через усі вертикальні сегменти.
• Вертикальний зріз → ви ріжете по висоті, тому кількість вертикальних смуг збільшується (vCount++). Але вартість множиться на hCount (кількість горизонтальних смуг), оскільки вертикальний розріз має проходити через усі горизонтальні сегменти.

Кроки вирішення проблеми:

• Відсортуйте масиви x і y в порядку спадання.
• Використовуйте два вказівники, один для x і інший для y, починаючи від найбільшого значення та рухаючись до менших значень.
• Підтримуйте hCount і vCount , щоб відстежувати, скільки сегментів впливає кожен розріз, і оновлювати їх відповідно.
• Повторюйте поки x і y мають необроблені розрізи, завжди вибираючи більшу вартість, щоб мінімізувати загальні витрати.
• Якщо x залишилося розрізів, обробіть їх за допомогою множника hCount ; аналогічно обробіть решту y розрізів за допомогою vCount.
• Накопичуйте загальну вартість на кожному кроці за формулою: знижена вартість * кількість уражених частин, що забезпечує мінімальну вартість.

#include   #include #include   using namespace std; int minCost(int n int m   vector<int>& x vector<int>& y) {    // Sort the cutting costs in ascending order  sort(x.begin() x.end());  sort(y.begin() y.end());   int hCount = 1 vCount = 1;   int i = x.size() - 1 j = y.size() - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } int main() {    int n = 4 m = 6;  vector<int> x = {2 1 3 1 4};  vector<int> y = {4 1 2};  cout << minCost(n m x y) << endl;  return 0; } 

import java.util.Arrays; class GfG {    static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Arrays.sort(x);  Arrays.sort(y);   int hCount = 1 vCount = 1;   int i = x.length - 1 j = y.length - 1;   int totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;   vCount++;  i--;  }   else {  totalCost += y[j] * vCount;   hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }  public static void main(String[] args) {    int n = 4m = 6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  System.out.println(minCost(n m x y));  } } 

def minCost(nm x y): # Sort the cutting costs in ascending order x.sort() y.sort() hCount vCount = 1 1 i j = len(x) - 1 len(y) - 1 totalCost = 0 while i >= 0 and j >= 0: # Choose the larger cost cut to  # minimize future costs if x[i] >= y[j]: totalCost += x[i] * hCount vCount += 1 i -= 1 else: totalCost += y[j] * vCount hCount += 1 j -= 1 # Process remaining vertical cuts while i >= 0: totalCost += x[i] * hCount vCount += 1 i -= 1 # Process remaining horizontal cuts while j >= 0: totalCost += y[j] * vCount hCount += 1 j -= 1 return totalCost if __name__ == '__main__': nm = 4 6 x = [2 1 3 1 4] y = [4 1 2] print(minCost(nmx y)) 

using System; class GfG {  public static int minCost(int n int m   int[] x int[] y) {    // Sort the cutting costs in ascending order  Array.Sort(x);  Array.Sort(y);  int hCount = 1 vCount = 1;  int i = x.Length - 1 j = y.Length - 1;  int totalCost = 0;  // Process the cuts in greedy manner  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost;  }    public static void Main() {    int n=4m=6;  int[] x = {2 1 3 1 4};  int[] y = {4 1 2};  Console.WriteLine(minCost(nm x y));  } } 

function minCost( nm x y) {    // Sort the cutting costs in ascending order  x.sort((a b) => a - b);  y.sort((a b) => a - b);  let hCount = 1 vCount = 1;  let i = x.length - 1 j = y.length - 1;  let totalCost = 0;  while (i >= 0 && j >= 0) {    // Choose the larger cost cut to   // minimize future costs  if (x[i] >= y[j]) {  totalCost += x[i] * hCount;  vCount++;  i--;  }   else {  totalCost += y[j] * vCount;  hCount++;  j--;  }  }  // Process remaining vertical cuts  while (i >= 0) {  totalCost += x[i] * hCount;  vCount++;  i--;  }  // Process remaining horizontal cuts  while (j >= 0) {  totalCost += y[j] * vCount;  hCount++;  j--;  }  return totalCost; } // Driver Code let n = 4m = 6; let x = [2 1 3 1 4]; let y = [4 1 2]; console.log(minCost(nm x y)); 

42