Дано два рядки, S1 і S2 , завдання полягає в тому, щоб знайти довжину найдовшої спільної підпослідовності, тобто найдовшої підпослідовності в обох рядках.

А найдовша спільна підпослідовність (LCS) визначається як найдовша підпослідовність, яка є спільною для всіх даних вхідних послідовностей.

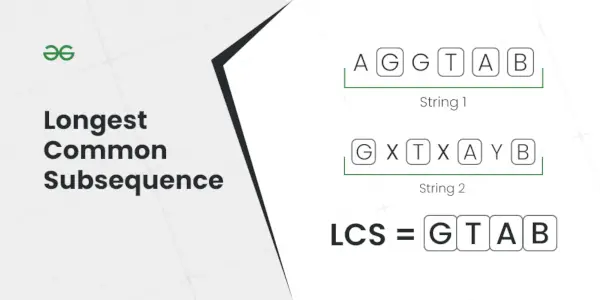
Найдовша загальна підпослідовність

приклади:

введення: S1 = ABC, S2 = ACD
Вихід: 2
Пояснення: Найдовшою підпослідовністю, яка присутня в обох рядках, є AC.

введення: S1 = AGGTAB, S2 = GXTXAYB
Вихід: 4
Пояснення: Найдовшою спільною підпослідовністю є GTAB.

c програми

введення: S1 = ABC, S2 = CBA
Вихід: 1
Пояснення: Існує три загальні підпослідовності довжиною 1, A, B і C, і немає спільної підпослідовності довжини більше 1.

введення: S1 = XYZW, S2 = XYWZ
Вихід: 3
Пояснення: Існує дві загальні підпослідовності довжиною 3 XYZ і XYW, і немає спільної підпослідовності. довжиною більше 3.

Найдовша загальна підпослідовність (LCS) з використанням рекурсії:

Згенеруйте всі можливі підпослідовності та знайдіть серед них найдовшу, яка присутня в обох рядках, використовуючи Для реалізації ідеї виконайте наступні кроки:

• Створіть рекурсивну функцію [скажімо lcs() ].
• Перевірте співвідношення між першими символами рядків, які ще не оброблені.
  • Залежно від відношення виклик наступної рекурсивної функції, як зазначено вище.
• Повертає довжину LCS, отриману як відповідь.

Нижче наведено реалізацію рекурсивного підходу:

C++

// A Naive recursive implementation of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], Y[0..n-1] int lcs(string X, string Y, int m, int n)  // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; } // This code is contributed by rathbhupendra>

C

// A Naive recursive implementation // of LCS problem #include  int max(int a, int b); // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int i, int j)  // Utility function to get max of // 2 integers int max(int a, int b) { return (a>б) ? а : б; } // Код драйвера int main() { char S1[] = 'BD';  char S2[] = 'ABCD';  int m = strlen(S1);  int n = strlen(S2);  int i = 0, j = 0;  // Виклик функції printf('Довжина LCS становить %d', lcs(S1, S2, i, j));  повернути 0; }>

Java

// A Naive recursive implementation of LCS problem in java import java.io.*; import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)   n == 0)  return 0;  if (X.charAt(m - 1) == Y.charAt(n - 1))  return 1 + lcs(X, Y, m - 1, n - 1);  else  return max(lcs(X, Y, m, n - 1),  lcs(X, Y, m - 1, n));    // Utility function to get max of 2 integers  int max(int a, int b) { return (a>б) ? а : б; } // Код драйвера public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  Рядок S1 = 'AGGTAB';  Рядок S2 = 'GXTXAYB';  int m = S1.length();  int n = S2.length();  System.out.println('Довжина LCS становить' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Цей код надав Сакет Кумар>

Python

# A Naive recursive Python implementation of LCS problem def lcs(X, Y, m, n): if m == 0 or n == 0: return 0 elif X[m-1] == Y[n-1]: return 1 + lcs(X, Y, m-1, n-1) else: return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)) # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' print('Length of LCS is', lcs(S1, S2, len(S1), len(S2)))>

C#

// C# Naive recursive implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)    if (m == 0   // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>б) ? а : б; } // Код драйвера public static void Main() { String S1 = 'AGGTAB';  Рядок S2 = 'GXTXAYB';  int m = S1.Length;  int n = S2.Length;  Console.Write('Довжина LCS становить' + ' ' + lcs(S1, S2, m, n));  } } // Цей код надав Sam007>

Javascript

>

PHP

 // A Naive recursive PHP  // implementation of LCS problem  function lcs($X, $Y, $m, $n)  $n == 0) return 0; else if ($X[$m - 1] == $Y[$n - 1]) return 1 + lcs($X, $Y, $m - 1, $n - 1); else return max(lcs($X, $Y, $m, $n - 1), lcs($X, $Y, $m - 1, $n));  // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; echo 'Length of LCS is '; echo lcs($S1 , $S2, strlen($S1), strlen($S2)); // This code is contributed  // by Shivi_Aggarwal  ?>>

Вихід

Length of LCS is 4>

Часова складність: O(2^m+n)
Допоміжний простір: О(1)

Використання найдовшої спільної підпослідовності (LCS). Запам'ятовування :

Якщо ми уважно звернемо увагу, ми можемо помітити, що наведене вище рекурсивне рішення має такі дві властивості:

1. Оптимальна підструктура:

Див. для розв’язання структури L(X[0, 1, . . ., m-1], Y[0, 1, . . . , n-1]) ми використовуємо підструктури X[0 , 1, …, m-2], Y[0, 1,…, n-2] залежно від ситуації (тобто використовуючи їх оптимально), щоб знайти розв’язок цілого.

2. Перекриваються підпроблеми:

Якщо ми використовуємо наведений вище рекурсивний підхід для рядків BD і А Б В Г , ми отримаємо часткове дерево рекурсії, як показано нижче. Тут ми бачимо, що підзадача L(BD, ABCD) обчислюється більше одного разу. Якщо розглядати загальне дерево, то буде декілька таких перекриваючих підпроблем.

L(AXYT, AYZX)
/
L(AXY, AYZX) L(AXYT, AYZ)
/ /
L(AX, AYZX) L(AXY, AYZ) L(AXY, AYZ) L(AXYT, AY)

для циклів java

Підхід: Завдяки наявності цих двох властивостей ми можемо використовувати динамічне програмування або мемоізацію для вирішення проблеми. Нижче наведено підхід до вирішення за допомогою рекурсії.

• Створіть рекурсивну функцію. Також створіть 2D-масив для зберігання результату унікального стану.
• Під час виклику рекурсії, якщо той самий стан викликається більше одного разу, ми можемо безпосередньо повернути відповідь, збережену для цього стану, замість повторного обчислення.

Нижче наведено реалізацію вищезазначеного підходу:

C++

// A Top-Down DP implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(char* X, char* Y, int m, int n,  vector>& dp) { if (m == 0 || n == 0) повертає 0;  if (X[m - 1] == Y[n - 1]) return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) { return dp[m][n];  } return dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)); } // Код драйвера int main() { char X[] = 'AGGTAB';  char Y[] = 'GXTXAYB';  int m = strlen(X);  int n = strlen(Y);  вектор> dp(m + 1, вектор (n + 1, -1));  cout<< 'Length of LCS is ' << lcs(X, Y, m, n, dp);  return 0; }>

Java

/*package whatever //do not write package name here */ import java.io.*; class GFG {  // A Top-Down DP implementation of LCS problem  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n,  int[][] dp)  {  if (m == 0 || n == 0)  return 0;  if (dp[m][n] != -1)  return dp[m][n];  if (X.charAt(m - 1) == Y.charAt(n - 1)) {  dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  return dp[m][n];  }  dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp));  return dp[m][n];  }  // Drivers code  public static void main(String args[])  {  String X = 'AGGTAB';  String Y = 'GXTXAYB';  int m = X.length();  int n = Y.length();  int[][] dp = new int[m + 1][n + 1];  for (int i = 0; i < m + 1; i++) {  for (int j = 0; j < n + 1; j++) {  dp[i][j] = -1;  }  }  System.out.println('Length of LCS is '  + lcs(X, Y, m, n, dp));  } } // This code is contributed by shinjanpatra>

Python

# A Top-Down DP implementation of LCS problem # Returns length of LCS for X[0..m-1], Y[0..n-1] def lcs(X, Y, m, n, dp): if (m == 0 or n == 0): return 0 if (dp[m][n] != -1): return dp[m][n] if X[m - 1] == Y[n - 1]: dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp) return dp[m][n] dp[m][n] = max(lcs(X, Y, m, n - 1, dp), lcs(X, Y, m - 1, n, dp)) return dp[m][n] # Driver code X = 'AGGTAB' Y = 'GXTXAYB' m = len(X) n = len(Y) dp = [[-1 for i in range(n + 1)]for j in range(m + 1)] print(f'Length of LCS is {lcs(X, Y, m, n, dp)}') # This code is contributed by shinjanpatra>

C#

/* C# Naive recursive implementation of LCS problem */ using System; class GFG {  /* Returns length of LCS for X[0..m-1], Y[0..n-1] */  static int lcs(char[] X, char[] Y, int m, int n,  int[, ] L)  {  if (m == 0 || n == 0)  return 0;  if (L[m, n] != -1)  return L[m, n];  if (X[m - 1] == Y[n - 1]) {  L[m, n] = 1 + lcs(X, Y, m - 1, n - 1, L);  return L[m, n];  }  L[m, n] = max(lcs(X, Y, m, n - 1, L),  lcs(X, Y, m - 1, n, L));  return L[m, n];  }  /* Utility function to get max of 2 integers */  static int max(int a, int b) { return (a>б) ? а : б; } public static void Main() { String s1 = 'AGGTAB';  Рядок s2 = 'GXTXAYB';  char[] X = s1.ToCharArray();  char[] Y = s2.ToCharArray();  int m = X.Length;  int n = Y.Length;  int[,] L = новий int[m + 1, n + 1];  для (int i = 0; i<= m; i++) {  for (int j = 0; j <= n; j++) {  L[i, j] = -1;  }  }  Console.Write('Length of LCS is'  + ' ' + lcs(X, Y, m, n, L));  } } // This code is contributed by akshitsaxenaa09>

Javascript

/* A Top-Down DP implementation of LCS problem */ /* Returns length of LCS for X[0..m-1], Y[0..n-1] */ function lcs(X, Y, m, n, dp) {  if (m == 0 || n == 0)  return 0;  if (X[m - 1] == Y[n - 1])  return dp[m][n] = 1 + lcs(X, Y, m - 1, n - 1, dp);  if (dp[m][n] != -1) {  return dp[m][n];  }  return dp[m][n] = Math.max(lcs(X, Y, m, n - 1, dp),  lcs(X, Y, m - 1, n, dp)); } /* Driver code */ let X = 'AGGTAB'; let Y = 'GXTXAYB'; let m = X.length; let n = Y.length; let dp = new Array(m + 1); for(let i = 0; i < m + 1; i++) {  dp[i] = new Array(n + 1).fill(-1); }  console.log('Length of LCS is ' + lcs(X, Y, m, n, dp)); // This code is contributed by shinjanpatra>

Вихід

Length of LCS is 4>

Часова складність: O(m * n), де m і n — довжини рядків.
Допоміжний простір: O(m * n) Тут рекурсивний стековий простір ігнорується.

Найдовша загальна підпослідовність (LCS) з використанням «знизу вгору» (табуляція):

Ми можемо використати наступні кроки, щоб реалізувати підхід динамічного програмування для LCS.

• Створіть 2D масив dp[][] з рядками та стовпцями, що дорівнюють довжині кожного вхідного рядка плюс 1 [кількість рядків вказує на індекси S1 а в стовпцях вказуються індекси о S2 ].
• Ініціалізуйте перший рядок і стовпець масиву dp на 0.
• Перебирайте рядки масиву dp, починаючи з 1 (скажімо, використовуючи ітератор i ).
  • Для кожного i , повторити всі стовпці з j = від 1 до n :
    • Якщо S1[i-1] дорівнює S2[j-1] , встановіть для поточного елемента масиву dp значення елемента ( dp[i-1][j-1] + 1 ).
    • Інакше встановіть для поточного елемента масиву dp максимальне значення dp[i-1][j] і dp[i][j-1] .
• Після вкладених циклів останній елемент масиву dp міститиме довжину LCS.

Перегляньте наведену нижче ілюстрацію для кращого розуміння:

Ілюстрація:

список java в масив

Скажіть, що струни є S1 = AGGTAB і S2 = GXTXAYB .

Перший крок: Спочатку створіть двовимірну матрицю (скажімо, dp[][]) розміром 8 x 7, перший рядок і перший стовпець якої заповнені 0.

Створення таблиці dp

Другий крок: Перехід для i = 1. Коли j стає 5, S1[0] і S2[4] рівні. Отже, dp[][] оновлено. Для інших елементів візьміть максимум dp[i-1][j] і dp[i][j-1]. (У цьому випадку, якщо обидва значення рівні, ми використали стрілки до попередніх рядків).

Заповнення рядка №1

пекло зворотного виклику в javascript

Третій крок: Під час обходу для i = 2 S1[1] і S2[0] однакові (обидва є «G»). Отже, значення dp у цій клітинці оновлюється. Решта елементів оновлюється відповідно до умов.

Заповнення рядка № 2

Четвертий крок: Для i = 3 S1[2] і S2[0] знову однакові. Оновлення такі.

Ряд заповнення № 3

П'ятий крок: Для i = 4 ми бачимо, що S1[3] і S2[2] однакові. Отже, dp[4][3] оновлено як dp[3][2] + 1 = 2.

Заповнення ряду 4

Шостий крок: Тут ми бачимо, що для i = 5 і j = 5 значення S1[4] і S2[4] однакові (тобто обидва є «A»). Отже, dp[5][5] оновлюється відповідним чином і стає 3.

зробити сценарій оболонки виконуваним

Заповнення ряду 5

Останній крок: Для i = 6 подивіться, що останні символи обох рядків однакові (вони «B»). Тому значення dp[6][7] стає 4.

Заповнення останнього ряду

Отже, ми отримуємо максимальну довжину загальної підпослідовності як 4 .

Нижче наведено табличну реалізацію проблеми LCS.

C++

// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; // Returns length of LCS for X[0..m-1], // Y[0..n-1] int lcs(string X, string Y, int m, int n) {  // Initializing a matrix of size  // (m+1)*(n+1)  int L[m + 1][n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion. Note that  // L[i][j] contains length of LCS of  // X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)   if (i == 0   }  // L[m][n] contains length of LCS  // for X[0..n-1] and Y[0..m-1]  return L[m][n]; } // Driver code int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  int m = S1.size();  int n = S2.size();  // Function call  cout << 'Length of LCS is ' << lcs(S1, S2, m, n);  return 0; }>

Java

// Dynamic Programming Java implementation of LCS problem import java.util.*; public class LongestCommonSubsequence {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  int lcs(String X, String Y, int m, int n)  {  int L[][] = new int[m + 1][n + 1];  // Following steps build L[m+1][n+1] in bottom up  // fashion. Note that L[i][j] contains length of LCS  // of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i][j] = 0;  else if (X.charAt(i - 1) == Y.charAt(j - 1))  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }  return L[m][n];  }  // Utility function to get max of 2 integers  int max(int a, int b) { return (a>б) ? а : б; } public static void main(String[] args) { LongestCommonSubsequence lcs = new LongestCommonSubsequence();  Рядок S1 = 'AGGTAB';  Рядок S2 = 'GXTXAYB';  int m = S1.length();  int n = S2.length();  System.out.println('Довжина LCS становить' + ' ' + lcs.lcs(S1, S2, m, n));  } } // Цей код надав Сакет Кумар>

Python

# Dynamic Programming implementation of LCS problem def lcs(X, Y, m, n): # Declaring the array for storing the dp values L = [[None]*(n+1) for i in range(m+1)] # Following steps build L[m+1][n+1] in bottom up fashion # Note: L[i][j] contains length of LCS of X[0..i-1] # and Y[0..j-1] for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: L[i][j] = 0 elif X[i-1] == Y[j-1]: L[i][j] = L[i-1][j-1]+1 else: L[i][j] = max(L[i-1][j], L[i][j-1]) # L[m][n] contains the length of LCS of X[0..n-1] & Y[0..m-1] return L[m][n] # Driver code if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' m = len(S1) n = len(S2) print('Length of LCS is', lcs(S1, S2, m, n)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

C#

// Dynamic Programming implementation of LCS problem using System; class GFG {  // Returns length of LCS for X[0..m-1], Y[0..n-1]  static int lcs(String X, String Y, int m, int n)  {  int[, ] L = new int[m + 1, n + 1];  // Following steps build L[m+1][n+1]  // in bottom up fashion.  // Note that L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1]  for (int i = 0; i <= m; i++) {  for (int j = 0; j <= n; j++)  j == 0)  L[i, j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i, j] = L[i - 1, j - 1] + 1;  else  L[i, j] = max(L[i - 1, j], L[i, j - 1]);    }  return L[m, n];  }  // Utility function to get max of 2 integers  static int max(int a, int b) { return (a>б) ? а : б; } // Код драйвера public static void Main() { String S1 = 'AGGTAB';  Рядок S2 = 'GXTXAYB';  int m = S1.Length;  int n = S2.Length;  Console.Write('Довжина LCS становить' + ' ' + lcs(S1, S2, m, n));  } } // Цей код надав Sam007>

Javascript

// Dynamic Programming Java implementation of LCS problem // Utility function to get max of 2 integers  function max(a, b) {  if (a>б) повернути а;  інакше повертає b; } // Повертає довжину LCS для X[0..m-1], Y[0..n-1] function lcs(X, Y, m, n) { var L = new Array(m + 1);  for(vari i = 0; i< L.length; i++)   {  L[i] = new Array(n + 1);  }  var i, j;    /* Following steps build L[m+1][n+1] in  bottom up fashion. Note that L[i][j]  contains length of LCS of X[0..i-1]  and Y[0..j-1] */  for(i = 0; i <= m; i++)  {  for(j = 0; j <= n; j++)   j == 0)  L[i][j] = 0;  else if (X[i - 1] == Y[j - 1])  L[i][j] = L[i - 1][j - 1] + 1;  else  L[i][j] = max(L[i - 1][j], L[i][j - 1]);    }    /* L[m][n] contains length of LCS  for X[0..n-1] and Y[0..m-1] */  return L[m][n]; } // Driver code var S1 = 'AGGTAB'; var S2 = 'GXTXAYB'; var m = S1.length; var n = S2.length; console.log('Length of LCS is ' + lcs(S1, S2, m, n)); // This code is contributed by akshitsaxenaa09>

PHP

 // Dynamic Programming C#  // implementation of LCS problem  function lcs($X , $Y, $m, $n) { // Following steps build L[m+1][n+1]  // in bottom up fashion .  // Note: L[i][j] contains length of  // LCS of X[0..i-1] and Y[0..j-1] for ($i = 0; $i <= $m; $i++) { for ($j = 0; $j <= $n; $j++)  if ($i == 0  } // L[m][n] contains the length of  // LCS of X[0..n-1] & Y[0..m-1]  return $L[$m][$n]; } // Driver Code  $S1 = 'AGGTAB'; $S2 = 'GXTXAYB'; $m = strlen($S1); $n = strlen($S2) ; echo 'Length of LCS is '; echo lcs($S1, $S2, $m, $n); // This code is contributed  // by Shivi_Aggarwal  ?>>

Вихід

Length of LCS is 4>

Часова складність: O(m * n), що набагато краще, ніж найгірша часова складність реалізації Naive Recursive.
Допоміжний простір: O(m * n), тому що алгоритм використовує масив розміром (m+1)*(n+1) для зберігання довжини загальних підрядків.

Найдовша загальна підпослідовність (LCS) з використанням Bottom-Up (Space-Optimization):

• У наведеному вище підході до таблиці ми використовуємо L[i-1][j] і L[i][j] тощо, тут L[i-1] посилатиметься на попередній рядок матриці L, а L[i] посилатиметься на поточний рядок.
• Ми можемо оптимізувати простір, використовуючи два вектори: один попередній, а інший поточний.
• Коли внутрішній цикл for виходить, ми ініціалізуємо попередній рівний поточному.

Нижче наведено реалізацію:

C++

// Dynamic Programming C++ implementation // of LCS problem #include  using namespace std; int longestCommonSubsequence(string& text1, string& text2) {  int n = text1.size();  int m = text2.size();  // initializing 2 vectors of size m  vector prev(m + 1, 0), cur(m + 1, 0);  для (int idx2 = 0; idx2< m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2]  = 0 + max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m]; } int main() {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  cout << 'Length of LCS is '  << longestCommonSubsequence(S1, S2);  return 0; }>

Java

// Dynamic Programming Java implementation of LCS problem import java.util.Arrays; public class GFG {  public static int longestCommonSubsequence(String text1, String text2) {  int n = text1.length();  int m = text2.length();  // Initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx1 = 1; idx1 < n + 1; idx1++) {  for (int idx2 = 1; idx2 < m + 1; idx2++) {  // If matching  if (text1.charAt(idx1 - 1) == text2.charAt(idx2 - 1))  cur[idx2] = 1 + prev[idx2 - 1];  // Not matching  else  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  prev = Arrays.copyOf(cur, m + 1);  }  return cur[m];  }  public static void main(String[] args) {  String S1 = 'AGGTAB';  String S2 = 'GXTXAYB';  // Function call  System.out.println('Length of LCS is ' + longestCommonSubsequence(S1, S2));  } }>

Python

def longestCommonSubsequence(text1, text2): n = len(text1) m = len(text2) # Initializing two lists of size m prev = [0] * (m + 1) cur = [0] * (m + 1) for idx1 in range(1, n + 1): for idx2 in range(1, m + 1): # If characters are matching if text1[idx1 - 1] == text2[idx2 - 1]: cur[idx2] = 1 + prev[idx2 - 1] else: # If characters are not matching cur[idx2] = max(cur[idx2 - 1], prev[idx2]) prev = cur.copy() return cur[m] if __name__ == '__main__': S1 = 'AGGTAB' S2 = 'GXTXAYB' # Function call print('Length of LCS is', longestCommonSubsequence(S1, S2)) # This code is contributed by Rishabh Mathur>

C#

using System; class Program {  static int LongestCommonSubsequence(string text1, string text2)  {  int n = text1.Length;  int m = text2.Length;  // initializing 2 arrays of size m  int[] prev = new int[m + 1];  int[] cur = new int[m + 1];  for (int idx2 = 0; idx2 < m + 1; idx2++)  cur[idx2] = 0;  for (int idx1 = 1; idx1 < n + 1; idx1++)  {  for (int idx2 = 1; idx2 < m + 1; idx2++)  {  // if matching  if (text1[idx1 - 1] == text2[idx2 - 1])  cur[idx2] = 1 + prev[idx2 - 1];  // not matching  else  cur[idx2] = 0 + Math.Max(cur[idx2 - 1], prev[idx2]);  }  prev = cur;  }  return cur[m];  }  static void Main()  {  string S1 = 'AGGTAB';  string S2 = 'GXTXAYB';  // Function call  Console.WriteLine('Length of LCS is ' + LongestCommonSubsequence(S1, S2));  } }>

Javascript

function longestCommonSubsequence(text1, text2) {  const n = text1.length;  const m = text2.length;  // Initializing two arrays of size m  let prev = new Array(m + 1).fill(0);  let cur = new Array(m + 1).fill(0);  for (let idx2 = 0; idx2 < m + 1; idx2++) {  cur[idx2] = 0;  }  for (let idx1 = 1; idx1 < n + 1; idx1++) {  for (let idx2 = 1; idx2 < m + 1; idx2++) {  // If characters match  if (text1[idx1 - 1] === text2[idx2 - 1]) {  cur[idx2] = 1 + prev[idx2 - 1];  }  // If characters don't match  else {  cur[idx2] = Math.max(cur[idx2 - 1], prev[idx2]);  }  }  // Update the 'prev' array  prev = [...cur];  }  return cur[m]; } // Main function function main() {  const S1 = 'AGGTAB';  const S2 = 'GXTXAYB';  // Function call  console.log('Length of LCS is ' + longestCommonSubsequence(S1, S2)); } // Call the main function main();>

Вихід

Length of LCS is 4>

Часова складність: O(m * n), яка залишається незмінною.
Допоміжний простір: O(m), тому що алгоритм використовує два масиви розміром m.