Лінійна регресія та логістична регресія — це два відомі алгоритми машинного навчання, які підпадають під контрольовану техніку навчання. Оскільки обидва алгоритми мають контрольований характер, отже, ці алгоритми використовують позначений набір даних для прогнозування. Але головна відмінність між ними полягає в тому, як вони використовуються. Лінійна регресія використовується для вирішення задач регресії, тоді як логістична регресія використовується для вирішення задач класифікації. Нижче наведено опис обох алгоритмів разом із таблицею відмінностей.
Лінійна регресія:
- Лінійна регресія — це один із найпростіших алгоритмів машинного навчання, який відноситься до техніки керованого навчання та використовується для вирішення проблем регресії.
- Він використовується для прогнозування безперервної залежної змінної за допомогою незалежних змінних.
- Метою лінійної регресії є знаходження найкращої відповідної лінії, яка може точно передбачити результат для безперервної залежної змінної.
- Якщо для прогнозування використовується одна незалежна змінна, то це називається простою лінійною регресією, а якщо існує більше двох незалежних змінних, то така регресія називається множинною лінійною регресією.
- Знаходячи лінію найкращого підходу, алгоритм встановлює зв’язок між залежною змінною та незалежною змінною. І зв'язок має бути лінійним.
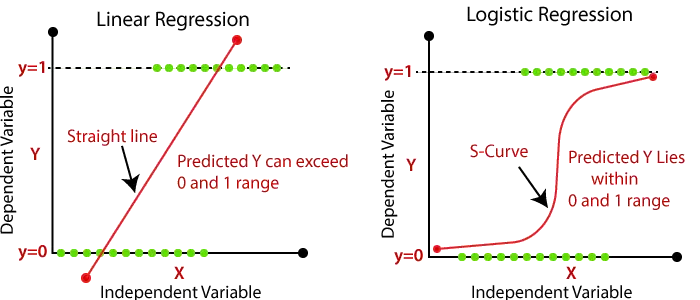
- Результатом для лінійної регресії мають бути лише безперервні значення, такі як ціна, вік, зарплата тощо. Зв’язок між залежною змінною та незалежною змінною можна показати на зображенні нижче:

На зображенні вище залежна змінна розташована на осі Y (зарплата), а незалежна змінна – на осі абсцис (досвід). Лінію регресії можна записати так:
y= a<sub>0</sub>+a<sub>1</sub>x+ ε
Де0і а1– коефіцієнти, а ε – похибка.
Логістична регресія:
- Логістична регресія є одним із найпопулярніших алгоритмів машинного навчання, який відноситься до методів навчання під керівництвом.
- Його можна використовувати як для задач класифікації, так і для задач регресії, але в основному використовується для задач класифікації.
- Логістична регресія використовується для прогнозування категоріальної залежної змінної за допомогою незалежних змінних.
- Результат задачі логістичної регресії може бути лише між 0 і 1.
- Логістичну регресію можна використовувати, коли потрібні ймовірності між двома класами. Наприклад, чи буде сьогодні дощ чи ні, 0 чи 1, істина чи хибність тощо.
- Логістична регресія базується на концепції оцінки максимальної правдоподібності. Відповідно до цієї оцінки, спостережувані дані повинні бути найбільш вірогідними.
- У логістичній регресії ми пропускаємо зважену суму вхідних даних через функцію активації, яка може відображати значення від 0 до 1. Така функція активації відома як сигмовидна функція і отримана крива називається сигмоподібною кривою або S-кривою. Розгляньте зображення нижче:

- Рівняння логістичної регресії таке:

Різниця між лінійною регресією та логістичною регресією:
| Лінійна регресія | Логістична регресія |
|---|---|
| Лінійна регресія використовується для прогнозування безперервної залежної змінної з використанням заданого набору незалежних змінних. | Логістична регресія використовується для прогнозування категоріальної залежної змінної за допомогою даного набору незалежних змінних. |
| Лінійна регресія використовується для вирішення задачі регресії. | Логістична регресія використовується для вирішення завдань класифікації. |
| У лінійній регресії ми прогнозуємо значення неперервних змінних. | У логістичній регресії ми прогнозуємо значення категоріальних змінних. |
| У лінійній регресії ми знаходимо лінію найкращого підходу, за якою ми можемо легко передбачити результат. | У логістичній регресії ми знаходимо S-криву, за якою ми можемо класифікувати вибірки. |
| Для оцінки точності використовується метод найменших квадратів. | Для оцінки точності використовується метод максимальної правдоподібності. |
| Результатом лінійної регресії має бути безперервне значення, наприклад ціна, вік тощо. | Результатом логістичної регресії має бути категоріальне значення, наприклад 0 або 1, Так або Ні тощо. |
| У лінійній регресії вимагається, щоб зв’язок між залежною змінною та незалежною змінною був лінійним. | У логістичній регресії не вимагається наявність лінійного зв’язку між залежною та незалежною змінними. |
| У лінійній регресії може бути колінеарність між незалежними змінними. | У логістичній регресії не повинно бути колінеарності між незалежною змінною. |
