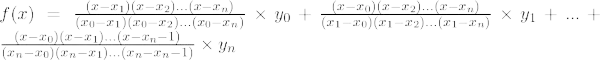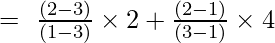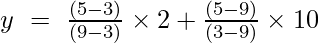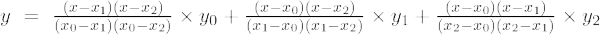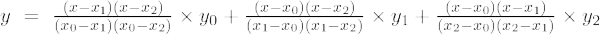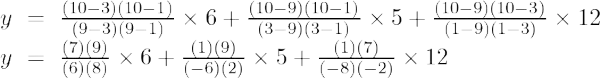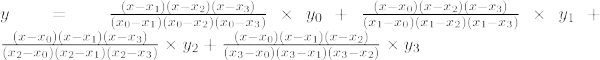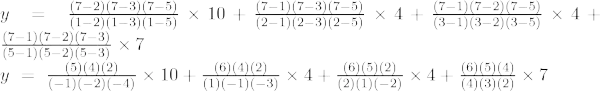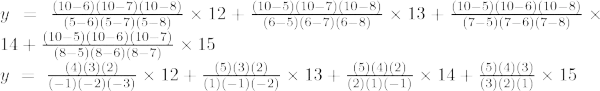logo

TechCodeview

Формула інтерполяції Лагранжа

Формула інтерполяції Лагранжа знаходить поліном, званий поліномом Лагранжа, який приймає певні значення в довільній точці. Це n-й ступінь поліноміальний вираз функції f(x). Метод інтерполяції використовується для пошуку нових точок даних у діапазоні дискретного набору відомих точок даних.

У цій статті ми детально дізнаємося про інтерполяцію Лагранжа, формулу інтерполяції Лагранжа, доказ формули інтерполяції Лагранжа, приклади на основі формули інтерполяції Лагранжа та інші.



Що таке інтерполяція Лагранжа?

Інтерполяція Лагранжа — це спосіб знаходження значення будь-якої функції в будь-якій заданій точці, коли функція не задана. Ми використовуємо інші точки функції, щоб отримати значення функції в будь-якій необхідній точці.

Припустимо, що ми маємо функцію y = f(x), у якій заміна значень x дає різні значення y. І нам дають дві точки (х1, і1) і (x2, і2) на кривій, тоді значення y при x = a (константа) обчислюється за допомогою формули інтерполяції Лагранжа.

Формула інтерполяції Лагранжа

Дано кілька дійсних значень x1, х2, х3, …, хпі у1, і2, і3, … іпі буде поліном P з дійсними коефіцієнтами, що задовольняють умови P(xi) = іi, ∀ i = {1, 2, 3, …, n} і ступінь полінома P має бути меншим за кількість дійсних значень, тобто ступінь (P)



Формула інтерполяції Лагранжа для n-го порядку

Інтерполяційна формула Лагранжа для nтисполіном ступеня наведено нижче:

Інтерполяційна формула Лагранжа для n тис порядок є,

f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} imes y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)} imes y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n



Інтерполяційна формула Лагранжа першого порядку

Якщо Степінь полінома дорівнює 1, тому його називають поліномом першого порядку. Інтерполяційна формула Лагранжа для 1вулполіноми порядку є,

f(x)~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

Інтерполяційна формула Лагранжа другого порядку

Якщо ступінь полінома дорівнює 2, то він називається поліномом другого порядку. Формула інтерполяції Лагранжа для поліномів 2-го порядку:

f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

Доведення теореми Лагранжа

Розглянемо поліном n-го ступеня заданого вигляду,

f(x) = A0(x – x1)(x – x2)(x – x3)…(x – xп) + А1(x – x1)(x – x2)(x – x3)…(x – xп) + … + А(n-1)(x – x1)(x – x2)(x – x3)…(x – xп)

Підставте спостереження xiотримати Аi

Покладіть x = x0тоді ми отримуємо А0

f(x0) = і0= А0(х0– х1)(x0– х2)(x0– х3)…(x0– хп)

А 0 = і 0 /(x 0 – х 1 )(x 0 – х 2 )(x 0 – х 3 )…(x 0 – х п )

Підставляючи x = x1отримуємо А1

sql вибрати як

f(x1) = і1= А1(х1– х0)(x1– х2)(x1– х3)…(x1– хп)

А 1 = і 1 /(x 1 – х 0 )(x 1 – х 2 )(x 1 – х 3 )…(x 1 – х п )

Аналогічно, замінивши x = xпотримуємо Ап

f(xп) = іп= Ап(хп– х0)(xп– х1)(xп– х2)…(xп– хn-1)

А п = і п /(x п – х 0 )(x п – х 1 )(x п – х 2 )…(x п – х n-1 )

Якщо підставити всі значення Аiу функції f(x), де i = 1, 2, 3, …n, тоді ми отримуємо формулу інтерполяції Лагранжа як,

f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} помножити на y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)}рази на y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n

Властивості інтерполяційної формули Лагранжа

Різні властивості формули інтерполяції Лагранжа обговорюються нижче,

  • Ця формула використовується для знаходження значення функції в будь-якій точці, навіть якщо сама функція не задана.
  • Він використовується, навіть якщо наведені точки розташовані нерівномірно.
  • Він дає значення залежної змінної для будь-якої незалежної змінної, що належить до будь-якої функції, і тому використовується в числовому аналізі для знаходження значень функції тощо.

Використання формули інтерполяції Лагранжа

Різні способи використання формули інтерполяції Лагранжа обговорюються нижче,

  • Він використовується для знаходження значення залежної змінної для будь-якої окремої незалежної змінної, навіть якщо сама функція не задана.
  • Використовується для масштабування зображення.
  • Він використовується в моделюванні ШІ.
  • Використовується для навчання НЛП тощо.

Детальніше,

  • Формула інтерполяції
  • Формула лінійної інтерполяції

Приклади використання формули інтерполяції Лагранжа

Давайте розглянемо кілька прикладів запитань щодо формули інтерполяції Лагранжа.

Приклад 1: Знайдіть значення y при x = 2 для заданого набору точок (1, 2), (3, 4)

рішення:

враховуючи,

  • (х0, і0) = (1, 2)
  • (х1, і1) = (3, 4)

Інтерполяційна формула Лагранжа першого порядку:

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

При х = 2

і =~frac{(2-3)}{(1-3)}рази 2+frac{(2-1)}{(3-1)}рази 4

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Значення y при x = 2 дорівнює 3

Приклад 2: Знайдіть значення y при x = 5 для заданого набору точок (9, 2), (3, 10)

рішення:

враховуючи,

  • (х0, і0) = (9, 2)
  • (х1, і1) = (3, 10)

Інтерполяційна формула Лагранжа першого порядку:

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

При х = 5

y~=~frac{(5-3)}{(9-3)} imes 2+frac{(5-9)}{(3-9)} imes 10

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Значення y при x = 5 дорівнює 7,33

Приклад 3: Знайдіть значення y при x = 1 для заданого набору точок (1, 6), (3, 4), (2, 5)

рішення:

враховуючи,

  • (х0, і0) = (1, 6)
  • (х1, і1) = (3, 4)
  • (х2, і2) = (2, 5)

Формула інтерполяції Лагранжа другого порядку:

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

При x = 1

y~=~frac{(1-3)(1-2)}{(1-3)(1-2)} imes 6+frac{(1-1)(1-2)}{( 3-1)(3-2)} imes 4+frac{(1-1)(1-3)}{(2-1)(2-3)} imes 5 y~=~ frac{(-2)(-1)}{(-2)(-1)} imes 6+frac{(0)(-1)}{(2)(1)} imes 4+frac {(0)(-2)}{(1)(-1)}рази 5

y = (12/2) + 0 + 0

y = 6

Значення y при x = 1 дорівнює 6

Приклад 4: Знайдіть значення y при x = 10 для заданого набору точок (9, 6), (3, 5), (1, 12)

рішення:

враховуючи,

  • (х0, і0) = (9, 6)
  • (х1, і1) = (3, 5)
  • (х2, і2) = (1, 12)

Формула інтерполяції Лагранжа другого порядку:

y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} imes y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)} imes y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} imes y_2

При х = 10

y~=~frac{(10-3)(10-1)}{(9-3)(9-1)} imes 6+frac{(10-9)(10-1)}{( 3-9)(3-1)} imes 5+frac{(10-9)(10-3)}{(1-9)(1-3)} imes 12 y~=~ frac{(7)(9)}{(6)(8)} imes 6+frac{(1)(9)}{(-6)(2)} imes 5+frac{(1) (7)}{(-8)(-2)}рази 12

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Значення y при x = 10 дорівнює 9,375

Приклад 5: Знайдіть значення y при x = 7 для заданого набору точок (1, 10), (2, 4), (3, 4), (5, 7)

рішення:

враховуючи,

  • (х0, і0) = (1, 10)
  • (х1, і1) = (2, 4)
  • (х2, і2) = (3, 4)
  • (х3, і3) = (5, 7)

Інтерполяційна формула Лагранжа третього порядку:

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)}рази y_3

При х = 7

y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)}рази 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)}рази 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)} imes 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)} imes 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)} imes 10+ frac{(6)(4)(2)}{(1)(-1)(-3)} imes 4+frac{(6)(5)(2)}{(2)(1) (-2)} imes 4+frac{(6)(5)(4)}{(4)(3)(2)} imes 7

y = -50 + 64 – 60 + 35

y = 99 – 110 = -одинадцять

Значення y при x = 7 дорівнює -11

Приклад 6: Знайдіть значення y при x = 10 для заданого набору точок (5, 12), (6, 13), (7, 14), (8, 15)

рішення:

враховуючи,

  • (х0, і0) = (5, 12)
  • (х1, і1) = (6, 13)
  • (х2, і2) = (7, 14)
  • (х3, і3) = (8, 15)

Інтерполяційна формула Лагранжа третього порядку:

y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)} imes y_0+frac{(x-x_0) )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)} imes y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1) )(x_3-x_2)}рази y_3

При x = 10,

y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)}разів 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)}разів 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)} imes 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)} imes 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)} imes 12+ frac{(5)(3)(2)}{(1)(-1)(-2)} imes 13+frac{(5)(4)(2)}{(2)(1) (-1)} imes 14+frac{(5)(4)(3)}{(3)(2)(1)} imes 15

y = -48 + 195 – 280 + 150

y = 17

Значення y при x = 10 дорівнює 17

списки в java

Приклад 7: Знайдіть значення y при x = 0 для заданого набору точок (-2, 5), (1, 7)

рішення:

враховуючи,

  • (х0, і0) = (-2, 5)
  • (х1, і1) = (1, 7)

Інтерполяційна формула Лагранжа першого порядку:

y~=~frac{(x-x_1)}{(x_0-x_1)} imes y_0+frac{(x-x_0)}{(x_1-x_0)} imes y_1

При x = 0,

y~=~frac{(0-1)}{(-2-1)} imes 5+frac{(0+2)}{(1+2)} imes 7

y = (5/3) + (14/3)

y = 19/3 = 6,33

Значення y при x = 0 дорівнює 6,33

Поширені запитання щодо формули інтерполяції Лагранжа

1. Що таке інтерполяційна формула Лагранжа?

Формула інтерполяції Лагранжа — це формула, яка використовується для знаходження значення залежної змінної функції для будь-якої незалежної змінної, навіть якщо сама функція не задана.

2. Які застосування формули інтерполяції Лагранжа?

Формула Лагранжа має різноманітне застосування в сучасній математиці та науках про дані,

  • Він використовується для навчання моделі AI.
  • Він використовується в обробці зображень.
  • Він використовується для побудови тривимірних та вищих кривих тощо.

3. Що таке інтерполяційна формула Лагранжа першого порядку?

Інтерполяційна формула Лагранжа першого порядку:

f(x) = (x – x 1 )/(x 0 – х 1 )×f 0 + (x – x 0 )/(x 1 – х 0 )×f 1

4. Що таке інтерполяційна формула Лагранжа другого порядку?

Інтерполяційна формула Лагранжа другого порядку:

f(x) = [(x – x 1 )(x – x 2 )/(x 0 – х 1 )(x 0 – х 2 )]×f 0 + [(x – x 0 )(x – x 2 )/(x 1 – х 0 )(x 1 – х 2 )]×f 1 + [(x – x 0 )(x – x 1 )/(x 2 – х 0 )(x 2 – х 2 )]×f 0