Двійкове дерево пошуку це структура даних, яка використовується в інформатиці для організації та зберігання даних у відсортований спосіб. Двійкове дерево пошуку відповідає всім властивостям бінарного дерева та його зліва дочірній вузол містить значення, менші за батьківський вузол і правильно дочірній вузол містить значення, більші за батьківський вузол. Ця ієрархічна структура дозволяє ефективно Пошук , Вставка , і Видалення операції над даними, що зберігаються в дереві.
тернарний оператор java
Двійкове дерево пошуку
Зміст
- Що таке бінарне дерево пошуку?
- Властивості бінарного дерева пошуку
- Обробка повторюваних значень у бінарному дереві пошуку
- Операції, що виконуються на BST
- Застосування BST
- Переваги
- Недоліки
- FAQ (часті запитання) щодо бінарного дерева пошуку:
Що таке бінарне дерево пошуку?
Двійкове дерево пошуку (BST) є особливим видом бінарне дерево у якому лівий дочірній елемент вузла має значення, менше за значення вузла, а правий дочірній елемент має значення, що перевищує значення вузла. Ця властивість називається властивістю BST і дає змогу ефективно шукати, вставляти та видаляти елементи в дереві.
Властивості бінарного дерева пошуку:
- Ліве піддерево вузла містить лише вузли з ключами, меншими за ключ вузла.
- Праве піддерево вузла містить лише вузли з ключами, більшими за ключ вузла.
- Це означає, що все ліворуч від кореня менше значення кореня, а все праворуч від кореня більше значення кореня. Завдяки такій роботі двійковий пошук дуже простий.
- Кожне з лівого та правого піддерев також має бути бінарним деревом пошуку.
- Не повинно бути повторюваних вузлів (BST може мати повторювані значення з різними підходами до обробки)
Обробка повторюваних значень у бінарному дереві пошуку:
- Ми повинні дотримуватися послідовного процесу, тобто або зберігати повторюване значення ліворуч, або зберігати повторюване значення праворуч від кореня, але дотримуйтеся свого підходу.
Основні операції над бінарним деревом пошуку:
1. Пошук вузла в BST:
Пошук у BST означає знайти певний вузол у структурі даних. У бінарному дереві пошуку пошук вузла простий через його певний порядок. Етапи пошуку вузла в дереві бінарного пошуку перераховані наступним чином –
- Спочатку порівняйте елемент, який потрібно шукати, з кореневим елементом дерева.
- Якщо кореневий елемент збігається з цільовим елементом, повертається розташування вузла.
- Якщо він не збігається, то перевірте, чи елемент менший за кореневий елемент, якщо він менший за кореневий елемент, то перейдіть до лівого піддерева.
- Якщо він більший за кореневий елемент, то перейдіть до правого піддерева.
- Повторюйте описану вище процедуру рекурсивно, доки не буде знайдено збіг.
- Якщо елемент не знайдено або відсутній у дереві, повертається NULL.
Тепер давайте розберемося з пошуком у бінарному дереві на прикладі:
Нижче подано BST, і ми повинні шукати елемент 6.
код:
Нижче наведено реалізацію пошуку в BST:
C++ // C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->ключ = елемент; temp->left = temp->right = NULL; зворотна температура; } // Допоміжна функція для вставки // нового вузла з заданим ключем у BST struct node* insert(struct node* node, int key) { // Якщо дерево порожнє, повертає новий вузол if (node == NULL) ) повертає новий вузол (ключ); // Інакше, повторити вниз по дереву, якщо (ключ< node->ключ) node->left = вставити(node->left, key); інакше якщо (ключ> вузол->ключ) вузол->правий = вставити(вузол->правий, ключ); // Повертає (незмінений) покажчик вузла return node; } // Службова функція для пошуку ключа в BST struct node* search(struct node* root, int key) root->key == key) return root; // Ключ більший за ключ root, якщо (root->key< key) return search(root->справа, ключ); // Ключ менший за ключ кореня return search(root->left, key);> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->ключ = елемент; temp->left = temp->right = NULL; зворотна температура; } // Допоміжна функція для вставки // нового вузла з заданим ключем у BST struct node* insert(struct node* node, int key) { // Якщо дерево порожнє, повертає новий вузол if (node == NULL) ) повертає новий вузол (ключ); // Інакше, повторити вниз по дереву, якщо (ключ< node->ключ) node->left = вставити(node->left, key); інакше якщо (ключ> вузол->ключ) вузол->правий = вставити(вузол->правий, ключ); // Повертає (незмінений) покажчик вузла return node; } // Допоміжна функція для пошуку ключа в BST struct node* search(struct node* root, int key)> Java // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>node.key) node.right = вставити(node.right, ключ); // Повертає (незмінений) покажчик вузла return node; } // Допоміжна функція для пошуку ключа в BST Node search(Node root, int key) // Базові випадки: root має значення null або ключ присутній у root if (root == null> Python # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Повертає (незмінений) покажчик вузла return node # Допоміжна функція для пошуку ключа в BST def search(root, key): # Базові випадки: root is null або ключ присутній у root, якщо root має значення None або root.key == ключ: повернути root # Ключ більший за ключ root, якщо root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
JavaScript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Повертає (незмінений) покажчик вузла return node; } // Допоміжна функція для пошуку ключа у функції BST search(root, key) { // Базові випадки: root має значення null або ключ присутній у root if (root === null || root.key === key ) { повернути корінь; } // Ключ більший за ключ root, якщо (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
bash для циклу
2. Вставте вузол у BST :
Новий ключ завжди вставляється на аркуші. Почніть пошук ключа від кореня до кінцевого вузла. Після того, як кінцевий вузол знайдено, новий вузол додається як дочірній елемент листового вузла.
код:
Нижче наведено реалізацію вставки окремого вузла в бінарне дерево пошуку:
C++ // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ключ = елемент; temp->left = temp->right = NULL; зворотна температура; } // Функція для вставки нового вузла з // заданим ключем у BST struct node* insert(struct node* node, int key) { // Якщо дерево порожнє, повертає новий вузол if (node == NULL) return newNode(ключ); // Інакше, повторити вниз по дереву, якщо (ключ< node->ключ) { node->left = insert(node->left, key); } else if (ключ> вузол->ключ) { вузол->правий = вставити(вузол->правий, ключ); } // Повертає покажчик вузла return node; }> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ключ = елемент; temp->left = temp->right = NULL; зворотна температура; } // Функція для вставки нового вузла з // заданим ключем у BST struct node* insert(struct node* node, int key) { // Якщо дерево порожнє, повертає новий вузол if (node == NULL) return newNode(ключ); // Інакше, повторити вниз по дереву, якщо (ключ< node->ключ) { node->left = insert(node->left, key); } else if (ключ> вузол->ключ) { вузол->правий = вставити(вузол->правий, ключ); } // Повертає покажчик вузла return node; }> Java class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Повернення вузла return node; } }> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Повернути покажчик вузла return node>
Javascript // Given Node Structure class Node { constructor(key){ this.key = key; this.left = null; this.right = null; } } // Function to insert a new node with // given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node == null) return new Node(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Повертає покажчик вузла return node; }> Часова складність: O(N), де N - кількість вузлів BST
Допоміжний простір: О(1)
3. Видалити вузол BST :
Він використовується для видалення вузла з певним ключем із BST і повернення нового BST.
Різні сценарії видалення вузла:
Вузол, який потрібно видалити, є кінцевим вузлом :
Це просто, ви можете просто обнулити його.
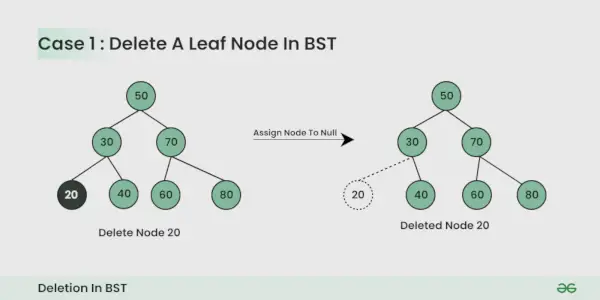
Вузол, який потрібно видалити, має одного дочірнього елемента :
Ви можете просто замінити вузол дочірнім вузлом.
міста в австралії
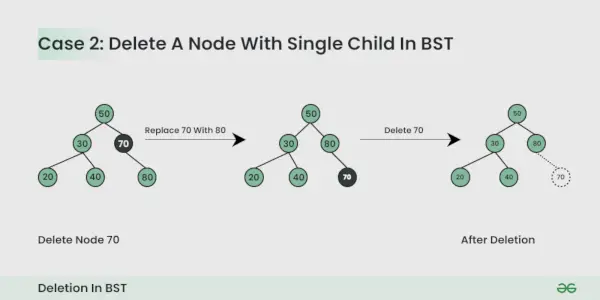
Вузол, який потрібно видалити, має двох дочірніх елементів :
Тут ми повинні видалити вузол таким чином, щоб результуюче дерево відповідало властивостям BST. Хитрість полягає в тому, щоб знайти порядкового наступника вузла. Скопіюйте вміст наступника inorder до вузла та видаліть наступника inorder.
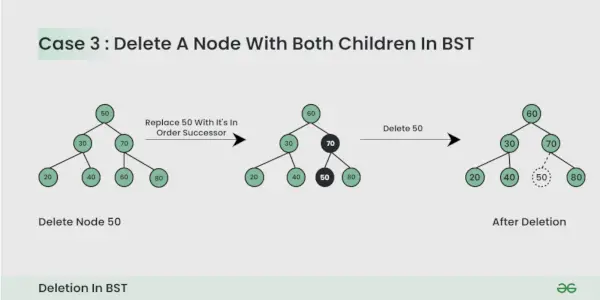
Під час видалення вузла BST подбайте про наступне:
- Необхідно розібратися, яка буде заміна видаляється вузла.
- Хочете мінімально порушити існуючу структуру дерева
- Може взяти вузол заміни з видалених вузлів лівого або правого піддерева.
- Якщо взяти if з лівого піддерева, ми повинні взяти найбільше значення в лівому піддереві.
- Якщо взяти if з правого піддерева, ми повинні взяти найменше значення в правому піддереві.
код:
Нижче наведено реалізацію видалення в BST:
oracle sql не дорівнюєC++
// C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ключ = елемент; temp->left = temp->right = NULL; зворотна температура; } // Функція для вставки нового вузла з // заданим ключем у BST struct node* insert(struct node* node, int key) { // Якщо дерево порожнє, повертає новий вузол if (node == NULL) return newNode(ключ); // Інакше, повторити вниз по дереву, якщо (ключ< node->ключ) { node->left = insert(node->left, key); } else if (ключ> вузол->ключ) { вузол->правий = вставити(вузол->правий, ключ); } // Повертає покажчик вузла return node; } // Функція, яка повертає вузол із мінімальним // значенням ключа, знайденим у цьому дереві struct node* minValueNode(struct node* node) { struct node* current = node; // Цикл вниз, щоб знайти крайній лівий аркуш while (current && current->left != NULL) current = current->left; зворотний струм; } // Функція, яка видаляє ключ і // повертає новий кореневий struct node* deleteNode(struct node* root, int key) { // базовий випадок if (root == NULL) return root; // Якщо ключ, який потрібно видалити, // менший за кореневий ключ, // він знаходиться в лівому піддереві, якщо (ключ< root->ключ) { root->left = deleteNode(root->left, key); } // Якщо ключ, який потрібно видалити, // більший за ключ кореня, // він знаходиться в правому піддереві else if (key> root->key) { root->right = deleteNode(root-> справа, ключ); } // Якщо ключ збігається з ключем кореня, // тоді цей вузол // буде видалено else { // Вузол лише з одним дочірнім елементом // або без дочірнього, якщо (root->left == NULL) { struct node* temp = root->right; вільний (корінь); зворотна температура; } else if (root->right == NULL) { struct node* temp = root->left; вільний (корінь); зворотна температура; } // Вузол із двома дочірніми елементами: // Отримує наступник у порядку (найменший // у правому піддереві) struct node* temp = minValueNode(root->right); // Скопіюйте вміст наступника за порядком // до цього вузла root->key = temp->key; // Видалити спадкоємця в порядку root->right = deleteNode(root->right, temp->key); } повернути корінь; }> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ключ = елемент; temp->left = temp->right = NULL; зворотна температура; } // Функція для вставки нового вузла з // заданим ключем у BST struct node* insert(struct node* node, int key) { // Якщо дерево порожнє, повертає новий вузол if (node == NULL) return newNode(ключ); // Інакше, повторити вниз по дереву, якщо (ключ< node->ключ) { node->left = insert(node->left, key); } else if (ключ> вузол->ключ) { вузол->правий = вставити(вузол->правий, ключ); } // Повертає покажчик вузла return node; } // Функція, яка повертає вузол із мінімальним // значенням ключа, знайденим у цьому дереві struct node* minValueNode(struct node* node) { struct node* current = node; // Цикл вниз, щоб знайти крайній лівий аркуш while (current && current->left != NULL) current = current->left; зворотний струм; } // Функція, яка видаляє ключ і // повертає новий кореневий struct node* deleteNode(struct node* root, int key) { // базовий випадок if (root == NULL) return root; // Якщо ключ, який потрібно видалити, // менший за кореневий ключ, // він знаходиться в лівому піддереві, якщо (ключ< root->ключ) { root->left = deleteNode(root->left, key); } // Якщо ключ, який потрібно видалити, // більший за ключ кореня, // він знаходиться в правому піддереві else if (key> root->key) { root->right = deleteNode(root-> справа, ключ); } // Якщо ключ збігається з ключем кореня, // тоді цей вузол // буде видалено else { // Вузол лише з одним дочірнім елементом // або без дочірнього, якщо (root->left == NULL) { struct node* temp = root->right; вільний (корінь); зворотна температура; } else if (root->right == NULL) { struct node* temp = root->left; вільний (корінь); зворотна температура; } // Вузол із двома дочірніми елементами: // Отримує наступник у порядку (найменший // у правому піддереві) struct node* temp = minValueNode(root->right); // Скопіюйте вміст наступника за порядком // до цього вузла root->key = temp->key; // Видалити спадкоємця в порядку root->right = deleteNode(root->right, temp->key); } повернути корінь; }> Java // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Повернення вузла return node; } // Функція, яка повертає вузол із мінімальним // значенням ключа, знайденим у цьому дереві static node minValueNode(node node) { node current = node; // Цикл вниз, щоб знайти крайній лівий аркуш while (current != null && current.left != null) current = current.left; зворотний струм; } // Функція, яка видаляє ключ і // повертає новий кореневий статичний вузол deleteNode(node root, int key) { // базовий випадок if (root == null) return root; // Якщо ключ, який потрібно видалити, // менший за кореневий ключ, // він знаходиться в лівому піддереві, якщо (ключ< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>root.key) { root.right = deleteNode(root.right, key); } // Якщо ключ збігається з ключем кореня, // тоді цей вузол // буде видалено else { // Вузол лише з одним дочірнім елементом // або без дочірнього if (root.left == null) { node temp = root.right; зворотна температура; } else if (root.right == null) { node temp = root.left; зворотна температура; } // Вузол із двома дочірніми елементами: // Отримує наступник у порядку (найменший // у правому піддереві) node temp = minValueNode(root.right); // Скопіюйте вміст наступника за порядком // до цього вузла root.key = temp.key; // Видалити спадкоємця в порядку root.right = deleteNode(root.right, temp.key); } повернути корінь; }> Python # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Повертає вказівник вузла return root # Функція для обходу BST за порядком визначення inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Функція, яка повертає вузол із мінімальним # значенням ключа, знайденим у цьому дереві def minValueNode(node): current = node # Перейдіть униз, щоб знайти крайній лівий аркуш під час поточного та current.left не є None: current = current.left return current # Функція, яка видаляє ключ і # повертає новий кореневий def deleteNode(root, key): # базовий випадок, якщо root дорівнює None: return root # Якщо ключ має бути видалений # менший за кореневий ключ, # тоді він лежить у лівому піддереві, якщо ключ< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # Якщо ключ збігається з ключем root, # тоді цей вузол # буде видалено else: # Вузол лише з одним дочірнім # або без дочірнього if root.left is None: temp = root.right root = None return temp elif root.right is None: temp = root.left root = None return temp # Вузол із двома дочірніми елементами: # Отримати наступника за порядком (найменший # у праве піддерево) temp = minValueNode(root.right) # Скопіювати вміст наступника за порядком # до цього вузла root.key = temp.key # Видалити наступник за порядком root.right = deleteNode(root.right, temp.key) повернути корінь>>> 4. Traversal (обхід у порядку BST) :
У випадку бінарних дерев пошуку (BST) обхід за порядком дає вузли в порядку неспадання. Спочатку відвідуємо лівий дочірній, потім корінь, а потім правий дочірній.
Нижче наведено реалізацію того, як виконати впорядкований обхід бінарного дерева пошуку:
C++ключ; inorder(корінь->справа); } } // Код драйвера int main() { /* Давайте створимо наступний BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Створення кореня BST = insert(root, 50); вставити (корінь, 30); вставити (корінь, 20); вставити (корінь, 40); вставити (корінь, 70); вставити (корінь, 60); вставити (корінь, 80); // Виклик функції inorder(root); повернути 0; } // Цей код створено shivanisinghss2110>
C // C program to implement // inorder traversal of BST #include #include // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ключ = елемент; temp->left = temp->right = NULL; зворотна температура; } // Функція для вставки нового вузла з // заданим ключем у BST struct node* insert(struct node* node, int key) { // Якщо дерево порожнє, повертає новий вузол if (node == NULL) return newNode(ключ); // Інакше, повторити вниз по дереву, якщо (ключ< node->ключ) { node->left = insert(node->left, key); } else if (ключ> вузол->ключ) { вузол->правий = вставити(вузол->правий, ключ); } // Повертає покажчик вузла return node; } // Функція для обходу BST за порядком void inorder(struct node* root) { if (root != NULL) { inorder(root->left); printf('%d ', корінь->ключ); inorder(корінь->справа); } } // Код драйвера int main() { /* Давайте створимо наступний BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Створення кореня BST = insert(root, 50); вставити (корінь, 30); вставити (корінь, 20); вставити (корінь, 40); вставити (корінь, 70); вставити (корінь, 60); вставити (корінь, 80); // Виклик функції inorder(root); повернути 0; }> Java import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>node.key) { node.right = insert(node.right, key); } // Повернення вузла return node; } // Функція для обходу за порядком BST static void inorder(node root) { if (root != null) { inorder(root.left); System.out.print(' ' + root.key); inorder(root.right); } } // Код драйвера public static void main(String[] args) { /* Давайте створимо наступний BST 50 / 30 70 / / 20 40 60 80 */ node root = null; // вставка значення 50 root = insert(root, 50); // вставка значення 30 insert(root, 30); // вставка значення 20 insert(root, 20); // вставка значення 40 insert(root, 40); // вставка значення 70 insert(root, 70); // вставка значення 60 insert(root, 60); // вставка значення 80 insert(root, 80); // надрукувати BST inorder(root); } } // Цей код створено abhijitjadhav1998> Python3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Повертає вказівник вузла return node # Функція для обходу BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Код драйвера if __name__ == '__main__': # Давайте створимо наступний BST # 50 # / # 30 70 # / / # 20 40 60 80 root = None # Створення BST root = insert(root, 50) insert(root, 30) insert(root, 20) insert(root, 40) insert(root, 70) insert(root, 60) insert(root , 80) # Виклик функції inorder(root) #Цей код створено japmeet01>
Вихід
20 30 40 50 60 70 80>
Часова складність: O(N), де N - кількість вузлів BST
Допоміжний простір: О(1)
Застосування BST:
- Алгоритми графів: BST можна використовувати для реалізації графових алгоритмів, наприклад, у алгоритмах мінімального остовного дерева.
- Пріоритетні черги: BST можна використовувати для реалізації пріоритетних черг, де елемент з найвищим пріоритетом знаходиться в корені дерева, а елементи з нижчим пріоритетом зберігаються в піддеревах.
- Самобалансуюче бінарне дерево пошуку: BST можна використовувати як самобалансуючі структури даних, такі як дерево AVL і червоно-чорне дерево.
- Зберігання та пошук даних: BST можна використовувати для швидкого зберігання та отримання даних, наприклад, у базах даних, де пошук певного запису можна виконувати за логарифмічний час.
Переваги:
- Швидкий пошук: Пошук певного значення в BST має середню часову складність O(log n), де n — кількість вузлів у дереві. Це набагато швидше, ніж пошук елемента в масиві чи зв’язаному списку, який у гіршому випадку має часову складність O(n).
- Обхід у порядку: BST можна обходити в порядку, який відвідує ліве піддерево, корінь і праве піддерево. Це можна використовувати для сортування набору даних.
- Економія простору: BST економлять простір, оскільки не зберігають надлишкової інформації, на відміну від масивів і пов’язаних списків.
Недоліки:
- Перекошені дерева: Якщо дерево стає перекошеним, часова складність операцій пошуку, вставки та видалення становитиме O(n) замість O(log n), що може зробити дерево неефективним.
- Необхідний додатковий час: Дерева з самобалансуванням вимагають додаткового часу для підтримки балансу під час операцій вставки та видалення.
- Ефективність: BST неефективні для наборів даних із великою кількістю дублікатів, оскільки вони витрачатимуть простір.
поширені запитання(Питання що часто задаються)на бінарному дереві пошуку:
1. Що таке бінарне дерево пошуку?
Двійкове дерево пошуку (BST). двійкове дерево, у якому кожен вузол лівого піддерева менший за кореневий, а кожен вузол правого піддерева має значення, більше кореневого . Властивості бінарного дерева пошуку є рекурсивними: якщо ми розглядаємо будь-який вузол як кореневий, ці властивості залишаться істинними.
2. Що таке операція бінарного дерева пошуку?
У бінарному дереві пошуку є три основні операції: 1. Вставка, 2. Видалення, 3. Пошук. Завдяки його властивостям він ефективний для пошуку будь-якого елемента в бінарному дереві пошуку.
3. Що таке бінарне дерево пошуку та дерево AVL?
Двійкове дерево пошуку : Двійкове дерево пошуку (BST) — це двійкове дерево, у якому кожен вузол у лівому піддереві менший за кореневий, а кожен вузол у правому піддереві має значення, що перевищує кореневе.
Дерево AVL : Двійкові дерева пошуку (BST), які самобалансуються та обертаються автоматично, відомі як дерева AVL.
4. Для чого використовується бінарне дерево пошуку?
Двійкові дерева пошуку можна використовувати для реалізації абстрактних типів даних, таких як динамічні набори, таблиці пошуку та черги пріоритетів, і використовується в алгоритми сортування наприклад сорт дерева.
5. Яка різниця між бінарним деревом пошуку та бінарним деревом?
Двійкове дерево пошуку — це дерево, яке дотримується певного порядку розташування елементів, тоді як двійкове дерево не дотримується жодного порядку.
масиви bash
Пов'язані статті:
- Застосування БСТ
- Застосування, переваги та недоліки бінарного дерева пошуку
- Вставка в бінарне дерево пошуку (BST)
- Пошук у бінарному дереві пошуку (BST)
- Видалення в бінарному дереві пошуку (BST)
