• Алгоритм сходження на пагорб — це алгоритм локального пошуку, який постійно рухається в напрямку збільшення висоти/значення, щоб знайти вершину гори або найкраще вирішення проблеми. Він завершується, коли досягає пікового значення, де жоден сусід не має більшого значення.
• Алгоритм сходження на пагорб – це техніка, яка використовується для оптимізації математичних задач. Одним із широко обговорюваних прикладів алгоритму підйому на пагорб є задача комівояжера, у якій нам потрібно мінімізувати відстань, яку проїжджає комівояжер.
• Його також називають жадібним локальним пошуком, оскільки він шукає лише свого доброго найближчого сусіда, а не за його межами.
• Вузол алгоритму сходження на пагорб має два компоненти: стан і значення.
• Підйом на пагорб здебільшого використовується, коли доступна хороша евристика.
• У цьому алгоритмі нам не потрібно підтримувати й обробляти дерево пошуку чи графік, оскільки він зберігає лише один поточний стан.

Особливості Hill Climbing:

Нижче наведено деякі основні функції алгоритму сходження на пагорб:

Створити та перевірити варіант:Підйом на пагорб є варіантом методу Generate and Test. Метод Generate and Test створює зворотний зв’язок, який допомагає вирішити, у якому напрямку рухатися в просторі пошуку.Жадібний підхід:Алгоритм пошуку Hill-climbing рухається в напрямку, який оптимізує вартість.Без повернення:Він не повертає назад простір пошуку, оскільки не запам’ятовує попередні стани.

Діаграма простору станів для сходження на пагорб:

Ландшафт простору станів — це графічне представлення алгоритму сходження на пагорб, яке показує графік між різними станами алгоритму та цільовою функцією/вартістю.

На осі Y ми взяли функцію, яка може бути цільовою функцією або функцією вартості, і простір станів на осі X. Якщо функція на осі Y є вартістю, тоді мета пошуку полягає в тому, щоб знайти глобальний мінімум і локальний мінімум. Якщо функція осі Y є цільовою функцією, то метою пошуку є знаходження глобального максимуму та локального максимуму.

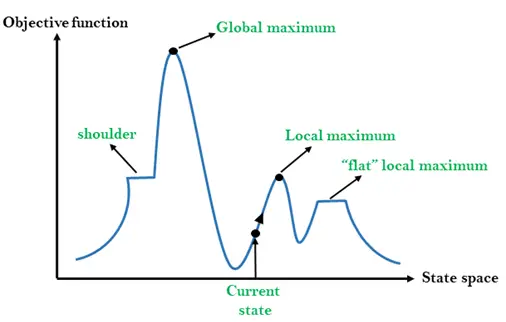
Різні регіони простору штату:

Місцевий максимум: Локальний максимум - це стан, який кращий за сусідні стани, але є також інший стан, який вищий за нього.

Глобальний максимум: Глобальний максимум – це найкращий можливий стан просторового ландшафту стану. Має найвище значення цільової функції.

Поточний стан: Це стан на ландшафтній діаграмі, де зараз присутній агент.

Плоский локальний максимум: Це плоский простір у ландшафті, де всі сусідні держави поточних держав мають однакову цінність.

Плече: Це регіон плато, який має висхідний край.

Типи алгоритму сходження на пагорб:

• Просте сходження на пагорб:
• Найкрутіший підйом на гору:
• Стохастичне сходження на пагорб:

1. Просте сходження на пагорб:

Просте сходження на пагорб — це найпростіший спосіб реалізувати алгоритм сходження на пагорб. Він лише оцінює стан сусіднього вузла за раз і вибирає перший, який оптимізує поточну вартість, і встановлює його як поточний стан . Він лише перевіряє, чи є один наступний стан, і якщо він знаходить кращий, ніж поточний стан, тоді переміщується в інший стан. Цей алгоритм має такі особливості:

• Менше часу
• Менш оптимальне рішення і рішення не гарантоване

Алгоритм простого сходження на гору:

Крок 1:Оцініть початковий стан, якщо це цільовий стан, поверніть успіх і зупиніть.Крок 2:Цикл, доки не знайдено рішення або не залишиться нового оператора для застосування.крок 3:Виберіть і застосуйте оператор до поточного стану.крок 4:Перевірте новий стан:
1. Якщо це цільовий стан, тоді поверніть успіх і вийдіть.
2. Інакше, якщо він кращий за поточний стан, тоді призначте новий стан як поточний стан.
3. Інакше, якщо не краще, ніж поточний стан, поверніться до кроку 2.
крок 5:Вихід.

2. Підйом на пагорб із найкрутішим підйомом:

Алгоритм найкрутішого підйому є різновидом простого алгоритму сходження на пагорб. Цей алгоритм перевіряє всі сусідні вузли поточного стану та вибирає один сусідній вузол, який є найближчим до цільового стану. Цей алгоритм споживає більше часу, оскільки він шукає кілька сусідів

Алгоритм підйому на пагорб із найкрутішим підйомом:

Крок 1:Оцініть початковий стан, якщо це цільовий стан, поверніть успіх і зупиніться, інакше зробіть поточний стан початковим.Крок 2:Цикл, поки не буде знайдено рішення або поточний стан не зміниться.
1. Нехай SUCC буде таким станом, що будь-який наступник нинішнього стану буде кращим за нього.
2. Для кожного оператора, який стосується поточного стану:
   1. Застосуйте новий оператор і згенеруйте новий стан.
   2. Оцініть новий стан.
   3. Якщо це цільовий стан, поверніть його та вийдіть, інакше порівняйте його з SUCC.
   4. Якщо він кращий за SUCC, тоді встановіть новий стан як SUCC.
   5. Якщо SUCC кращий за поточний стан, тоді встановіть поточний стан на SUCC.
крок 5:Вихід.

3. Стохастичний підйом на пагорб:

Стохастичний підйом на пагорб не перевіряє всіх сусідів перед тим, як рухатися. Швидше, цей алгоритм пошуку вибирає один сусідній вузол випадковим чином і вирішує, чи вибрати його як поточний стан, чи перевірити інший стан.

Проблеми в алгоритмі підйому на пагорб:

1. Місцевий максимум: Локальний максимум — це піковий стан у ландшафті, який кращий за кожен із сусідніх станів, але також присутній інший стан, вищий за локальний максимум.

рішення: Техніка бектрекінгу може бути рішенням локального максимуму в ландшафті простору стану. Створіть список перспективних шляхів, щоб алгоритм міг повернутися до простору пошуку та досліджувати інші шляхи.

2. Плато: Плато — це плоска область простору пошуку, в якій усі сусідні стани поточного стану містять однакові значення, оскільки цей алгоритм не знаходить найкращого напрямку для руху. Пошук підйому на пагорб може бути втрачений у районі плато.

рішення: Рішення для плато полягає в тому, щоб робити великі або дуже маленькі кроки під час пошуку, щоб вирішити проблему. Випадково виберіть стан, який є далеким від поточного стану, тому можливо, що алгоритм знайде область не плато.

3. Хребти: Гребінь – це особлива форма локального максимуму. Він має територію, яка вища за навколишні території, але сам має схил, і до нього неможливо дістатися одним рухом.

рішення: Використовуючи двонаправлений пошук або рухаючись у різних напрямках, ми можемо вирішити цю проблему.

Імітація відпалу:

Алгоритм підйому, який ніколи не рухається до нижчого значення, гарантовано буде неповним, оскільки він може застрягти на локальному максимумі. І якщо алгоритм застосовує випадкове блукання, переміщуючи наступника, то він може завершитися, але не буде ефективним. Імітація відпалу це алгоритм, який забезпечує як ефективність, так і повноту.

Якщо говорити механічно Відпал це процес загартування металу або скла до високої температури з подальшим поступовим охолодженням, що дозволяє металу досягти низькоенергетичного кристалічного стану. Той самий процес використовується в симульованому відпалі, коли алгоритм вибирає випадковий хід замість того, щоб вибрати найкращий. Якщо випадковий хід покращує стан, то він йде тим самим шляхом. В іншому випадку алгоритм слідує шляху, який має ймовірність менше 1, або рухається вниз і вибирає інший шлях.