Що таке гамільтонів цикл?
Гамільтонів цикл або ланцюг на графіку Г це цикл, який відвідує кожну вершину Г рівно один раз і повертається до початкової вершини.
- Якщо граф містить гамільтонів цикл, він називається Гамільтонів графік інакше це так негамільтонівський .
- Знаходження гамільтонового циклу в графі є добре відомим NP-повна задача , що означає, що не існує відомого ефективного алгоритму для її вирішення для всіх типів графіків. Однак її можна розв’язати для невеликих чи певних типів графіків.
Проблема Гамільтонового циклу має практичне застосування в різних областях, наприклад логістика, проектування мереж та інформатика .
Що таке гамільтонів шлях?
Шлях Гамільтона на графіку Г це шлях, який відвідує кожну вершину G рівно один раз і Шлях Гамільтона не потрібно повертатися до початкової вершини. Це відкритий шлях.
- Подібний до Гамільтонів цикл проблема, пошук а Шлях Гамільтона у загальному графіку також NP-повний і може бути складним завданням. Однак часто це легша проблема, ніж знайти гамільтонів цикл.
- Шляхи Гамільтона застосовуються в різних областях, наприклад пошук оптимальних маршрутів у транспортних мережах, проектування схем та дослідження теорії графів .
Постановка проблеми: Для неорієнтованого графа завдання полягає в тому, щоб визначити, чи містить граф гамільтонів цикл чи ні. Якщо він містить, то друкує шлях.
приклад:
Рекомендовано: розв’яжіть це на ПРАКТИКА спочатку, перш ніж перейти до рішення.введення: графік[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}}
Вхідний графік[][]
повна схема суматораВихід: {0, 1, 2, 4, 3, 0}.
введення: графік[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}}
Вхідний графік[][]
Вихід: Рішення не існує
Наївний алгоритм : цю проблему можна вирішити за допомогою наведеної нижче ідеї:
Згенеруйте всі можливі конфігурації вершин і надрукуйте конфігурацію, яка задовольняє задані обмеження. Буде п! (n факторіальних) конфігурацій. Таким чином, загальна часова складність цього підходу буде О (Н!).
Використання гамільтонового циклу Алгоритм зворотного відстеження :
Створіть порожній масив шляхів і додайте вершину 0 до нього. Додайте інші вершини, починаючи з вершини 1 . Перед додаванням вершини перевірте, чи є вона суміжною з раніше доданою вершиною, а не доданою. Якщо ми знайдемо таку вершину, ми додамо її як частину розв’язку. Якщо ми не знаходимо вершину, то повертаємося помилковий .
Ілюстрації:
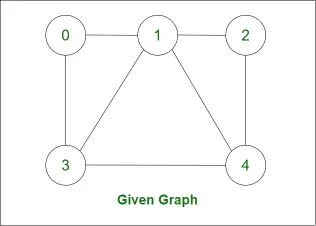
Знайдемо гамільтонів цикл для такого графіка:
- Почніть з вузла 0 .
- Застосуйте DFS для знаходження гамільтонового шляху.
- Коли досягається базовий регістр (тобто загальна кількість пройдених вузлів == V (загальна вершина) ):
- Перевірте, чи поточний вузол є сусідом початкового вузла.
- Як вузол 2 і вузол 0 не є сусідами один одного, тому повертайтеся з нього.
Починаючи з початкового вузла 0, виклик DFS
- Оскільки цикл не знайдено на шляху {0, 3, 1, 4, 2}. Отже, повернення з вузла 2, вузла 4.
- Тепер дослідіть інший варіант для вузла 1 (тобто вузла 2)
- Коли він досягне основної умови, знову перевірте наявність гамільтонового циклу
- Оскільки вузол 4 не є сусідом вузла 0, знову цикл не знайдено, а потім повертається.
- Повернення з вузла 4, вузла 2, вузла 1.
- Тепер дослідіть інші варіанти для вузла 3.
Гамільтонів цикл
- У гамільтонів шлях {0,3,4,2,1,0} ми отримуємо цикл, оскільки вузол 1 є сусідом вузла 0.
- Отже, надрукуйте цей циклічний шлях.
- Це наш гамільтонів цикл.
Нижче наведено реалізацію зворотного відстеження для пошуку гамільтонового циклу:
C++ /* C++ program for solution of Hamiltonian Cycle problem using backtracking */ #include using namespace std; // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, bool graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [path[pos - 1]][ v ] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(bool graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the // last included vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate // in Hamiltonian Cycle. We don't try for 0 as // we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added // to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ bool hamCycle(bool graph[V][V]) { int *path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false ) { cout << '
Solution does not exist'; return false; } printSolution(path); return true; } /* A utility function to print solution */ void printSolution(int path[]) { cout << 'Solution Exists:' ' Following is one Hamiltonian Cycle
'; for (int i = 0; i < V; i++) cout << path[i] << ' '; // Let us print the first vertex again // to show the complete cycle cout << path[0] << ' '; cout << endl; } // Driver Code int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ bool graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}}; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ bool graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}}; // Print the solution hamCycle(graph2); return 0; } // This is code is contributed by rathbhupendra> C++ #include using namespace std; int main() { cout << 'GFG!'; return 0; }> C /* C program for solution of Hamiltonian Cycle problem using backtracking */ #include // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ int isSafe(int v, int graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [ path[pos-1] ][ v ] == 0) return 0; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return 0; return 1; } /* A recursive utility function to solve hamiltonian cycle problem */ int hamCycleUtil(int graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included vertex to the // first vertex if ( graph[ path[pos-1] ][ path[0] ] == 1 ) return 1; else return 0; } // Try different vertices as a next candidate in Hamiltonian Cycle. // We don't try for 0 as we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos+1) == 1) return 1; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return 0; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[V][V]) { int path[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if ( hamCycleUtil(graph, path, 1) == 0 ) { printf('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { printf ('Solution Exists:' ' Following is one Hamiltonian Cycle
'); for (int i = 0; i < V; i++) printf(' %d ', path[i]); // Let us print the first vertex again to show the complete cycle printf(' %d ', path[0]); printf('
'); } // driver program to test above function int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamCycle(graph2); return 0; }> Java /* Java program for solution of Hamiltonian Cycle problem using backtracking */ class HamiltonianCycle { final int V = 5; int path[]; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ boolean isSafe(int v, int graph[][], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1]][v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ boolean hamCycleUtil(int graph[][], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[][]) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { System.out.println('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { System.out.println('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) System.out.print(' ' + path[i] + ' '); // Let us print the first vertex again to show the // complete cycle System.out.println(' ' + path[0] + ' '); } // driver program to test above function public static void main(String args[]) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code is contributed by Abhishek Shankhadhar> Python # Python program for solution of # hamiltonian cycle problem class Graph(): def __init__(self, vertices): self.graph = [[0 for column in range(vertices)] for row in range(vertices)] self.V = vertices ''' Check if this vertex is an adjacent vertex of the previously added vertex and is not included in the path earlier ''' def isSafe(self, v, pos, path): # Check if current vertex and last vertex # in path are adjacent if self.graph[ path[pos-1] ][v] == 0: return False # Check if current vertex not already in path for vertex in path: if vertex == v: return False return True # A recursive utility function to solve # hamiltonian cycle problem def hamCycleUtil(self, path, pos): # base case: if all vertices are # included in the path if pos == self.V: # Last vertex must be adjacent to the # first vertex in path to make a cycle if self.graph[ path[pos-1] ][ path[0] ] == 1: return True else: return False # Try different vertices as a next candidate # in Hamiltonian Cycle. We don't try for 0 as # we included 0 as starting point in hamCycle() for v in range(1,self.V): if self.isSafe(v, pos, path) == True: path[pos] = v if self.hamCycleUtil(path, pos+1) == True: return True # Remove current vertex if it doesn't # lead to a solution path[pos] = -1 return False def hamCycle(self): path = [-1] * self.V ''' Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected ''' path[0] = 0 if self.hamCycleUtil(path,1) == False: print ('Solution does not exist
') return False self.printSolution(path) return True def printSolution(self, path): print ('Solution Exists: Following', 'is one Hamiltonian Cycle') for vertex in path: print (vertex ) # Driver Code ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) ''' g1 = Graph(5) g1.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,],[1, 1, 0, 0, 1], [0, 1, 1, 1, 0], ] # Print the solution g1.hamCycle(); ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) ''' g2 = Graph(5) g2.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,], [1, 1, 0, 0, 0], [0, 1, 1, 0, 0], ] # Print the solution g2.hamCycle(); # This code is contributed by Divyanshu Mehta> C# // C# program for solution of Hamiltonian // Cycle problem using backtracking using System; public class HamiltonianCycle { readonly int V = 5; int []path; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, int [,]graph, int []path, int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1], v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(int [,]graph, int []path, int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1],path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int [,]graph) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { Console.WriteLine('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int []path) { Console.WriteLine('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) Console.Write(' ' + path[i] + ' '); // Let us print the first vertex again // to show the complete cycle Console.WriteLine(' ' + path[0] + ' '); } // Driver code public static void Main(String []args) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int [,]graph1= {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int [,]graph2 = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code contributed by Rajput-Ji> Javascript >
PHP // PHP program for solution of // Hamiltonian Cycle problem // using backtracking $V = 5; /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ function isSafe($v, $graph, &$path, $pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if ($graph[$path[$pos - 1]][$v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for ($i = 0; $i < $pos; $i++) if ($path[$i] == $v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ function hamCycleUtil($graph, &$path, $pos) { global $V; /* base case: If all vertices are included in Hamiltonian Cycle */ if ($pos == $V) { // And if there is an edge from the // last included vertex to the first vertex if ($graph[$path[$pos - 1]][$path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point hamCycle() for ($v = 1; $v < $V; $v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe($v, $graph, $path, $pos)) { $path[$pos] = $v; /* recur to construct rest of the path */ if (hamCycleUtil($graph, $path, $pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ $path[$pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ function hamCycle($graph) { global $V; $path = array_fill(0, $V, 0); for ($i = 0; $i < $V; $i++) $path[$i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ $path[0] = 0; if (hamCycleUtil($graph, $path, 1) == false) { echo('
Solution does not exist'); return 0; } printSolution($path); return 1; } /* A utility function to print solution */ function printSolution($path) { global $V; echo('Solution Exists: Following is '. 'one Hamiltonian Cycle
'); for ($i = 0; $i < $V; $i++) echo(' '.$path[$i].' '); // Let us print the first vertex again to show the // complete cycle echo(' '.$path[0].'
'); } // Driver Code /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ $graph1 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 1), array(0, 1, 1, 1, 0), ); // Print the solution hamCycle($graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ $graph2 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 0), array(0, 1, 1, 0, 0)); // Print the solution hamCycle($graph2); // This code is contributed by mits ?>> Вихід
Solution Exists: Following is one Hamiltonian Cycle 0 1 2 4 3 0 Solution does not exist>
Часова складність: O(N!), де N – кількість вершин.
Допоміжний простір: O(1), оскільки додатковий простір не використовується.
Примітка: Наведений вище код завжди друкує цикл, починаючи з 0 . Початкова точка не має значення, оскільки цикл можна почати з будь-якої точки. Якщо ви хочете змінити початкову точку, вам слід внести дві зміни до наведеного вище коду.
Змінити шлях[0] = 0; до path[0] = s ; де с твій новий відправна точка . Також змініть цикл for (int v = 1; v