Питання регресії та ймовірнісної класифікації можна вирішити за допомогою процесу Гаусса (GP), методики навчання під керівництвом. Оскільки кожен гаусівський процес можна розглядати як нескінченномірне узагальнення багатофакторного Розподіл Гауса , у назві з’являється термін гаусівський. У цій публікації ми обговоримо процеси Гауса для регресії, які також називають регресією процесу Гауса (GPR). Численні реальні проблеми в галузі матеріалознавства, хімії, фізики та біології були вирішені за допомогою георадара.
Зміст
лисиця чи вовк
- Регресія Гаусового процесу (GPR)
- Ключові поняття регресії процесу Гауса (GPR)
- Математична концепція регресії процесу Гауса (GPR)
- Реалізація Гаусового процесу в Python
Регресія Гаусового процесу (GPR)
Регресія процесу Гауса (GPR) — це потужний і гнучкий метод непараметричної регресії, який використовується в машинне навчання і статистика . Це особливо корисно під час вирішення проблем, пов’язаних із безперервними даними, де зв’язок між вхідними змінними та виходом явно невідомий або може бути складним. Георадар – це байєсівський підхід, який може моделювати достовірність прогнозів, що робить його цінним інструментом для різноманітних застосувань, включаючи оптимізацію, прогнозування часових рядів тощо. GPR базується на концепції гаусового процесу, який є набором випадкових величин, будь-яка кінцева кількість яких має спільний гаусівський розподіл. Процес Гауса можна розглядати як розподіл функцій.
Ключові поняття регресії процесу Гауса (GPR)
Процес Гауссена
Непараметрична ймовірнісна модель, яка називається a Гаусівський процес (GP) використовується в статистиці та машинному навчанні для регресії, класифікації та кількісного визначення невизначеності. Він зображує групу випадкових величин, кожна з яких має спільний розподіл Гаусса і може мати кінцеве число. GPs є універсальною та ефективною технікою для моделювання складних зв’язків у даних і створення прогнозів із пов’язаною невизначеністю.
Характеристика гаусових процесів :
- Непараметрична природа : лікарі загальної практики можуть пристосовуватися до складності даних, оскільки вони не покладаються на встановлену кількість параметрів моделі
- Імовірнісні прогнози : Прогнози лікарів загальної практики можна визначити кількісно, оскільки вони надають прогнози як розподіли ймовірностей.
- Інтерполяція та згладжування : GP корисні для шумних або нерегулярних даних, оскільки вони добре згладжують шумні дані та інтерполюють між точками даних.
- Маргіналізація гіперпараметрів : усуваючи вимогу щодо явного налаштування гіперпараметрів, вони маргіналізують гіперпараметри, роблячи модель простішою.
Середня функція
Прогнозне значення функції, що моделюється, у кожній вхідній точці представлено за допомогою середня функція у процесах Гауса (GP). Він функціонує як фундаментальна презумпція щодо базової структури даних. Функція середнього значення часто встановлюється на нуль за замовчуванням, необов’язково, і може бути змінена на основі властивостей даних або досвіду домену. Впливаючи на центральну тенденцію прогнозів, він допомагає лікарям загальної практики визначати закономірності чи тенденції в даних. Лікарі загальної практики надають імовірнісні прогнози, які містять невизначеність, а також точкові оцінки, включаючи функцію середнього
Коваріаційна (ядерна) функція
The коваріаційна функція , яка також називається функцією ядра, вимірює, наскільки точки вхідних даних схожі одна на одну в процесах Гауса (GP). Це важливо для характеристики поведінки моделі GP, що впливає на вибір функцій із попереднього розподілу. Функція коваріації вимірює попарну подібність, щоб визначити кореляцію між значеннями функції. GPs можуть адаптуватися до широкого діапазону шаблонів даних, від плавних трендів до складних структур, оскільки різні функції ядра вловлюють різні види кореляцій. Вибір ядра може значно вплинути на продуктивність моделі.
Попередні розподіли
The попередній розподіл , у Гаусових процесах (GP), це наше розуміння функцій до спостереження за будь-якими даними. Зазвичай вона описується коваріаційною (ядерною) функцією та середньою функцією. Тоді як коваріаційна функція описує подібність або кореляцію між значеннями функції в різних вхідних точках, середня функція кодує наші попередні очікування. Це заздалегідь використовується лікарями загальної практики для створення розподілу за функціями. У GPs попередні можуть бути обрані для представлення невизначеності даних, інтеграції знань предметної області або вказівки на гладкість.
Задні розподіли
процеси Гауса пізніше поширення показує наші переглянуті припущення щодо функцій після спостереження даних. Він об’єднує ймовірність даних із заданою функцією та попереднім розподілом. Апостеріорна регресія GP пропонує розподіл за функціями, які найбільше відповідають спостережуваним даним. Дозволяючи ймовірнісні прогнози та кількісну оцінку невизначеності, апостеріорний розподіл відображає компроміс між попередніми переконаннями, що зберігаються в попередньому розподілі, та інформацією, яку надають дані.
Математична концепція регресії процесу Гауса (GPR)
Для завдань регресії використовується непараметрична імовірнісна модель машинного навчання, яка називається регресією Гаусового процесу (GP). Це потужний інструмент для моделювання складних і неоднозначних взаємодій між вхідними та вихідними змінними. Передбачається, що багатовимірний розподіл Гауса створює точки даних у регресії GP, і мета полягає в тому, щоб зробити висновок про цей розподіл.
Регресійна модель GP має наступний математичний вираз. Припустимо x1, х2,…..,xпє точками вхідних даних, де x належать дійсним числам (-2,-1,0,1…), (xi
Припустимо, y1, і2,……., іпвихідні значення, де yiналежить дійсному числу (yi
Модель регресії GP робить припущення, що гаусівський процес із середньою функцією (
Тоді, у наборі тестових місць x*, розподіл f визначається як:
Як правило, ядерні функції використовуються для визначення середньої функції та коваріаційної функції. Як приклад, квадрат експоненційного ядра, який часто використовують, описується як:
Де,
k(x_{i}, x_{j}) = Функція ядра представлена таким чином, і вона обчислює кореляцію або подібність між двома точками вхідних даних, xiі хj.sigma^2 = Параметр дисперсії ядра такий. Він встановлює масштаб або вертикальний розкид функції ядра. Він регулює, наскільки сильно корельовані точки даних. Вищийsigma^2 дає ядерну функцію з більшою дисперсією.- exp: експоненціальна функція відповідає за піднесення e до степеня аргументу.
||x_{i} – x_{j}||^2 : різниця між точками вхідних даних, xiі хj, це квадрат евклідової відстані. Вимірюється геометрична відстань між точками в просторі ознак.- л2: це представлення масштабу довжини ядра або характерної довжини. Він регулює швидкість, з якою функція ядра погіршується, оскільки точки даних віддалені один від одного. Менший l спричиняє швидшу деградацію ядра.
Регресійна модель GP застосовує байєсівський висновок для визначення розподілу f, який, найімовірніше, створив дані з урахуванням набору навчальних даних (x, y). Для цього необхідно обчислити апостеріорний розподіл f за даними, який визначається наступним чином:
де гранична ймовірність даних дорівнює p(y|x), попередній розподіл f дорівнює p(f), а ймовірність даних за функцією f дорівнює (y|x,f).
Після вивчення апостеріорного розподілу f модель обчислює апостеріорний прогнозний розподіл, щоб робити прогнози в додаткових контрольних точках x*. Його можна визначити так:
Де,
p(f^*|x*, y, x) = Це показує умовну ймовірність прогнозованих значень функції f, враховуючи навчальні дані y та x*у новій точці введення x*Іншими словами, це розподіл ймовірностей за всіма потенційними значеннями функції на новому вхідному місці x*, залежно від спостережуваних даних y та їхніх відповідних вхідних місць x.int p(f^*|x^*, f)p(f|y,x)df = У цьому розділі рівняння використовується інтеграл для визначення умовної ймовірності. Інтеграл охоплює всі потенційні значення функції f.p(f^*|x^*, f) = Це умовний розподіл ймовірностей очікуваних значень функції f*на х*, враховуючи значення функції f у деяких проміжних місцях.p(f|y,x) = Враховуючи спостережувані дані (y) та їх вхідні місця (x), це умовний розподіл ймовірностей значень функції (f).
Для таких завдань, як прийняття рішень з урахуванням невизначеності та активне навчання, цей розподіл пропонує вимірювання невизначеності прогнозу, що може бути корисним.
Етапи регресії гаусового процесу
- Збір даних : Зберіть пари вхідних і вихідних даних для вашої проблеми регресії.
- Виберіть функцію ядра : виберіть відповідну коваріаційну функцію (ядро), яка відповідає вашій проблемі. Вибір ядра впливає на форму функцій, які може моделювати георадар.
- Оптимізація параметрів : Оцініть гіперпараметри функції ядра шляхом максимізації ймовірності даних. Це можна зробити за допомогою методів оптимізації, таких як градієнтний спуск.
- Прогноз: Отримавши нові дані, використовуйте навчену модель георадара, щоб зробити прогнози. Георадар забезпечує як прогнозоване середнє значення, так і відповідну невизначеність (дисперсію).
Впровадження регресії процесу Гауса (GPR)
Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Вихід:
У цьому коді спочатку згенеруйте кілька зразкових точок даних із додаванням шуму, потім визначте ядро RBF і створіть a Регресор процесу Гауса з цим. Модель навчається на навчальних даних і використовується для прогнозування на основі тестових даних. Нарешті, результати візуалізуються за допомогою графіка, що показує дані навчання, прогнозоване середнє значення та 95% довірчий інтервал.
Реалізація Гаусового процесу в Python
Scikit Learn
Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> Необхідні бібліотеки для Gaussian Process Regression (GPR) у Python імпортуються цим кодом; це SciPy для функцій лінійної алгебри, NumPy для числових операцій, і Matplotlib для візуалізації даних. Щоб переконатися, що він сумісний з необхідними пакетами, він додатково перевіряє версію Python і друкує її разом із версіями NumPy і scikit-learn (sklearn).
Вибір ядра
Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Вихід:
[RBF(length_scale=1),
RationalQuadratic(alpha=1, length_scale=1),
ExpSineSquared(length_scale=1, periodicity=10),
DotProduct(sigma_0=1) ** 2,
Материнська (length_scale=1, nu=1,5)]
Код визначає кількість тестових сайтів (n) та ініціалізує a випадкове насіння . Щоб відобразити вибрані ядра, він створює список із кількох функцій ядра та друкує список.
Порівняння та візуалізація ядра
Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Вихід:
RBF
gp.kernel_ RBF(length_scale=1,93)
gp.log_marginal_likelihood: -3,444937833462133
-------------------------------------------------- -
Раціональний квадратичний

gp.kernel_ RationalQuadratic(alpha=1e+05, length_scale=1,93)
gp.log_marginal_likelihood: -3,4449718909150966
--------------------------------------------------
ExpSineSquared

gp.kernel_ ExpSineSquared(length_scale=0,000524, періодичність=2,31e+04)
gp.log_marginal_likelihood: -3,4449381454930217
--------------------------------------------------
Точковий продукт

gp.kernel_ DotProduct(sigma_0=0,998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
--------------------------------------------------
Материнська

gp.kernel_ Matern(length_scale=1,99, nu=1,5)
gp.log_marginal_likelihood: -5,131637070524745
--------------------------------------------------
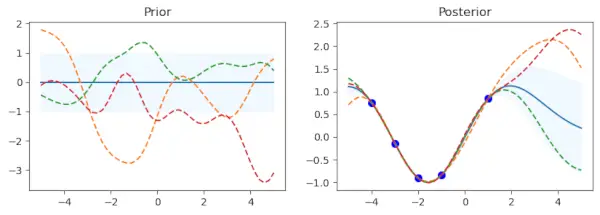
Код починається з циклу по різних функціях ядра, перелічених у списку kernel_. Гауссовий регресор процесу (gp) створюється з використанням окремого ядра для кожного ядра. Для Гаусового процесу це встановлює структуру коваріації. Щоб оцінити попередній розподіл, створюється набір тестових вхідних точок під назвою x_test зі значеннями в діапазоні від -5 до 5. Цей набір точок перетворюється на вектор-стовпець.
Використовуючи метод gp.predict, середнє значення попереднього розподілу (mu_prior) і стандартне відхилення (sd_prior) визначаються в кожній контрольній точці. Значення стандартного відхилення запитуються за допомогою параметра return_std=True. gp.sample_y (x_test, 3) використовується для отримання трьох зразків функцій із попереднього розподілу.
Перший підграф показує середнє значення попереднього розподілу, а стандартне відхилення представлено заштрихованою областю. Зразки накладаються пунктирними лініями, а середнє значення відображається суцільною лінією. Є підзаговор під назвою «Пріор». Існує визначений набір точок тренувальних даних (x_train) і цільових значень (y_train), які з ними пов’язані. Модель Гаусового процесу підбирається за допомогою цих точок (gp.fit(x_train, y_train)). П’ять точок даних із відповідними значеннями синуса складають навчальні дані в цьому коді.
Після фази підгонки навчальних даних процедура обчислює середнє значення апостеріорного розподілу (mu_post) і стандартне відхилення (sd_post) для тих самих контрольних точок (x_test). gp.sample_y(x_test, 3) також використовується для створення зразків функції з апостеріорного розподілу. Другий підграфік накладає вибіркові функції як пунктирні лінії та показує середнє значення апостеріорного розподілу, заштрихованого стандартним відхиленням. Синім кольором зображені точки тренувальних даних. Підзаговор має назву Posterior.
Щоб побачити попередній і попередній графіки для поточного ядра та отримати візуальне розуміння поведінки моделі, викличте функцію Matplotlib plt.show().
Код показує подробиці про поточне ядро, наприклад gp.kernel_, що вказує на поточне ядро, яке використовується, і gp.log_marginal_likelihood (gp.kernel_.theta), що дає журнал граничної ймовірності моделі, що використовує поточне ядро, після кожного набору попередніх і наступних графіків.
Переваги регресії процесу Гауса (GPR)
Регресія процесу Гауса (GPR) має ряд переваг у ряді застосувань:
- GPR забезпечує імовірнісну структуру для регресії, що означає, що він не лише дає точкові оцінки, але й надає оцінки невизначеності для прогнозів.
- Він дуже гнучкий і може фіксувати складні зв’язки в даних.
- Георадар може бути адаптований до різних програм, включаючи прогнозування часових рядів, оптимізацію та байєсовську оптимізацію.
Проблеми регресії процесу Гауса (GPR)
- Георадар може бути обчислювально дорогим при роботі з великими наборами даних, оскільки потрібна інверсія коваріаційної матриці.
- Вибір функції ядра та її гіперпараметрів може значно вплинути на продуктивність моделі.
Гарні приклади застосування георадара
- Прогноз ціни акцій: Георадар може бути використаний для моделювання та прогнозування цін на акції з урахуванням волатильності та невизначеності на фінансових ринках.
- Комп'ютерні експерименти: Георадар корисний для оптимізації складних симуляцій шляхом моделювання взаємозв’язків вхідних даних і визначення найбільш впливових параметрів.
- Виявлення аномалії: Георадар може бути застосований для виявлення аномалій, коли він визначає незвичайні шаблони в даних часових рядів, фіксуючи нормальний розподіл даних.
Висновок
Підсумовуючи, регресія процесу Гауса є цінним інструментом для аналізу даних і прогнозування в ситуаціях, коли важливо розуміти невизначеність у прогнозах. Використовуючи ймовірнісне моделювання та функції ядра, георадар може надавати точні результати, які можна інтерпретувати. Однак при застосуванні георадара на практиці вкрай важливо враховувати обчислювальні витрати та потребу в експертному внеску.
якщо Редьярд Кіплінг короткий зміст
