Дерево виразів — це дерево, яке використовується для представлення різних виразів. Структура даних дерева використовується для представлення виразних операторів. У цьому дереві внутрішній вузол завжди позначає оператори.
- Листові вузли завжди позначають операнди.
- Операції завжди виконуються над цими операндами.
- Оператор, присутній у глибині дерева, завжди має найвищий пріоритет.
- Оператор, який знаходиться не дуже глибоко в дереві, завжди має найнижчий пріоритет порівняно з операторами, що лежать на глибині.
- Операнд завжди буде присутній на глибині дерева; тому це вважається найвищий пріоритет серед усіх операторів.
- Коротше кажучи, ми можемо підсумувати це як значення, наявне в глибині дерева, має найвищий пріоритет порівняно з іншими операторами, присутніми у верхній частині дерева.
- Основне використання цих дерев виразів полягає в тому, що вони звикли оцінювати, аналізувати і змінювати різні вирази.
- Він також використовується для визначення асоціативності кожного оператора у виразі.
- Наприклад, оператор + є лівоасоціативним, а / – правоасоціативним.
- Дилему цієї асоціативності було знято за допомогою виразу дерева.
- Ці дерева виразів формуються за допомогою контекстно-вільної граматики.
- Ми пов’язали правило в контекстно-вільних граматиках перед кожною граматичною продукцією.
- Ці правила також відомі як семантичні правила, і використовуючи ці семантичні правила, ми можемо легко побудувати дерева виразів.
- Це одна з основних частин проектування компілятора і належить до фази семантичного аналізу.
- У цьому семантичному аналізі ми будемо використовувати переклади, орієнтовані на синтаксис, і у формі вихідних даних створимо анотоване дерево аналізу.
- Анотоване дерево синтаксичного аналізу — це не що інше, як простий синтаксичний аналіз, пов’язаний з атрибутом типу та кожним правилом виробництва.
- Основною метою використання дерев виразів є створення складних виразів, які можна легко обчислити за допомогою цих дерев виразів.
- Воно є незмінним, і коли ми створили дерево виразів, ми не можемо змінити його чи модифікувати далі.
- Щоб внести додаткові зміни, потрібно повністю побудувати нове дерево виразів.
- Він також використовується для розв’язання оцінки виразів постфікса, префікса та інфікса.
Дерева виразів відіграють дуже важливу роль у представленні мовний рівень код у вигляді даних, які в основному зберігаються в деревоподібній структурі. Він також використовується в представленні пам'яті лямбда вираз. Використовуючи структуру даних дерева, ми можемо виразити лямбда-вираз більш прозоро та явно. Спочатку він створюється для перетворення сегмента коду на сегмент даних, щоб можна було легко обчислити вираз.
Дерево виразів — це бінарне дерево, у якому кожен зовнішній або кінцевий вузол відповідає операнду, а кожен внутрішній або батьківський вузол — операторам, тому, наприклад, дерево виразів для 7 + ((1+8)*3) буде таким:
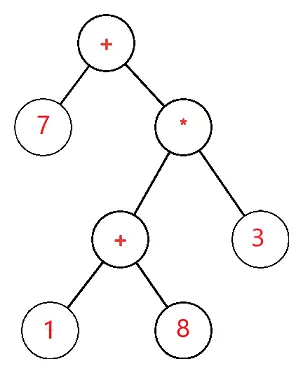
Нехай S — дерево виразів
Якщо S не дорівнює нулю, то
Якщо S.value є операндом, тоді
Повернути S.value
x = вирішити (S.left)
y = вирішити (S.праворуч)
Повернути обчислення (x, y, S.value)
У наведеному вище прикладі дерево виразів використовує контекстно-вільну граматику.
У цій граматиці є деякі постановки, пов’язані з деякими правилами побудови, переважно відомі як семантичні правила . Ми можемо визначити результат, що створює відповідні правила виробництва, використовуючи ці семантичні правила. Тут ми використали параметр значення, який обчислить результат і поверне його до символу початку граматики. S.left обчислить ліву дочірню частину вузла, і аналогічно праву дочірню частину вузла можна обчислити за допомогою параметра S.right.
Використання дерева виразів
- Основною метою використання дерев виразів є створення складних виразів, які можна легко обчислити за допомогою цих дерев виразів.
- Він також використовується для визначення асоціативності кожного оператора у виразі.
- Він також використовується для розв’язання оцінки виразів постфікса, префікса та інфікса.
Реалізація дерева виразів
Щоб реалізувати дерево виразів і написати його програму, нам знадобиться використовувати стекову структуру даних.
Оскільки ми знаємо, що стек заснований на принципі LIFO «останній прийшов, перший вийшов», елемент даних, нещодавно вставлений у стек, виривається, коли це потрібно. Для його реалізації використовуються дві основні операції стека push і pop. Використовуючи операцію push, ми надішлемо елемент даних у стек, а використовуючи операцію pop, ми видалимо елемент даних зі стеку.
Основні функції стека в реалізації дерева виразів:
Перш за все, ми зробимо сканування заданого виразу в порядку зліва направо, потім один за одним перевіримо ідентифікований символ,
- Якщо сканований символ є операндом, ми застосуємо операцію push і помістимо його в стек.
- Якщо відсканований символ є оператором, ми застосуємо до нього операцію pop, щоб видалити два значення зі стеку, щоб зробити їх дочірніми, а потім повернемо поточний батьківський вузол у стек.
Реалізація дерева виразів мовою програмування C
// C program for expression tree implementation #include #include /* The below structure node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ struct node { char info ; struct node* l ; struct node* r ; struct node* nxt ; }; struct node *head=NULL; /* Helper function that allocates a new node with the given data and NULL left and right pointers. */ struct node* newnode(char data) { struct node* node = (struct node*) malloc ( sizeof ( struct node ) ) ; node->info = data ; node->l = NULL ; node->r = NULL ; node->nxt = NULL ; return ( node ) ; } void Inorder(struct node* node) { if ( node == NULL) return ; else { /* first recur on left child */ Inorder ( node->l ) ; /* then print the data of node */ printf ( '%c ' , node->info ) ; /* now recur on right child */ Inorder ( node->r ) ; } } void push ( struct node* x ) { if ( head == NULL ) head = x ; else { ( x )->nxt = head ; head = x ; } // struct node* temp ; // while ( temp != NULL ) // { // printf ( ' %c ' , temp->info ) ; // temp = temp->nxt ; // } } struct node* pop() { // Poping out the top most [pointed with head] element struct node* n = head ; head = head->nxt ; return n ; } int main() { char t[] = { 'X' , 'Y' , 'Z' , '*' , '+' , 'W' , '/' } ; int n = sizeof(t) / sizeof(t[0]) ; int i ; struct node *p , *q , *s ; for ( i = 0 ; i <n ; i++ ) { if read character is operator then popping two other elements from stack and making a binary tree ( t[i]="=" '+' || '-' '*' ' '^' s="newnode" t [ i ] p="pop()" q="pop()" s->l = q ; s->r = p; push(s); } else { s = newnode ( t [ i ] ) ; push ( s ) ; } } printf ( ' The Inorder Traversal of Expression Tree: ' ) ; Inorder ( s ) ; return 0 ; } </n> Вихід наведеної вище програми:
X + Y * Z / W
Реалізація дерева виразів мовою програмування C++
// C++ program for expression tree #include using namespace std ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class node { public: char info ; node* l ; node* r ; node* nxt = NULL ; node ( char c ) { this->info = c ; l = NULL ; r = NULL ; } node() { l = NULL ; r = NULL ; } friend class Stack ; friend class tree ; } ; class Stack { node* head = NULL ; public: void push ( node* ) ; node* pop() ; friend class tree ; } ; class tree { public: void inorder ( node* x ) { // cout<<'tree in inorder traversal is: '<l ) ; cout <info <r } void stack::push( node* x { if ( head="=" null we are inserting here nodes at the top of stack [following lifo principle] else x->nxt = head ; head = x ; } } node* Stack::pop() { // Poping out the top most [ pointed with head ] element node* p = head ; head = head->nxt ; return p ; } int main() { string str = 'XYZ*+W/' ; // If you wish take input from user: //cout << 'Insert Postorder Expression: ' <> s; Stack s ; tree t ; node *p, *q, *re; int n = str.length() ; for ( int i = 0 ; i <n ; i++ ) { if ( str[ i ]="=" '+' || '-' '*' ' '^') re="new" node( str[i] p="s.pop()" q="s.pop()" re->l = q ; re->r = p ; s.push(re) ; } else { re = new node( str[ i ] ) ; s.push(re) ; } } cout << ' The Inorder Traversal of Expression Tree: ' ; t.inorder(re) ; return 0 ; } </n></'tree> Вихід наведеної вище програми:
X + Y * Z / W
Реалізація дерева виразів мовою програмування Java
// Java program for expression tree import java.util.* ; /* The below class node is defined as a node of a binary tree consists of left child and the right child, along with the pointer next which points to the next node */ class Node { char info ; Node l , r ; public Node(char data) { this.info = data ; l = null ; r = null ; } } public class Main { public static boolean isOperator ( char ch ) { if ( ch == '+' || ch == '-' || ch == '*' || ch == '/' || ch == '^' ) { return true ; } return false ; } public static Node Tree ( String postfix ) { Stack st = new Stack(); Node t1,t2,temp ; for ( int i = 0 ; i <p> <strong>The output of the above program is:</strong> </p> <pre> X + Y * Z / W </pre> <hr> 