Кодер — це цифрова схема, яка перетворює набір двійкових вхідних даних в унікальний двійковий код. Двійковий код представляє позицію введення та використовується для ідентифікації конкретного введення, яке є активним. Кодери зазвичай використовуються в цифрових системах для перетворення паралельного набору вхідних даних у послідовний код.
Основним принципом кодера є призначення унікального двійкового коду кожному можливому входу. Наприклад, рядковий кодер 2 до 4 має 2 вхідні лінії та 4 вихідні лінії та призначає унікальний 4-бітовий двійковий код кожній із 2^2 = 4 можливих вхідних комбінацій. Вихід кодера зазвичай має активний низький рівень, тобто лише один вихід активний (низький) у будь-який момент часу, а решта виходів неактивні (високий). Активний низький вихід вибирається на основі двійкового коду, призначеного активному входу.
Існують різні типи кодерів, включаючи кодери пріоритету, які призначають пріоритет кожному входу, і двійково-зважені кодери, які використовують двійкову систему зважування для призначення двійкових кодів входам. Таким чином, кодер — це цифрова схема, яка перетворює набір двійкових вхідних даних в унікальний двійковий код, який представляє позицію вхідних даних. Кодери широко використовуються в цифрових системах для перетворення паралельних входів у послідовні коди.
Кодер - це a комбінаційна схема який виконує операцію, зворотну a Декодер . Він має максимум 2^n вхідних рядків і 'n' вихідних рядків , отже, він кодує інформацію з 2^n входів у n-розрядний код. Він створить двійковий код, еквівалентний вхідному сигналу, який є активним High. Таким чином, кодер кодує 2^n вхідних рядків з «n» бітами.
Кодувальник
Типи кодерів
Існують різні типи кодерів, які згадуються нижче.
- Кодер 4 до 2
- Кодер з вісімкової системи в двійковий (кодер з 8 до 3)
- Десятковий кодер до BCD
- Пріоритетний кодер
Кодер 4 до 2
Кодер 4 до 2 складається з чотири входи Y3, Y2, Y1 & Y0 і два виходи A1 & A0 . У будь-який час лише один із цих 4 входів може бути «1», щоб отримати відповідний двійковий код на виході. На малюнку нижче показано логічний символ кодера 4 до 2.
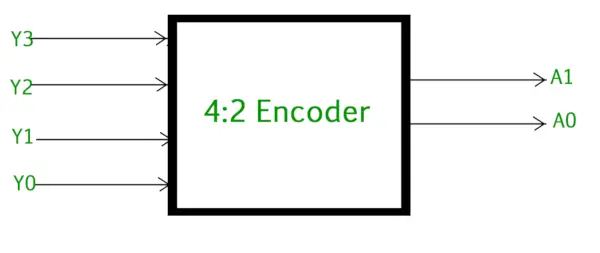
Кодер 4 до 2
numpy linspace
Таблиця істинності від 4 до 2 кодерів виглядає наступним чином.
| ВХОДИ | ВИХОДИ | ||||
|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 |
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
Логічний вираз для A1 і A0:
A1 = Y3 + Y2 A0 = Y3 + Y1>
Наведені вище дві булеві функції A1 і A0 можна реалізувати за допомогою двох вхідних елементів АБО:
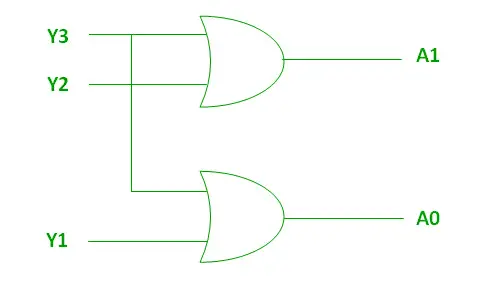
Реалізація за допомогою OR Gate
Кодер з вісімкової системи в двійковий кодер (кодер від 8 до 3)
Кодер 8 до 3 або кодер вісімкового у двійковий складається з 8 входів : Y7 до Y0 і 3 виходи : A2, A1 і A0. Кожен вхідний рядок відповідає кожній вісімковій цифрі, а три виходи генерують відповідний двійковий код. На малюнку нижче показано логічний символ вісімкового кодування двійкового кодера.
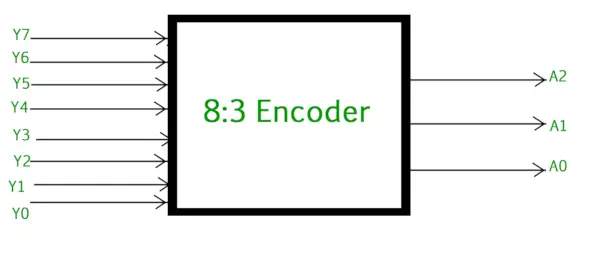
Кодер з вісімкової системи в двійковий кодер (кодер від 8 до 3)
Таблиця істинності для кодера 8 до 3 така.
| ВХОДИ | ВИХОДИ | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Логічний вираз для A2, A1 і A0.
A2 = Y7 + Y6 + Y5 + Y4 A1 = Y7 + Y6 + Y3 + Y2 A0 = Y7 + Y5 + Y3 + Y1>
Наведені вище дві булеві функції A2, A1 і A0 можна реалізувати за допомогою чотирьох входів АБО ворота .
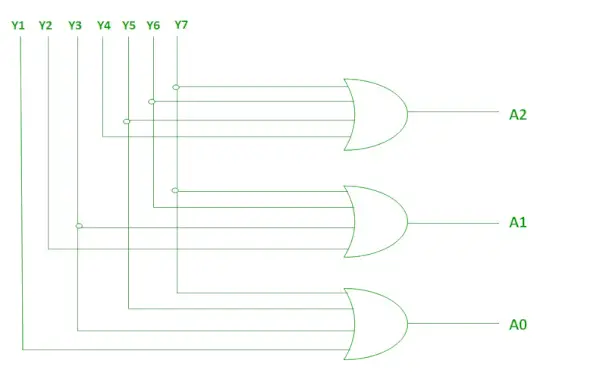
Реалізація за допомогою OR Gate
Десятковий кодер до BCD
Десятково-двійковий кодер зазвичай складається з 10 рядків введення і 4 вихідні рядки . Кожен вхідний рядок відповідає кожній десятковій цифрі, а 4 вихідних – коду BCD. Цей кодер приймає декодовані десяткові дані як вхідні дані та кодує їх у вихід BCD, який доступний на вихідних лініях. На малюнку нижче показано логічний символ кодера від десяткової дроби до BCD:
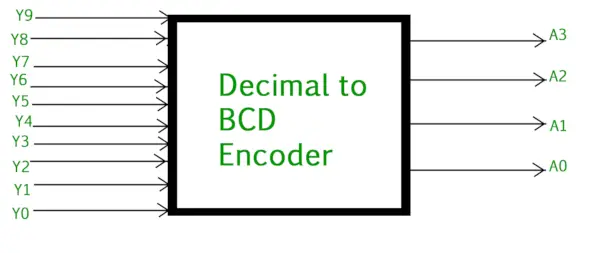
Десятковий кодер до BCD
Таблиця істинності для десяткового до Кодер BCD полягає в наступному.
| ВХОДИ | ВИХОДИ | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Y9 | Y8 | Y7 | Y6 | Y5 | Y4 | Y3 | Y2 | Y1 | Y0 | A3 | A2 | A1 | A0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Логічний вираз для A3, A2, A1 і A0.
A3 = Y9 + Y8 A2 = Y7 + Y6 + Y5 +Y4 A1 = Y7 + Y6 + Y3 +Y2 A0 = Y9 + Y7 +Y5 +Y3 + Y1>
Наведені вище дві булеві функції можна реалізувати за допомогою вентилів АБО.
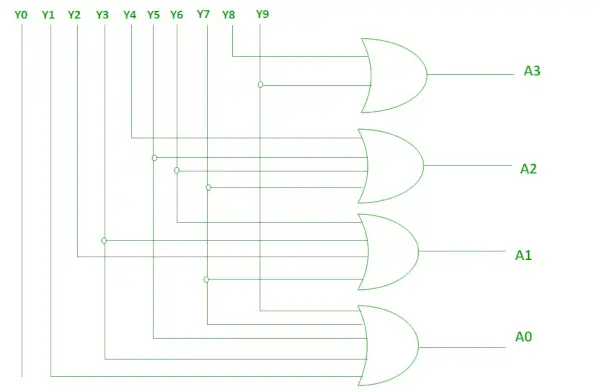
Реалізація за допомогою OR Gate
Пріоритетний кодер
Кодувальник пріоритету 4 до 2 має 4 входи : Y3, Y2, Y1 & Y0 і 2 виходи : A1 і A0. Тут вхід, Y3 має найвищий пріоритет , тоді як вхід Y0 має найнижчий пріоритет . У цьому випадку, навіть якщо кілька вхідних даних є «1» одночасно, виходом буде (двійковий) код, відповідний вхідному сигналу, який має вищий пріоритет . Таблиця істинності для пріоритетного кодера така.
| ВХОДИ | ВИХОДИ | |||||
|---|---|---|---|---|---|---|
| Y3 | Y2 | Y1 | Y0 | A1 | A0 | IN |
| 0 | 0 | 0 | 0 | X | X | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | X | 0 | 1 | 1 |
| 0 | 1 | X | X | 1 | 0 | 1 |
| 1 | X | X | X | 1 | 1 | 1 |
Логічний вираз для A1 показано нижче.
pothineni ram
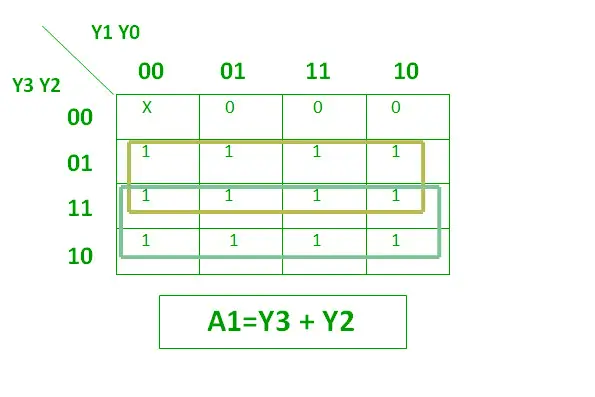
Логічний вираз
Логічний вираз для A0 показано нижче.
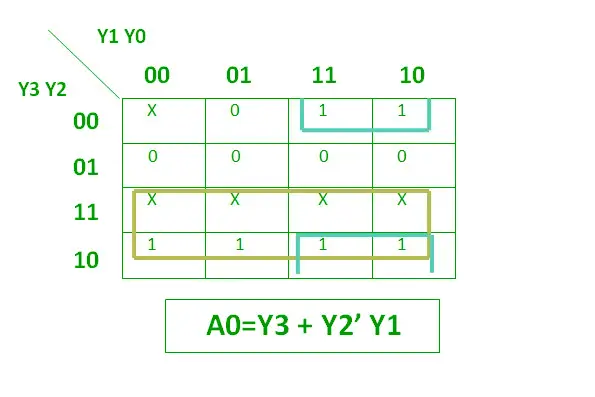
Логічний вираз
Наведені вище дві булеві функції можна реалізувати як.
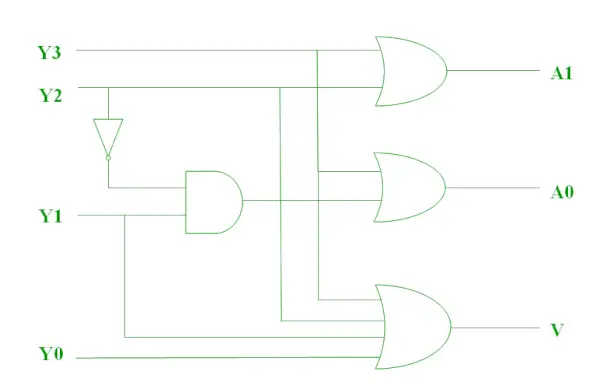
Пріоритетний кодер
Деякі помилки, які зазвичай трапляються в кодувальниках, згадуються нижче.
- Виникає неоднозначність, коли всі виходи кодера дорівнюють нулю.
- Якщо більше ніж один вхід активний високий, то кодер створює вихідний сигнал, який може бути не правильним кодом.
Отже, щоб подолати ці труднощі, ми повинні призначити пріоритети кожному входу кодера. Тоді на виході кодера буде код, що відповідає активним високим входам, які мають вищий пріоритет.
Застосування кодувальників
- Кодери — це дуже поширені електронні схеми, які використовуються в усіх цифрових системах.
- Кодери використовуються для перекладу десяткових значень у двійкові для виконання двійкових функцій, таких як додавання, віднімання, множення тощо.
- Інші програми, особливо для пріоритетних кодерів, можуть включати виявлення переривань у мікропроцесорних програмах.
Переваги використання кодувальників у цифровій логіці
- Зменшення кількості ліній: Кодери зменшують кількість ліній, необхідних для передачі інформації з кількох входів на один вихід, що може спростити конструкцію системи та знизити вартість компонентів.
- Підвищена надійність: Перетворюючи кілька вхідних даних в один серійний код, кодери можуть зменшити ймовірність помилок при передачі інформації.
- Покращена продуктивність: Кодери можуть підвищити продуктивність цифрової системи за рахунок скорочення часу, необхідного для передачі інформації з кількох входів на один вихід.
Недоліки використання кодувальників у цифровій логіці
- Підвищена складність: Кодери зазвичай є складнішими схемами порівняно з мультиплексори , а для реалізації потрібні додаткові компоненти.
- Обмежено конкретними програмами: Кодери підходять лише для програм, де паралельний набір вхідних даних потрібно перетворити на послідовний код.
- Обмежена гнучкість: Кодери обмежені у своїй гнучкості, оскільки вони можуть кодувати лише фіксовану кількість входів у фіксовану кількість виходів.
- Підсумовуючи, кодери — це корисні цифрові схеми, які мають свої переваги та недоліки. Вибір того, використовувати кодер чи ні, залежить від конкретних вимог системи та компромісів між складністю, надійністю, продуктивністю та вартістю.
GATE CS Corner Questions
Відпрацювання наступних запитань допоможе вам перевірити свої знання. Усі запитання ставилися в GATE в попередні роки або в GATE Mock Tests. Настійно рекомендується практикувати їх.
- GATE CS 2013, питання 65
- GATE CS 2014 (набір 3), питання 65
