Видалення вузла з дерева AVL подібне до видалення в бінарному дереві пошуку. Видалення може порушити фактор балансу дерева AVL, тому дерево потрібно повторно збалансувати, щоб зберегти AVLness. Для цього нам потрібно виконувати обертання. Два типи обертання: L-обертання та R-обертання. Тут ми обговоримо R обертання. L поворотів є їх дзеркальним відображенням.
Якщо вузол, який потрібно видалити, присутній у лівому піддереві критичного вузла, тоді необхідно застосувати обертання L, якщо вузол, який потрібно видалити, присутній у правому піддереві критичного вузла. , буде застосовано обертання R.
Розглянемо, що A є критичним вузлом, а B є кореневим вузлом його лівого піддерева. Якщо вузол X, присутній у правому піддереві A, потрібно видалити, то можуть виникнути три різні ситуації:
Обертання R0 (вузол B має коефіцієнт балансу 0)
Якщо вузол B має коефіцієнт балансу 0, а коефіцієнт балансу вузла A порушено після видалення вузла X, тоді дерево буде повторно збалансовано обертанням дерева з використанням обертання R0.
Критичний вузол A переміщується праворуч, а вузол B стає коренем дерева з T1 як його лівим піддеревом. Піддерева T2 і T3 стають лівим і правим піддеревом вузла A. Процес, залучений до обертання R0, показано на наступному зображенні.
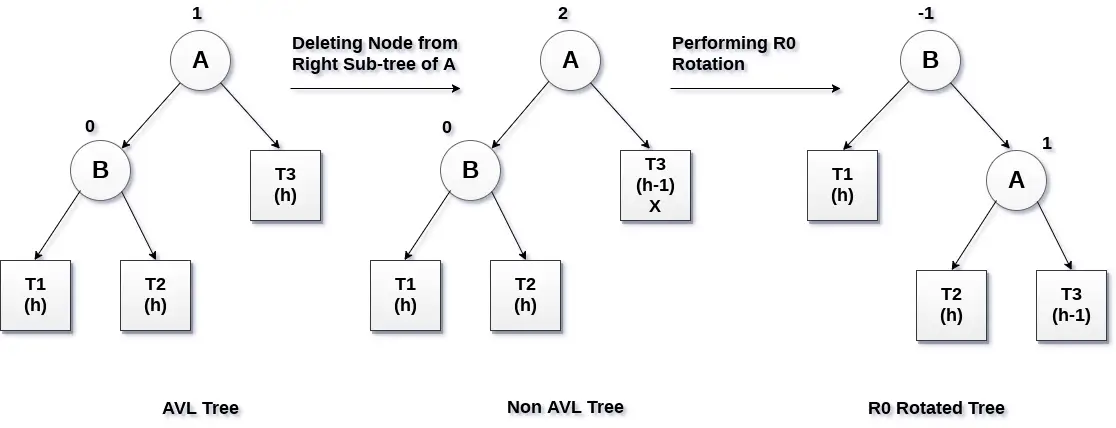
приклад:
Видаліть вузол 30 із дерева AVL, показаного на наступному зображенні.

Рішення
У цьому випадку вузол B має коефіцієнт балансу 0, тому дерево обертатиметься за допомогою обертання R0, як показано на наступному зображенні. Вузол B(10) стає коренем, а вузол A переміщується вправо. Правий нащадок вузла B тепер стане лівим нащадком вузла A.
java привіт світ

Обертання R1 (вузол B має коефіцієнт балансу 1)
Обертання R1 має виконуватися, якщо коефіцієнт балансу вузла B дорівнює 1. Під час обертання R1 критичний вузол A переміщується праворуч, маючи піддерева T2 і T3 як лівий і правий дочірні елементи відповідно. T1 слід розмістити як ліве піддерево вузла B.
Процес обертання R1 показано на наступному зображенні.

приклад
Видаліть вузол 55 із дерева AVL, показаного на наступному зображенні.
перемикач java

рішення:
Видалення 55 з дерева AVL порушує фактор балансу вузла 50, тобто вузла A, який стає критичним вузлом. Це умова обертання R1, за якої вузол A буде переміщено вправо (показано на зображенні нижче). Справа від B тепер стала лівою від A (тобто 45).
Процес, задіяний у розв’язанні, показаний на наступному зображенні.

Обертання R-1 (вузол B має коефіцієнт балансу -1)
Обертання R-1 необхідно виконувати, якщо вузол B має коефіцієнт балансу -1. Цей випадок розглядається так само, як обертання LR. У цьому випадку вузол C, який є правим дочірнім вузлом вузла B, стає кореневим вузлом дерева з B і A як його лівим і правим дочірніми елементами відповідно.
Піддерева T1, T2 стають лівим і правим піддеревами B, тоді як T3, T4 стають лівим і правим піддеревами A.
Процес обертання R-1 показано на наступному зображенні.

приклад
Видаліть вузол 60 із дерева AVL, показаного на наступному зображенні.

рішення:
у цьому випадку вузол B має коефіцієнт балансу -1. Видалення вузла 60 порушує коефіцієнт балансу вузла 50, отже, його потрібно повернути R-1. Вузол C, тобто 45, стає коренем дерева з вузлом B(40) і A(50) як його лівим і правим дочірніми елементами.

