ФОРМУЛА КОТАНГЕНСА

Тригонометрія — важлива галузь математики, яка вивчає співвідношення між довжинами сторін і кутами прямокутного трикутника. Синус, косинус, тангенс, косеканс, секанс і котангенс — це шість тригонометричних співвідношень або функцій. Де тригонометричне співвідношення зображено як співвідношення між сторонами прямокутного трикутника.

sin θ = протилежна сторона/гіпотенуза
cos θ = прилегла сторона/гіпотенуза
tan θ = протилежна сторона/прилегла сторона
cosec θ = 1/sin θ = гіпотенуза/протилежна сторона
сек θ = 1/cos θ = гіпотенуза/прилегла сторона
ліжечко θ = 1/tan θ = сусідня сторона/протилежна сторона

Функція Котангенс є функцією, оберненою до даної функції тангенса. Значення котангенса кута в прямокутному трикутнику дорівнює відношенню довжини сторони, прилеглої до даного кута, до довжини сторони, протилежної даному куту. Котангенс запишемо як cot.

Трикутник ABC

Тепер формула котангенса для кута θ є,

ліжечко θ = (сусідня сторона)/(протилежна сторона)

Функція котангенса додатна в першому і третьому квадрантах і від’ємна в другому і четвертому квадрантах.

cot (2π + θ) = cot θ (1^вулквадрант)
cot (π – θ) = – cot θ (2^ndквадрант)
cot (π + θ) = cot θ (3^rdквадрант)
cot (2π – θ) = – cot θ (4^тисквадрант)

Котангенс є від’ємною функцією, оскільки котангенс від’ємного кута є від’ємним значенням котангенса додатного кута.

cot (-θ) = – cot θ

З точки зору функції тангенса, функція котангенса записується як

ліжечко θ = 1/tan θ

(або)

cot θ = tan (90° – θ) (або) tan (π/2 – θ)

Функцію котангенса через функції синуса та косинуса можна записати як

cot θ = cos θ/sin θ

Ми знаємо, що cot θ = сусідня/протилежна сторона

Тепер розділіть чисельник і знаменник на гіпотенузу

⇒ cot θ = (сусідня сторона/гіпотенуза) / (протилежна сторона/гіпотенуза)

Ми знаємо, що sin θ = протилежна сторона/гіпотенуза

cos θ = прилегла сторона/гіпотенуза

Отже, cot θ = cos θ/sin θ

Функцію котангенса в термінах функції синуса можна записати як

cot θ = (√1 – sin ² i)/sin i

Ми знаємо, що cot θ = cos θ/sin θ

З піфагорійських тотожностей ми маємо;

cos²θ + sin²θ = 1

⇒ cos θ = √1 – sin²i

Отже, cot θ = $frac{sqrt{left(1-sin^{2} heta ight)}}{sin heta}$

Функцію котангенса в термінах функції косинуса можна записати як

cot θ = cos θ/(√1 -cos ² я)

Ми знаємо, що cot θ = cos θ/sin θ
arraylist в java

З піфагорійських тотожностей ми маємо;

cos²θ + sin²θ = 1

sin θ = √1 – cos²i

Отже, cot θ = $frac{cos heta}{sqrt{left(1-cos^{2} heta ight)}}$

Функцію котангенса в термінах секансу та косекансу можна записати як

cot θ = cosec θ/sec θ
Команда повернення java

Ми маємо cot θ = cos θ/sin θ

Це можна записати як cot θ = (1/sin θ) / (1/cos θ)

⇒ cot θ = cosec θ/sec θ

Функцію котангенса через косеканс можна записати так:

cot θ = √(cosec ² - 1)

З тотожностей Піфагора ми маємо,

cosec²θ – ліжечко²θ = 1

⇒ ліжечко²θ = 1 – cosec²- 1

Отже, cot θ = √(cosec²- 1)

Функцію котангенса в термінах функції січної можна записати так:

cot θ = 1/(√сек ² я – 1)

З тотожностей Піфагора ми маємо,

сек²θ – отже²θ = 1

tan θ = √сек²я – 1

Ми знаємо, що cot θ = 1/tan θ

Отже, ліжечко θ = $frac{1}{sqrt{left(1-sec^{2} heta ight)}}$

Таблиця тригонометричного співвідношення

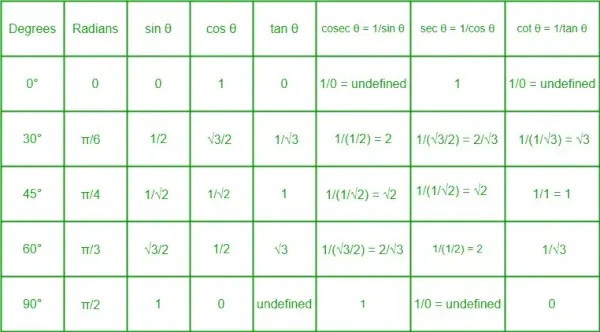
Таблиця тригонометричного співвідношення

Закон котангенса або закон котангенса

Закон котангенса виглядає схожим на закон синуса, але тут він містить половини кутів. Закон котангенсів описує співвідношення між довжинами сторін трикутника та котангенсами половин трьох кутів. Розглянемо трикутник ABC, де a, b і c — довжини сторін трикутника.

Закон котангенсів стверджує, що

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Де s — півпериметр трикутника ABC, а r — його внутрішній радіус вписаного кола трикутника.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Зразки завдань

Задача 1: Знайдіть значення cot θ, якщо tan θ = 3/4.

рішення:

Наведені дані, tan θ = 3/4

ми це знаємо, ліжечко θ = 1/tan θ

⇒ ліжечко θ = 1/(3/4) = 4/3

Отже, cot θ = 4/3

Задача 2: Знайдіть значення cot α, sin α = 1/3 і cos α = 2√2/3.

рішення:

За даними sin α = 1/3 і cos α = 2√2/3

ми це знаємо, cot α = cos α/sin α

⇒ ліжечко α = (2√2/3) / (1/3) = 2√2

Отже, значення cot α = 2√2

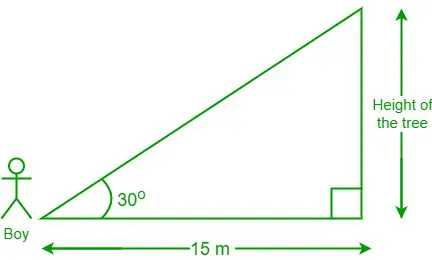
Задача 3: Хлопчик, який стоїть на відстані 15 м від дерева, дивиться на верхівку дерева під кутом 30 градусів. Яка висота дерева?

рішення:

Діаграма з наведених даних

За даними, відстань між хлопчиком і підніжжям дерева = 15 м і θ = 30°

Нехай висота дерева буде «h»

Ми маємо, ліжечко θ = сусідня/протилежна сторона

⇒ ліжечко 30° = 15/год

⇒ √3 = 15/год [оскільки ліжечко 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 м

Отже, висота дерева = 5√3 м

Задача 4: Знайдіть значення cot x, якщо sec x = 6/5.

рішення:

прокручування мишею не працює

Дані дані, сек х = 6/5

Ми маємо, сек ² х – отже ² х = 1

⇒ (6/5)²- так²х = 1

⇒ 36/25 – так²х = 1

⇒ так²х = 36/25 – 1
види машинного навчання

⇒ так²х = 11/25

⇒ tan x = √(11/25) = √11/5

ми це знаємо, ліжечко x = 1/тен x

⇒ ліжечко x = 1/(√11/5) = 5/√11

Отже, cot x = 5/√11

Задача 5: Знайдіть значення cot θ, якщо cosec θ = 25/24.

рішення:

За даними cosec θ = 25/24

ми це знаємо, cot θ = √(cosec ² - 1)

⇒ ліжечко θ = √(25/24)²- 1

⇒ ліжечко θ =√(625 – 576)/576 = √49/576

⇒ ліжечко θ = 7/24

Отже, значення cot θ = 7/24

Задача 6: Знайдіть значення cot β, якщо sin β = 5/13.

рішення:

За даними sin β = 5/13

ми це знаємо, без ² β + cos ² β = 1

⇒ (5/13)²+ cos²β = 1

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

cot β = cosβ/sin β

= (12/13) / (5/13)

⇒ ліжечко β = 12/5

Отже, значення cot β = 12/5
alter додати стовпець oracle

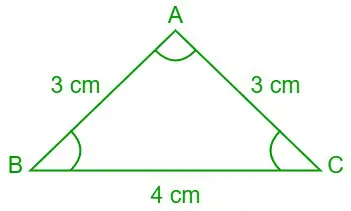
Завдання 7. Використовуючи закон котангенсів, знайдіть значення ∠A, ∠B і ∠C (у градусах), якщо довжини трьох сторін трикутника ABC дорівнюють a = 4 см, b= 3 см і c= 3 см.

рішення:

Дано a = 4 см, b = 3 см і c = 3 см

Трикутник ABC

З закону котангенсів,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Тепер s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

Радіус трикутника r = 2/√5

З рівняння закону котангенсів,

ліжечко (A/2)/1 = 1/(2/√5)

⇒ ліжечко (A/2) = √5/2 ⇒ A/2 = ліжечко^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

ліжечко (B/2)/2 = 1/(2/√5)

⇒ ліжечко (B/2)/2 = √5/2 ⇒ ліжечко (B/2) = √5

⇒ (B/2) = ліжечко^-1(√5) = 24,1° ⇒ ∠B = 48,2°

ліжечко (C/2)/2 = 1/(2/√5)

⇒ cot(C/2) = √5 ⇒ (C/2) = cot^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Отже, кути трикутника ABC дорівнюють ∠A = 83,6°, ∠B = 48,2° і ∠C = 48,2°.